青岛版六三制六年级上册五完美的图形——圆信息窗3 圆和环形的面积课件(34张PPT)
文档属性
| 名称 | 青岛版六三制六年级上册五完美的图形——圆信息窗3 圆和环形的面积课件(34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-07 17:16:02 | ||
图片预览






文档简介
青岛版数学
六年级上册
圆和环形的面积
青岛版数学六年级(上)
五 完美的图形
——圆
通过操作、观察,引导学生推导出圆和环形的面积计算公式,并能运用公式解决实际问题。
培养观察、分析、推理和概括的能力,发展空间观念。
在圆面积计算公式的推导过程中,体会转化思想和极限思想。
【重点】
掌握圆和环形的面积计算公式,会用公式解题。
【难点】
圆的面积计算公式的推导。
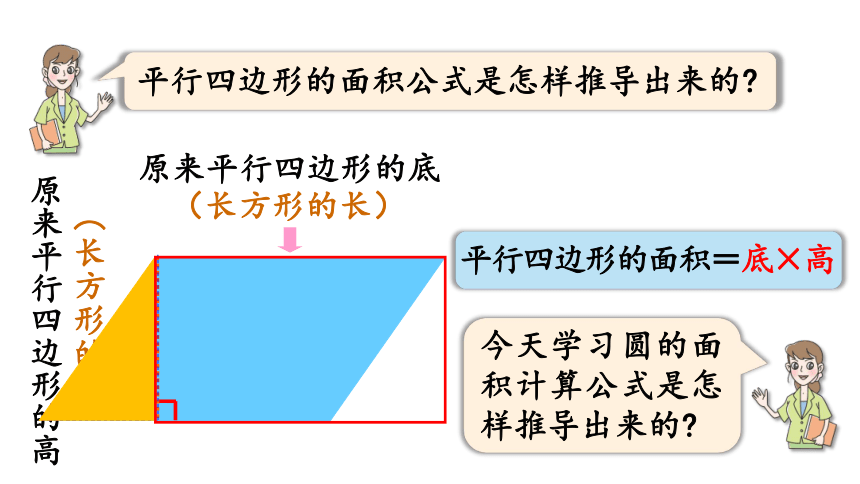
平行四边形的面积公式是怎样推导出来的?
平行四边形的面积=底×高
原来平行四边形的底
原来平行四边形的高
(长方形的长)
(长方形的宽)
今天学习圆的面积计算公式是怎样推导出来的?
2008年北京奥运会闭幕式圆形中心舞台的直径是20米,其中有一个直径是1.6米的圆形升降舞台。
你能提出什么问题?
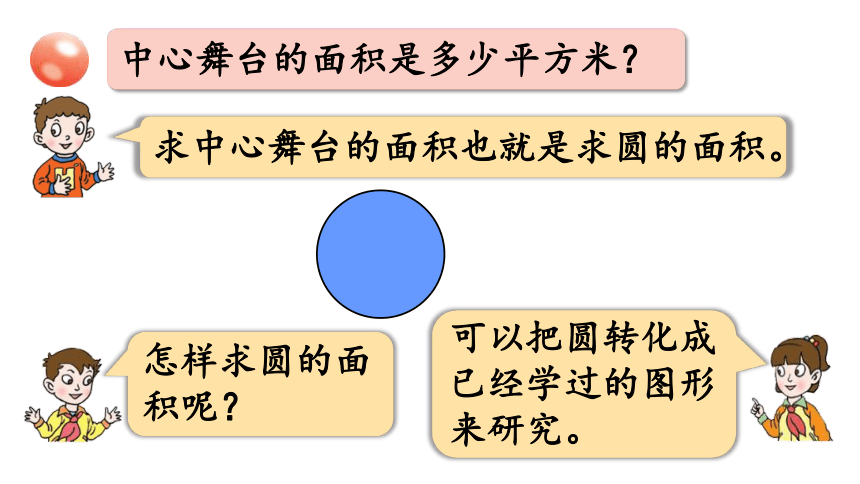
中心舞台的面积是多少平方米?
求中心舞台的面积也就是求圆的面积。
怎样求圆的面积呢?
可以把圆转化成已经学过的图形来研究。
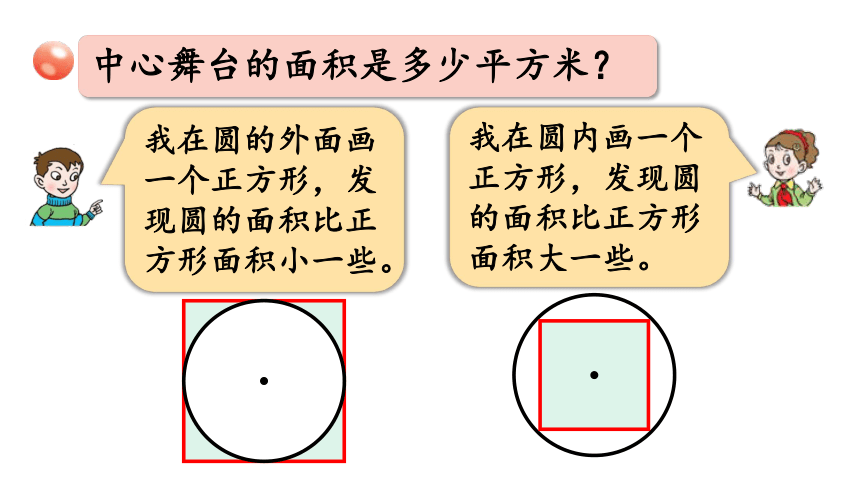
中心舞台的面积是多少平方米?
我在圆的外面画一个正方形,发现圆的面积比正方形面积小一些。
我在圆内画一个正方形,发现圆的面积比正方形面积大一些。
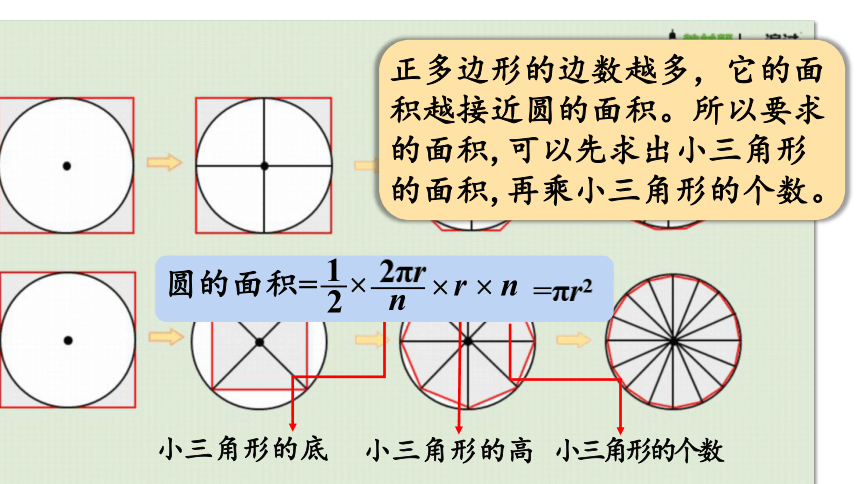
圆的面积=
1
2
2πr
?
n
×
×
×
r
n
=πr2
?
小三角形的底
小三角形的高
小三角形的个数
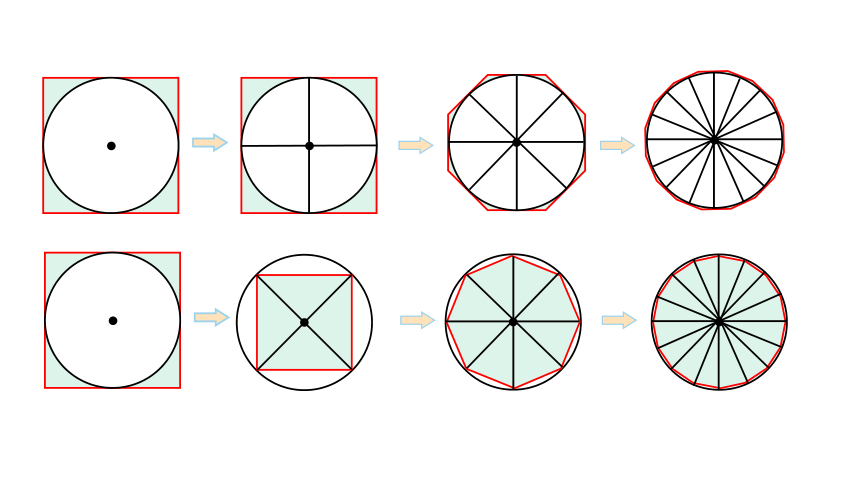
正多边形的边数越多,它的面积越接近圆的面积。所以要求的面积,可以先求出小三角形的面积,再乘小三角形的个数。
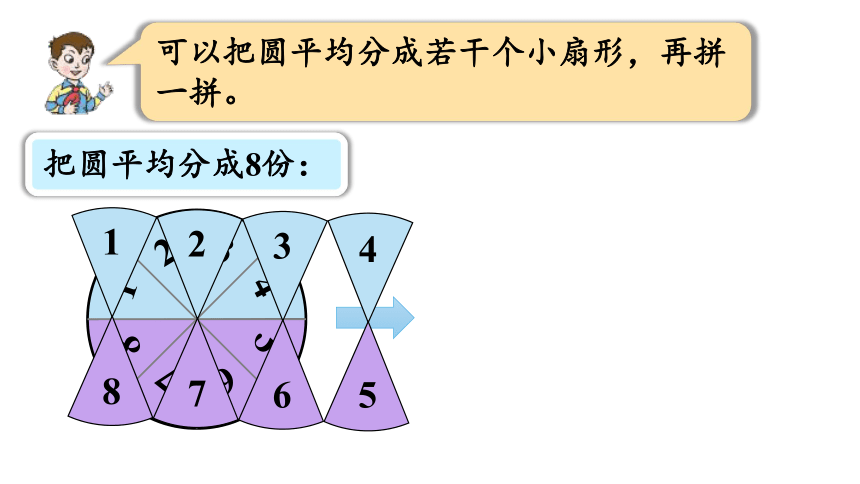
可以把圆平均分成若干个小扇形,再拼一拼。
把圆平均分成8份:
1
2
3
4
5
6
7
8
2
1
4
3
7
8
5
6
可以把圆平均分成若干个小扇形,再拼一拼。
把圆平均分成16份:
1
2
3
4
5
6
7
8
16
15
14
13
12
11
10
9
1
2
3
4
5
6
7
8
16
15
14
13
12
11
10
9
可以把圆平均分成若干个小扇形,再拼一拼。
把圆平均分成32份:
可以把圆平均分成若干个小扇形,再拼一拼。
平均分成8份:
平均分成16份:
平均分成32份:
有点像平行四边形,但是有两条边是曲线。
更像平行四边形,但是有两条边是曲线。
近似的长方形
可以把圆平均分成若干个小扇形,再拼一拼。
我发现平均分的份数越多,拼成的图形越接近于长方形。
拼成的长方形与原来的圆形之间有怎样的关系?
r
r
C
1
2
拼成的长方形的面积等于圆的面积。
r
C
1
2
长方形的面积
=
长
×
宽
圆的面积
=
C
1
2
×
r
=
1
2
×
2πr
×
r
πr?
=
如果用S表示圆的面积,那么圆的面积计算公式可以写成:
S=πr?
中心舞台的面积是多少平方米?
答:中心舞台的面积是314平方米。
= 3.14×102
= 3.14×100
= 314(平方米)
3.14×
( )2
20
2
2008年北京奥运会闭幕式圆形中心舞台的直径是20米,其中有一个直径是1.6米的圆形升降舞台。
下面图形的面积是多少平方厘米?
12厘米
20厘米
这个图形是环形。
求环形面积,可以用外圆面积减去内圆面积。
S=πR? - πr?或S=π(R? - r?)
下面图形的面积是多少平方厘米?
答:这个图形的面积是200.96平方厘米。
= 3.14×100 - 3.14×36
= 200.96(平方厘米)
3.14×
( )2
20
2
12厘米
20厘米
-
3.14×
( )2
12
2
= 3.14×102
- 3.14×62
= 314-113.04
答:升降舞台的面积大约是2平方米。
= 3.14×1.62
= 3.14×0.64
= 2.0096(平方米)
3.14×
( )2
1.6
2
2.0096平方米≈2平方米
2008年北京奥运会闭幕式圆形中心舞台中有一个直径是1.6米的圆形升降舞台。升降舞台的面积大约是多少平方米?(得数保留整数)
1
3.14×82
= 3.14×64
= 200.96(平方米)
答:喷灌面积是200.96平方米。
(教材第68页“自主练习”第3题 )
喷灌面积就是半径为8米的圆的面积。
这个自动旋转喷水器的喷灌面积是多少平方米?
2
(教材第68页“自主练习”第5题 )
2m
3m
2m
S=πr?
=3.14×1?
=3.14(m?)
长方形中切割一个最大的圆,圆的直径是长方形的宽。
(2)3×2=6(m?)
6-3.14=2.86(m?)
答:圆的面积是3.14平方米,剩余部分的面积是2.86平方米。
(1) 2÷2=1(m)
用一张长方形铁板(如右图)切割出一个最大的圆。
(1)圆的面积是多少平方米?
(2)剩余部分的面积是多少平方米?
3
{35758FB7-9AC5-4552-8A53-C91805E547FA}半径
(cm)
直径
(cm)
周长
(cm)
圆的面积
(cm2)
3
8
9.42
6
18.84
28.26
4
25.12
50.24
3
1.5
7.065
(教材第68页“自主练习”第6题 )
将表格补充完整。
4
10dm
40cm
(教材第69页“自主练习”第8题节选 )
计算下面各图涂色部分的面积。
5
(教材第69页“自主练习”第8题节选 )
10dm
=3.14×25÷2
半圆面积:
3.14× ( 10÷2 ) 2÷2
=39.25 (平方分米)
三角形面积:
10×5÷2=25 (平方分米)
39.25-25=14.25(平方分米)
涂色部分面积:
计算下面各图涂色部分的面积。
5
(教材第69页“自主练习”第8题节选 )
=3.14×400
圆面积:
3.14× ( 40÷2 ) 2
=1256 (平方厘米)
正方形面积:
40×40=1600 (平方厘米)
1600-1256=344(平方厘米)
涂色部分面积:
40cm
计算下面各图涂色部分的面积。
5
(教材第69页“自主练习”第10题 )
增加的面积就是环形的面积。
30m
5m
扩建前面积:
3.14× ( 30÷2 ) 2
= 706.5(平方米)
= 3.14×152
3.14× ( 30÷2+5 ) 2
= 1256 (平方米)
扩建后面积:
= 3.14×202
1256-706.5 = 549.5(平方米)
答:扩建后旱冰场的面积增加了549.5平方米。
一个圆形旱冰场的直径是30米,扩建后半径增加了5米。扩建后旱冰场的面积增加了多少平方米?
6
圆所占平面的大小叫作圆的面积。
圆的面积= 圆周率×半径的平方
我知道了圆面积的意义及其计算公式。
同学们,这节课你们学会了哪些知识?
S=πr?
环形是两个半径不相等的同心圆之间的部分。
环形的面积= 大圆的面积 -小圆的面积
S=πR? - πr?或S=π(R? - r?)
我知道了环形的意义及其面积的计算公式。
同学们,这节课你们学会了哪些知识?
相关练习。
02
01
自主练习第1、2、4、11题。
六年级上册
圆和环形的面积
青岛版数学六年级(上)
五 完美的图形
——圆
通过操作、观察,引导学生推导出圆和环形的面积计算公式,并能运用公式解决实际问题。
培养观察、分析、推理和概括的能力,发展空间观念。
在圆面积计算公式的推导过程中,体会转化思想和极限思想。
【重点】
掌握圆和环形的面积计算公式,会用公式解题。
【难点】
圆的面积计算公式的推导。
平行四边形的面积公式是怎样推导出来的?
平行四边形的面积=底×高
原来平行四边形的底
原来平行四边形的高
(长方形的长)
(长方形的宽)
今天学习圆的面积计算公式是怎样推导出来的?
2008年北京奥运会闭幕式圆形中心舞台的直径是20米,其中有一个直径是1.6米的圆形升降舞台。
你能提出什么问题?
中心舞台的面积是多少平方米?
求中心舞台的面积也就是求圆的面积。
怎样求圆的面积呢?
可以把圆转化成已经学过的图形来研究。
中心舞台的面积是多少平方米?
我在圆的外面画一个正方形,发现圆的面积比正方形面积小一些。
我在圆内画一个正方形,发现圆的面积比正方形面积大一些。
圆的面积=
1
2
2πr
?
n
×
×
×
r
n
=πr2
?
小三角形的底
小三角形的高
小三角形的个数
正多边形的边数越多,它的面积越接近圆的面积。所以要求的面积,可以先求出小三角形的面积,再乘小三角形的个数。
可以把圆平均分成若干个小扇形,再拼一拼。
把圆平均分成8份:
1
2
3
4
5
6
7
8
2
1
4
3
7
8
5
6
可以把圆平均分成若干个小扇形,再拼一拼。
把圆平均分成16份:
1
2
3
4
5
6
7
8
16
15
14
13
12
11
10
9
1
2
3
4
5
6
7
8
16
15
14
13
12
11
10
9
可以把圆平均分成若干个小扇形,再拼一拼。
把圆平均分成32份:
可以把圆平均分成若干个小扇形,再拼一拼。
平均分成8份:
平均分成16份:
平均分成32份:
有点像平行四边形,但是有两条边是曲线。
更像平行四边形,但是有两条边是曲线。
近似的长方形
可以把圆平均分成若干个小扇形,再拼一拼。
我发现平均分的份数越多,拼成的图形越接近于长方形。
拼成的长方形与原来的圆形之间有怎样的关系?
r
r
C
1
2
拼成的长方形的面积等于圆的面积。
r
C
1
2
长方形的面积
=
长
×
宽
圆的面积
=
C
1
2
×
r
=
1
2
×
2πr
×
r
πr?
=
如果用S表示圆的面积,那么圆的面积计算公式可以写成:
S=πr?
中心舞台的面积是多少平方米?
答:中心舞台的面积是314平方米。
= 3.14×102
= 3.14×100
= 314(平方米)
3.14×
( )2
20
2
2008年北京奥运会闭幕式圆形中心舞台的直径是20米,其中有一个直径是1.6米的圆形升降舞台。
下面图形的面积是多少平方厘米?
12厘米
20厘米
这个图形是环形。
求环形面积,可以用外圆面积减去内圆面积。
S=πR? - πr?或S=π(R? - r?)
下面图形的面积是多少平方厘米?
答:这个图形的面积是200.96平方厘米。
= 3.14×100 - 3.14×36
= 200.96(平方厘米)
3.14×
( )2
20
2
12厘米
20厘米
-
3.14×
( )2
12
2
= 3.14×102
- 3.14×62
= 314-113.04
答:升降舞台的面积大约是2平方米。
= 3.14×1.62
= 3.14×0.64
= 2.0096(平方米)
3.14×
( )2
1.6
2
2.0096平方米≈2平方米
2008年北京奥运会闭幕式圆形中心舞台中有一个直径是1.6米的圆形升降舞台。升降舞台的面积大约是多少平方米?(得数保留整数)
1
3.14×82
= 3.14×64
= 200.96(平方米)
答:喷灌面积是200.96平方米。
(教材第68页“自主练习”第3题 )
喷灌面积就是半径为8米的圆的面积。
这个自动旋转喷水器的喷灌面积是多少平方米?
2
(教材第68页“自主练习”第5题 )
2m
3m
2m
S=πr?
=3.14×1?
=3.14(m?)
长方形中切割一个最大的圆,圆的直径是长方形的宽。
(2)3×2=6(m?)
6-3.14=2.86(m?)
答:圆的面积是3.14平方米,剩余部分的面积是2.86平方米。
(1) 2÷2=1(m)
用一张长方形铁板(如右图)切割出一个最大的圆。
(1)圆的面积是多少平方米?
(2)剩余部分的面积是多少平方米?
3
{35758FB7-9AC5-4552-8A53-C91805E547FA}半径
(cm)
直径
(cm)
周长
(cm)
圆的面积
(cm2)
3
8
9.42
6
18.84
28.26
4
25.12
50.24
3
1.5
7.065
(教材第68页“自主练习”第6题 )
将表格补充完整。
4
10dm
40cm
(教材第69页“自主练习”第8题节选 )
计算下面各图涂色部分的面积。
5
(教材第69页“自主练习”第8题节选 )
10dm
=3.14×25÷2
半圆面积:
3.14× ( 10÷2 ) 2÷2
=39.25 (平方分米)
三角形面积:
10×5÷2=25 (平方分米)
39.25-25=14.25(平方分米)
涂色部分面积:
计算下面各图涂色部分的面积。
5
(教材第69页“自主练习”第8题节选 )
=3.14×400
圆面积:
3.14× ( 40÷2 ) 2
=1256 (平方厘米)
正方形面积:
40×40=1600 (平方厘米)
1600-1256=344(平方厘米)
涂色部分面积:
40cm
计算下面各图涂色部分的面积。
5
(教材第69页“自主练习”第10题 )
增加的面积就是环形的面积。
30m
5m
扩建前面积:
3.14× ( 30÷2 ) 2
= 706.5(平方米)
= 3.14×152
3.14× ( 30÷2+5 ) 2
= 1256 (平方米)
扩建后面积:
= 3.14×202
1256-706.5 = 549.5(平方米)
答:扩建后旱冰场的面积增加了549.5平方米。
一个圆形旱冰场的直径是30米,扩建后半径增加了5米。扩建后旱冰场的面积增加了多少平方米?
6
圆所占平面的大小叫作圆的面积。
圆的面积= 圆周率×半径的平方
我知道了圆面积的意义及其计算公式。
同学们,这节课你们学会了哪些知识?
S=πr?
环形是两个半径不相等的同心圆之间的部分。
环形的面积= 大圆的面积 -小圆的面积
S=πR? - πr?或S=π(R? - r?)
我知道了环形的意义及其面积的计算公式。
同学们,这节课你们学会了哪些知识?
相关练习。
02
01
自主练习第1、2、4、11题。
