江西省抚州市2020-2021学年高二下学期期末考试数学(文)试题 Word版含答案解析
文档属性
| 名称 | 江西省抚州市2020-2021学年高二下学期期末考试数学(文)试题 Word版含答案解析 |

|
|
| 格式 | docx | ||
| 文件大小 | 915.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-07 00:00:00 | ||
图片预览




文档简介
抚州市2020-2021学年高二下学期期末考试
数学·B卷(文科)
考生注意:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分。考试时间120分钟。
2.请将各题答案填写在答题卡上。
3.本试卷主要考试内容:北师大版选修1-1第四章,1-2,4-4,4-5,集合,函数。
第Ⅰ卷
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合false,false,则false( )
A.false B.false C.false D.false
2.复数false的虚部为( )
A.2 B.false C.false D.false
3.下面给出的类比推理中(其中false为实数集.false为复数集),结论正确的是( )
A.由“已知false,false,若false,则false”类比推出“已知false,false,若false,则a=士b”
B.由“若直线false,false,false满足false,false,则false”类比推出“若向量false,false,false满足false,false,则false
C.由“已知false,false,若false,则false”类比推出“已知false,false,若false,则false”
D.由“平面向量false满足false”类比推出“空间向量false满足false”
4.某篮球运动员投篮的命中率为0.8,现投了5次球,则5次都没投中的概率为( )
A.false B.false C.0.8 D.0.2
5.用反证法证明“连续的自然数false,false,false中至少有一个奇数”,假设正确的是( )
A.false,false,false中至多有一个奇数 B.false,false,false都是奇数
C.false,false,false中至少有两个奇数 D.false,false,false都是偶数
6.已知函数false,若false,则false的取值范围为( )
A.false B.false C.false D.false
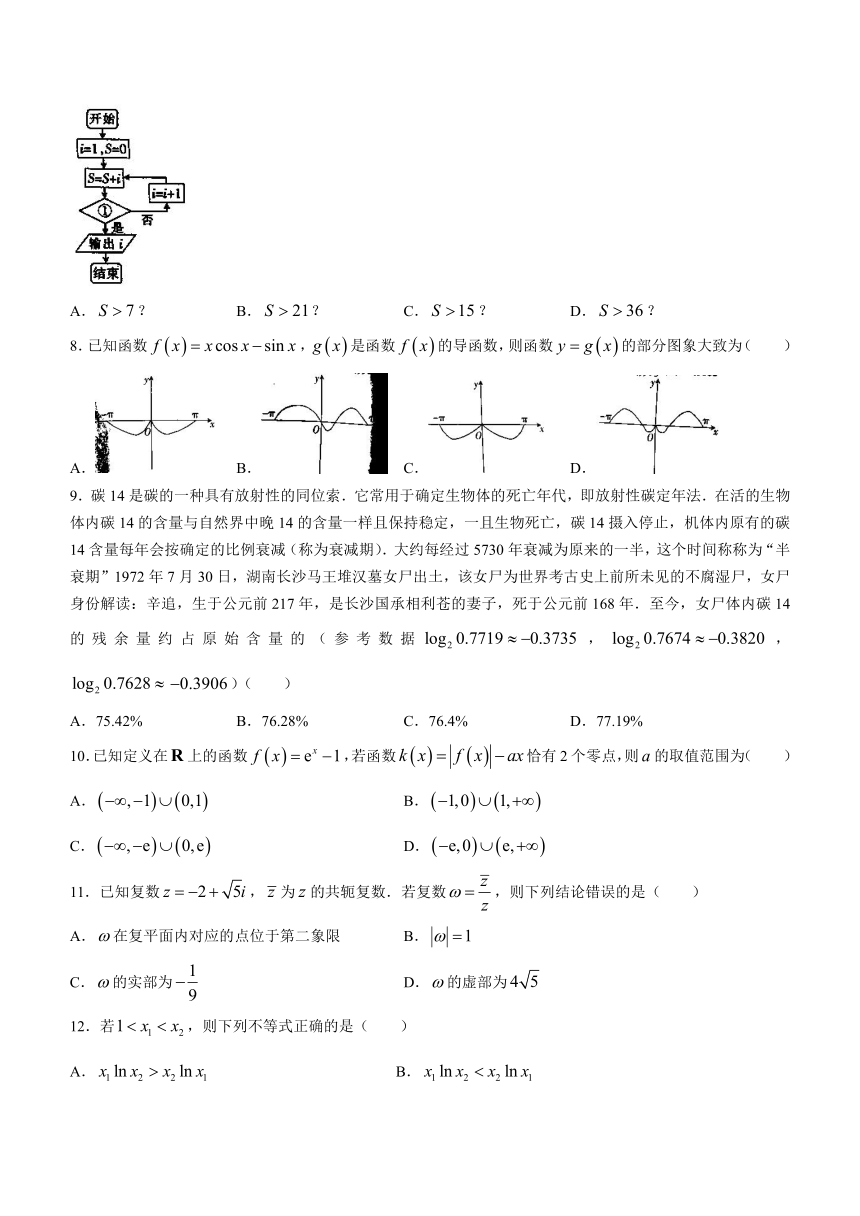
7.执行如图所示的程序框图,若输出false的值为6,则框图中①处可以填入( )
A.false? B.false? C.false? D.false?
8.已知函数false,false是函数false的导函数,则函数false的部分图象大致为( )
A. B. C. D.
9.碳14是碳的一种具有放射性的同位索.它常用于确定生物体的死亡年代,即放射性碳定年法.在活的生物体内碳14的含量与自然界中晚14的含量一样且保持稳定,一且生物死亡,碳14摄入停止,机体内原有的碳14含量每年会按确定的比例衰减(称为衰减期).大约每经过5730年衰减为原来的一半,这个时间称称为“半衰期”1972年7月30日,湖南长沙马王堆汉墓女尸出土,该女尸为世界考古史上前所未见的不腐湿尸,女尸身份解读:辛追,生于公元前217年,是长沙国承相利苍的妻子,死于公元前168年.至今,女尸体内碳14的残余量约占原始含量的(参考数据false,false,falsefalse)( )
A.75.42% B.76.28% C.76.4% D.77.19%
10.已知定义在false上的函数false,若函数false恰有2个零点,则false的取值范围为( )
A.false B.false
C.false D.false11.已知复数false,false为false的共轭复数.若复数false,则下列结论错误的是( )
A.false在复平面内对应的点位于第二象限 B.false
C.false的实部为false D.false的虚部为false
12.若false,则下列不等式正确的是( )
A.false B.false
C.false D.false
第Ⅱ卷
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置.
13.若false,则false的实部为______.
14.某同学数学成绩及格的概率是0.8,优秀的概率是0.6,已知在某次数学检测中该同学成绩及格了,则该同学此次检测成绩优秀的概率是______.
15.已知false,false,则false______.
16.毕达哥拉斯学派是由古希腊哲学家毕达哥拉斯及其信徒组成的学派,他们把美学视为自然科学的一个组成部分.美表现在数量比例上的对称与和谐,和谐起于差异的对立,美的本质在于和谐.他们常把数描绘成沙滩上的沙粒或小石子,并由它们排列而成的形状对自然数进行研究如图所示,图形的点数分别为1.5,2,22,…总结规律并以此类推下去,第8个图形对应的点数为______,若这些数构成一个数列,记为数列false,则false______.(本题第一空2分,第二空3分)
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每道试题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.(12分)
某网站的调查显示,健身操类、跑步类、拉伸运动类等健身项目在大众健康项目中比较火热,但是大多数人对健身科学类的知识相对缺乏,尤其是健身指导方面.现从某健身房随机抽取50名会员,其中男生有20人,对其平均每天健身的时间进行调查,并根据日均健身时间分为false,false,false,false,false五组,得到如图所示的男生日均健身时间频数表与女生日均健身时间频率分布直方图.规定日均健身时间不少于60分钟的人为“喜欢健身”。
男生日均健身时间频数表:
日均健身时间(分钟)
false
false
false
false
false
人数
2
6
6
4
2
(1)请完成下面的false列联表.
喜欢健身
不喜欢健身
总计
男生
女生
总计
根据以上的false列联表,能否有95%的把握认为喜欢健身与性别有关?
(2)现从日均健身时间在false的学员中选取3人进行表彰,求选取的3人中至少有1名男生的概率.
附:false,其中false.
false
0.05
0.025
0.01
0.005
false
3.841
5.024
6.635
7.829
18.(12分)
已知函数false.
(1)求曲线false在点false处的切线方程;
(2)设函数false,求false的定义域和值域。
19.(12分)
已知函数false,false.
(1)求false的单调区间;
(2)若false,false,false,求false的取值范围.
20.(12分)
自从新型冠状病毒爆发以来,美国疫情持续升级,下表是美国2020年4月9日~12月14日每隔25天统计1次共统计1次的累计确诊人数(单位:万)表.
日期(月/日)
4/09
5/04
5/29
6/23
7/18
8/12
9/06
10/01
10/26
11/20
12/15
统计时间顺序false
1
2
3
4
5
6
7
8
9
10
11
累计确诊人数false
43.3
118.8
179.4
238.8
377.0
536.0
646.0
744.7
888.9
1187.4
1673.7
将4月9日作为第一次统计,若将统计时间顺序作为变量false,每次累计确诊人数作为变量false,给出两个函数模型:①false,②false.
令false,对上表的数据作初步处理,得到部分数据已作近似处理的一些统计量的参考值.false,false,false,false,false,false,取false,false,false,false,false.
(1)已知模型②false的相关系数false,试判断模型①相比较②哪一个更适合作为false与false的回归方程,并说明理由;
(2)根据(1)的结果及以上数据,求false与false的回归方程(精确到0.01,每一步用上一步的近似值进行解答);
(3)经过医学研究,发现新型冠状病毒有易传染.一个病毒的携带者在病情发作之前通常有长达14天的潜伏期,这个期间如果不采取防护措施,则感染者与一位健康者接触时间超过15秒就有可能传染病毒.根据(2)求出的回归方程,估计如果不加强防护措施,2021年3月25日美国的累计确诊人数是否会突破6500万.
附:线性回归方程false中,false,false,
相关系数false.
21.(12分)
已知函数false.
(1)若false,求false的取值范围;
(2)若函数false,且关于false的方程false有两个不同的实数根,求false的取值范围.
(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.
22.[选修4-4:坐标系与参数方程](10分)
在直角坐标系false中,圆false的参数方程为false(false为参数),以false为极点,false轴的非负半轴为极轴建立极坐标系.
(1)求圆false的极坐标方程;
(2)直线false的极坐标方程是false,直线false:false与圆false的交点为false,false,与直线false的交点为false,求线段false的长.
23.[选修4-5:不等式选讲](10分)
已知函数false.
(1)当false时,求不等式false的解集;
(2)若false的解集包含false,求false的取值范围.
抚州市2020-2021学年高二下学期期末考试
数学·B卷参考答案(文科)
1.C 因为false,所以false.
2.B false.
3.D 在复数集false中,若两个复数满足false,则只表示它们的模相等,false,false不一定相等或相反,所以A不正确;
当false为零向量,false,false为不共线的非零向量时,不满足向量平行的传递性,所以B不正确;
在复数集false中,例如false,false,此时false,但false,false都是虚数,无法比较大小,所以C不正确;
平面向量或空间向量false,均满足false,所以D正确.
4.A 5次都没投中的概率false.
5.D 因为反证法中的反设就是原命题的否定,所以正确的反设为“false,false,false都是偶数”.
6.B 因为false为false上的偶函数,且在false上单调递增,所以由false,可得false,
解得false.
7.C false,false;false,false;false,false;false,false;false,false;false,false;false,此时根据条件应跳出循环,输出false.所以填入“false?”时符合要求.
8.A false即false,因为false为偶函数,故排除B,又当false时,false,故排除D.因为false,所以false在false处的切线斜率为负数.故选A.
9.C ∵每经过5730年衰减为原来的一半,
∴生物体内碳14的含量false与死亡年数false之间的函数关系式为false.
现在是2021年,所以女尸从死亡至今已有false年,
由题意可得,false.
因为false,所以false.
10.B 观察直线false与曲线false的位置关系,false所以false.
11.D 因为false,所以false,
所以false,
false在复平面内对应的点为false,位于第二象限,false,false的实部是false,虚部是false,所以A,B,C正确,D错误
12.A 构造函数false,则false,又当false时,false,当false时,false,所以false在false上单调递增,在false上单调递减,所以false,false的大小不确定.所以A、B均不正确;构造函数false,则false,所以false在false上为增函数,所以false,即false,所以false.故选D.
13.false ∵false,∴false,故false的实部为false.
14.0.75 记数学成绩及格为事件false,数学成绩优秀为事件false,则false,false,false,所以false.
15.15 由false,得false,false,则false,false.
所以false,所以false.
16.92;336 记第false个图形的点数为false,由题意知false,false,
false,false,…,false,
累加得false,
即false,所以false.又false,
所以false.
17.解:(1)填表如下:
喜欢健身
不喜欢健身
总计
男生
6
14
20
女生
6
24
30
总计
12
38
50
从而false,
故没有95%的把握认为喜欢健身与性别有关.
(2)记3名女生为false,false,false,2名男生为false,false,
则从5人中抽取3人的所有可能情况为false,false,false,false,false,false,false,false,false,false,共10种,
其中3人中至少有1名男生的情况有9种,
所以所求概率false.
18.解:(1)false,false,
则false.
又false,所以曲线false在点false处的切线方程为false,
即false.
(2)由false,得false,
又false,所以false的定义域为false.
因为false,所以false,
所以false,
则false,故false的值域为false.
19.解:(1)false.
在false和false上,false,false单调递增.
在false上,false,false单调递减.
综上,false的单调递增区间为false和false,单调递减区间为false.
(2)由(1)可知,false在false和false上单调递增,在false上单调递减.
又false,false,false,false.
所以在false上,false.
又false.
所以在false上,false,false,
即false.
因为false,false,false,
所以false解得false.
故false的取值范围是false.
20.解:(1)由false,得false,即false.
因为false,
所以false,
所以模型①拟合得更好,更适合作为false与false的回归方程.
(2)因为false,
false,
所以false,
所以回归方程为false.
(3)2021年3月25
日对应的时间序号false,
当false时,false,
所以如果不加强防护措施,2021年3月25日美国的累计确诊人数将会突破6500万.
21.解:(1)false的定义域为false,false等价于false.
令false,false,则false.
当false时,false,false单调递增;当false时,false,false单调递减.
所以false,
所以false,即false的取值范围为false.
(2)由false,可得false.
设false,false,则由题意可知,
false在false上有两个零点,又false.
则当false时,false,false单调递增;当false时,false,false单调递减.
所以false,
因为false在false上有两个零点,所以false,即false.
又false,所以false在false上有且只有一个零点.
由(1)可知,当false时,false,
则false,
所以false在false上有且只有一个零点.
综上,false的取值范围为false.
22.解:(1)圆false的普通方程为false,
又false,false,所以圆false的极坐标方程为false.
(2)设false,则由false解得false,得false;
设false,则由false解得false,得false.
所以false.
23.解:(1)由已知得false.
①当false时,由false,解得false,此时false;
②当false时,由false,解得false,此时false;
③当false时,由false,解得false,此时false.
综上所述,不等式false的解集为false.
(2)由false,可得false.
因为false,所以false,
即false,则false,
所以false,即false的取值范围为false.
数学·B卷(文科)
考生注意:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分。考试时间120分钟。
2.请将各题答案填写在答题卡上。
3.本试卷主要考试内容:北师大版选修1-1第四章,1-2,4-4,4-5,集合,函数。
第Ⅰ卷
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合false,false,则false( )
A.false B.false C.false D.false
2.复数false的虚部为( )
A.2 B.false C.false D.false
3.下面给出的类比推理中(其中false为实数集.false为复数集),结论正确的是( )
A.由“已知false,false,若false,则false”类比推出“已知false,false,若false,则a=士b”
B.由“若直线false,false,false满足false,false,则false”类比推出“若向量false,false,false满足false,false,则false
C.由“已知false,false,若false,则false”类比推出“已知false,false,若false,则false”
D.由“平面向量false满足false”类比推出“空间向量false满足false”
4.某篮球运动员投篮的命中率为0.8,现投了5次球,则5次都没投中的概率为( )
A.false B.false C.0.8 D.0.2
5.用反证法证明“连续的自然数false,false,false中至少有一个奇数”,假设正确的是( )
A.false,false,false中至多有一个奇数 B.false,false,false都是奇数
C.false,false,false中至少有两个奇数 D.false,false,false都是偶数
6.已知函数false,若false,则false的取值范围为( )
A.false B.false C.false D.false
7.执行如图所示的程序框图,若输出false的值为6,则框图中①处可以填入( )
A.false? B.false? C.false? D.false?
8.已知函数false,false是函数false的导函数,则函数false的部分图象大致为( )
A. B. C. D.
9.碳14是碳的一种具有放射性的同位索.它常用于确定生物体的死亡年代,即放射性碳定年法.在活的生物体内碳14的含量与自然界中晚14的含量一样且保持稳定,一且生物死亡,碳14摄入停止,机体内原有的碳14含量每年会按确定的比例衰减(称为衰减期).大约每经过5730年衰减为原来的一半,这个时间称称为“半衰期”1972年7月30日,湖南长沙马王堆汉墓女尸出土,该女尸为世界考古史上前所未见的不腐湿尸,女尸身份解读:辛追,生于公元前217年,是长沙国承相利苍的妻子,死于公元前168年.至今,女尸体内碳14的残余量约占原始含量的(参考数据false,false,falsefalse)( )
A.75.42% B.76.28% C.76.4% D.77.19%
10.已知定义在false上的函数false,若函数false恰有2个零点,则false的取值范围为( )
A.false B.false
C.false D.false11.已知复数false,false为false的共轭复数.若复数false,则下列结论错误的是( )
A.false在复平面内对应的点位于第二象限 B.false
C.false的实部为false D.false的虚部为false
12.若false,则下列不等式正确的是( )
A.false B.false
C.false D.false
第Ⅱ卷
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置.
13.若false,则false的实部为______.
14.某同学数学成绩及格的概率是0.8,优秀的概率是0.6,已知在某次数学检测中该同学成绩及格了,则该同学此次检测成绩优秀的概率是______.
15.已知false,false,则false______.
16.毕达哥拉斯学派是由古希腊哲学家毕达哥拉斯及其信徒组成的学派,他们把美学视为自然科学的一个组成部分.美表现在数量比例上的对称与和谐,和谐起于差异的对立,美的本质在于和谐.他们常把数描绘成沙滩上的沙粒或小石子,并由它们排列而成的形状对自然数进行研究如图所示,图形的点数分别为1.5,2,22,…总结规律并以此类推下去,第8个图形对应的点数为______,若这些数构成一个数列,记为数列false,则false______.(本题第一空2分,第二空3分)
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每道试题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.(12分)
某网站的调查显示,健身操类、跑步类、拉伸运动类等健身项目在大众健康项目中比较火热,但是大多数人对健身科学类的知识相对缺乏,尤其是健身指导方面.现从某健身房随机抽取50名会员,其中男生有20人,对其平均每天健身的时间进行调查,并根据日均健身时间分为false,false,false,false,false五组,得到如图所示的男生日均健身时间频数表与女生日均健身时间频率分布直方图.规定日均健身时间不少于60分钟的人为“喜欢健身”。
男生日均健身时间频数表:
日均健身时间(分钟)
false
false
false
false
false
人数
2
6
6
4
2
(1)请完成下面的false列联表.
喜欢健身
不喜欢健身
总计
男生
女生
总计
根据以上的false列联表,能否有95%的把握认为喜欢健身与性别有关?
(2)现从日均健身时间在false的学员中选取3人进行表彰,求选取的3人中至少有1名男生的概率.
附:false,其中false.
false
0.05
0.025
0.01
0.005
false
3.841
5.024
6.635
7.829
18.(12分)
已知函数false.
(1)求曲线false在点false处的切线方程;
(2)设函数false,求false的定义域和值域。
19.(12分)
已知函数false,false.
(1)求false的单调区间;
(2)若false,false,false,求false的取值范围.
20.(12分)
自从新型冠状病毒爆发以来,美国疫情持续升级,下表是美国2020年4月9日~12月14日每隔25天统计1次共统计1次的累计确诊人数(单位:万)表.
日期(月/日)
4/09
5/04
5/29
6/23
7/18
8/12
9/06
10/01
10/26
11/20
12/15
统计时间顺序false
1
2
3
4
5
6
7
8
9
10
11
累计确诊人数false
43.3
118.8
179.4
238.8
377.0
536.0
646.0
744.7
888.9
1187.4
1673.7
将4月9日作为第一次统计,若将统计时间顺序作为变量false,每次累计确诊人数作为变量false,给出两个函数模型:①false,②false.
令false,对上表的数据作初步处理,得到部分数据已作近似处理的一些统计量的参考值.false,false,false,false,false,false,取false,false,false,false,false.
(1)已知模型②false的相关系数false,试判断模型①相比较②哪一个更适合作为false与false的回归方程,并说明理由;
(2)根据(1)的结果及以上数据,求false与false的回归方程(精确到0.01,每一步用上一步的近似值进行解答);
(3)经过医学研究,发现新型冠状病毒有易传染.一个病毒的携带者在病情发作之前通常有长达14天的潜伏期,这个期间如果不采取防护措施,则感染者与一位健康者接触时间超过15秒就有可能传染病毒.根据(2)求出的回归方程,估计如果不加强防护措施,2021年3月25日美国的累计确诊人数是否会突破6500万.
附:线性回归方程false中,false,false,
相关系数false.
21.(12分)
已知函数false.
(1)若false,求false的取值范围;
(2)若函数false,且关于false的方程false有两个不同的实数根,求false的取值范围.
(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.
22.[选修4-4:坐标系与参数方程](10分)
在直角坐标系false中,圆false的参数方程为false(false为参数),以false为极点,false轴的非负半轴为极轴建立极坐标系.
(1)求圆false的极坐标方程;
(2)直线false的极坐标方程是false,直线false:false与圆false的交点为false,false,与直线false的交点为false,求线段false的长.
23.[选修4-5:不等式选讲](10分)
已知函数false.
(1)当false时,求不等式false的解集;
(2)若false的解集包含false,求false的取值范围.
抚州市2020-2021学年高二下学期期末考试
数学·B卷参考答案(文科)
1.C 因为false,所以false.
2.B false.
3.D 在复数集false中,若两个复数满足false,则只表示它们的模相等,false,false不一定相等或相反,所以A不正确;
当false为零向量,false,false为不共线的非零向量时,不满足向量平行的传递性,所以B不正确;
在复数集false中,例如false,false,此时false,但false,false都是虚数,无法比较大小,所以C不正确;
平面向量或空间向量false,均满足false,所以D正确.
4.A 5次都没投中的概率false.
5.D 因为反证法中的反设就是原命题的否定,所以正确的反设为“false,false,false都是偶数”.
6.B 因为false为false上的偶函数,且在false上单调递增,所以由false,可得false,
解得false.
7.C false,false;false,false;false,false;false,false;false,false;false,false;false,此时根据条件应跳出循环,输出false.所以填入“false?”时符合要求.
8.A false即false,因为false为偶函数,故排除B,又当false时,false,故排除D.因为false,所以false在false处的切线斜率为负数.故选A.
9.C ∵每经过5730年衰减为原来的一半,
∴生物体内碳14的含量false与死亡年数false之间的函数关系式为false.
现在是2021年,所以女尸从死亡至今已有false年,
由题意可得,false.
因为false,所以false.
10.B 观察直线false与曲线false的位置关系,false所以false.
11.D 因为false,所以false,
所以false,
false在复平面内对应的点为false,位于第二象限,false,false的实部是false,虚部是false,所以A,B,C正确,D错误
12.A 构造函数false,则false,又当false时,false,当false时,false,所以false在false上单调递增,在false上单调递减,所以false,false的大小不确定.所以A、B均不正确;构造函数false,则false,所以false在false上为增函数,所以false,即false,所以false.故选D.
13.false ∵false,∴false,故false的实部为false.
14.0.75 记数学成绩及格为事件false,数学成绩优秀为事件false,则false,false,false,所以false.
15.15 由false,得false,false,则false,false.
所以false,所以false.
16.92;336 记第false个图形的点数为false,由题意知false,false,
false,false,…,false,
累加得false,
即false,所以false.又false,
所以false.
17.解:(1)填表如下:
喜欢健身
不喜欢健身
总计
男生
6
14
20
女生
6
24
30
总计
12
38
50
从而false,
故没有95%的把握认为喜欢健身与性别有关.
(2)记3名女生为false,false,false,2名男生为false,false,
则从5人中抽取3人的所有可能情况为false,false,false,false,false,false,false,false,false,false,共10种,
其中3人中至少有1名男生的情况有9种,
所以所求概率false.
18.解:(1)false,false,
则false.
又false,所以曲线false在点false处的切线方程为false,
即false.
(2)由false,得false,
又false,所以false的定义域为false.
因为false,所以false,
所以false,
则false,故false的值域为false.
19.解:(1)false.
在false和false上,false,false单调递增.
在false上,false,false单调递减.
综上,false的单调递增区间为false和false,单调递减区间为false.
(2)由(1)可知,false在false和false上单调递增,在false上单调递减.
又false,false,false,false.
所以在false上,false.
又false.
所以在false上,false,false,
即false.
因为false,false,false,
所以false解得false.
故false的取值范围是false.
20.解:(1)由false,得false,即false.
因为false,
所以false,
所以模型①拟合得更好,更适合作为false与false的回归方程.
(2)因为false,
false,
所以false,
所以回归方程为false.
(3)2021年3月25
日对应的时间序号false,
当false时,false,
所以如果不加强防护措施,2021年3月25日美国的累计确诊人数将会突破6500万.
21.解:(1)false的定义域为false,false等价于false.
令false,false,则false.
当false时,false,false单调递增;当false时,false,false单调递减.
所以false,
所以false,即false的取值范围为false.
(2)由false,可得false.
设false,false,则由题意可知,
false在false上有两个零点,又false.
则当false时,false,false单调递增;当false时,false,false单调递减.
所以false,
因为false在false上有两个零点,所以false,即false.
又false,所以false在false上有且只有一个零点.
由(1)可知,当false时,false,
则false,
所以false在false上有且只有一个零点.
综上,false的取值范围为false.
22.解:(1)圆false的普通方程为false,
又false,false,所以圆false的极坐标方程为false.
(2)设false,则由false解得false,得false;
设false,则由false解得false,得false.
所以false.
23.解:(1)由已知得false.
①当false时,由false,解得false,此时false;
②当false时,由false,解得false,此时false;
③当false时,由false,解得false,此时false.
综上所述,不等式false的解集为false.
(2)由false,可得false.
因为false,所以false,
即false,则false,
所以false,即false的取值范围为false.
同课章节目录
