空间两点间的距离
图片预览



文档简介
(共14张PPT)
一,空间直角坐标系
—Oxyz
横轴
纵轴
竖轴
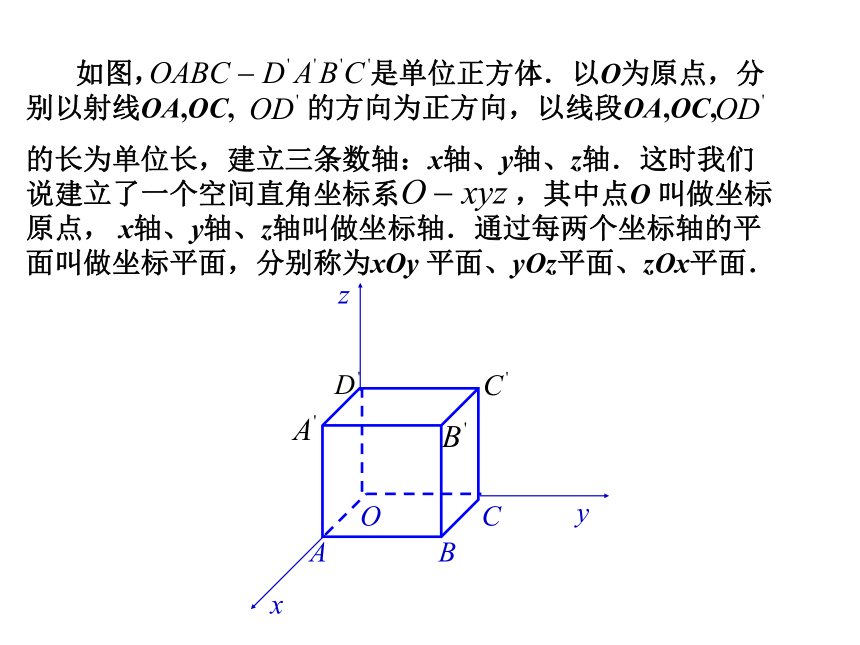
如图, 是单位正方体.以O为原点,分别以射线OA,OC, 的方向为正方向,以线段OA,OC,
的长为单位长,建立三条数轴:x轴、y轴、z轴.这时我们说建立了一个空间直角坐标系 ,其中点O 叫做坐标原点, x轴、y轴、z轴叫做坐标轴.通过每两个坐标轴的平面叫做坐标平面,分别称为xOy 平面、yOz平面、zOx平面.
A
B
C
O
y
x
z
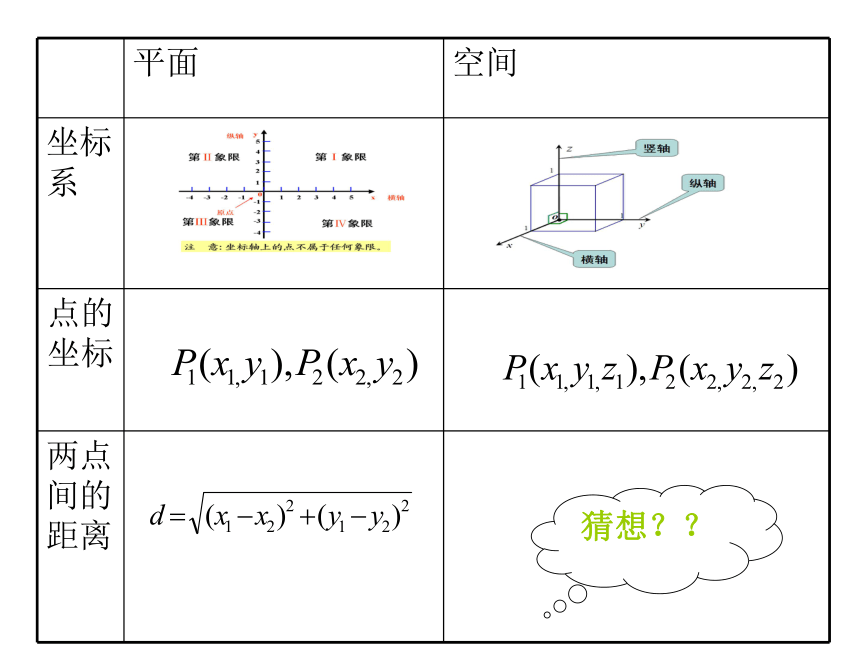
平面 空间
坐标系
点的坐标
两点间的距离
猜想??
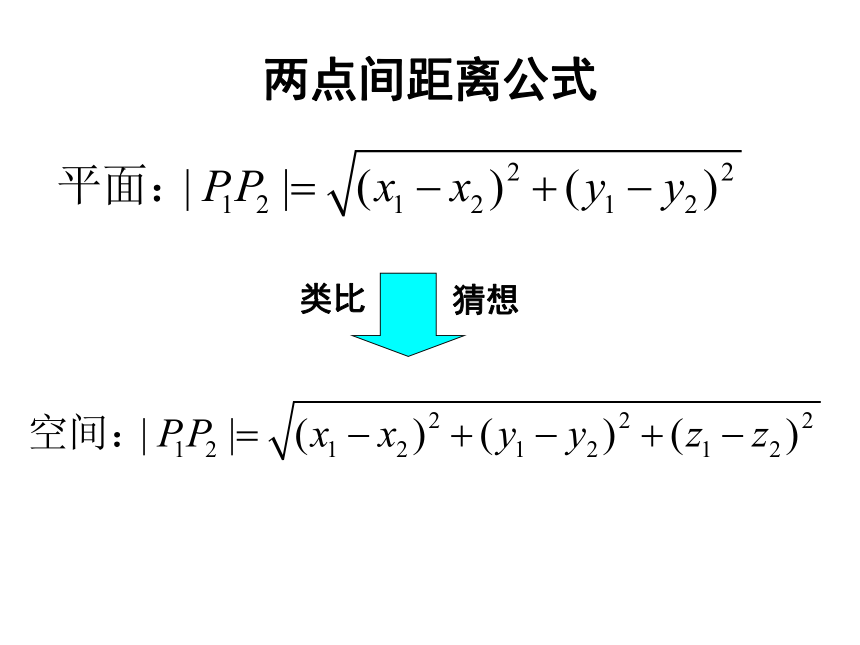
两点间距离公式
类比
猜想
2.3.2 空间两点间的距离
一. 空间两点间的距离公式
z
x
y
O
P(x,y,z)
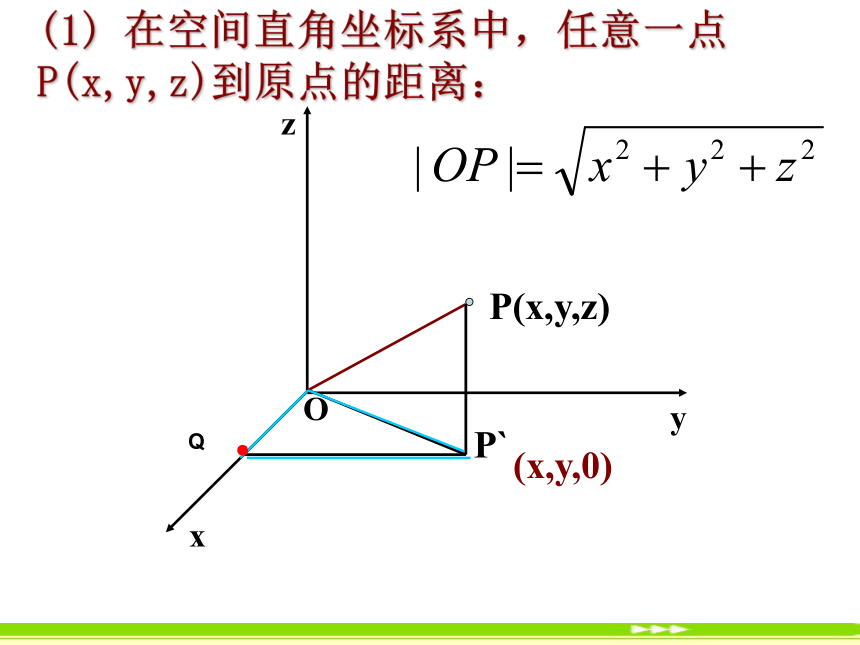
(1) 在空间直角坐标系中,任意一点P(x,y,z)到原点的距离:
P`
(x,y,0)
●
Q
Y
Z
X
O
Q
(2,2,-1)
(5,2,-1)
●
●
●
●
R
Y
Z
X
O
●
●
●
●
Q
R
在空间直角坐标系中,点P(x1,y1,z1)和
点Q(x2,y2,z2)的中点坐标(x,y,z):
二、空间中点坐标公式:
例1:已知三角形的三个顶点A(1,5,2),
B(2,3,4),C(3,1,5),
求:BC边上中线AM的长。
解:
例4:已知 ,在平面Oyz上是否存在一点C,使 为等边三角形,如果存在求C坐标,不存在说明理由。
解:假设存在一点C(0,y,z),满足条件:
例4:已知 ,在平面Oyz上是否存在一点C,使 为等边三角形,如果存在求C坐标,不存在说明理由。
所以存在一点C,满足条件.
一,空间直角坐标系
—Oxyz
横轴
纵轴
竖轴
如图, 是单位正方体.以O为原点,分别以射线OA,OC, 的方向为正方向,以线段OA,OC,
的长为单位长,建立三条数轴:x轴、y轴、z轴.这时我们说建立了一个空间直角坐标系 ,其中点O 叫做坐标原点, x轴、y轴、z轴叫做坐标轴.通过每两个坐标轴的平面叫做坐标平面,分别称为xOy 平面、yOz平面、zOx平面.
A
B
C
O
y
x
z
平面 空间
坐标系
点的坐标
两点间的距离
猜想??
两点间距离公式
类比
猜想
2.3.2 空间两点间的距离
一. 空间两点间的距离公式
z
x
y
O
P(x,y,z)
(1) 在空间直角坐标系中,任意一点P(x,y,z)到原点的距离:
P`
(x,y,0)
●
Q
Y
Z
X
O
Q
(2,2,-1)
(5,2,-1)
●
●
●
●
R
Y
Z
X
O
●
●
●
●
Q
R
在空间直角坐标系中,点P(x1,y1,z1)和
点Q(x2,y2,z2)的中点坐标(x,y,z):
二、空间中点坐标公式:
例1:已知三角形的三个顶点A(1,5,2),
B(2,3,4),C(3,1,5),
求:BC边上中线AM的长。
解:
例4:已知 ,在平面Oyz上是否存在一点C,使 为等边三角形,如果存在求C坐标,不存在说明理由。
解:假设存在一点C(0,y,z),满足条件:
例4:已知 ,在平面Oyz上是否存在一点C,使 为等边三角形,如果存在求C坐标,不存在说明理由。
所以存在一点C,满足条件.
