棱柱、棱锥和棱台
图片预览



文档简介
(共41张PPT)
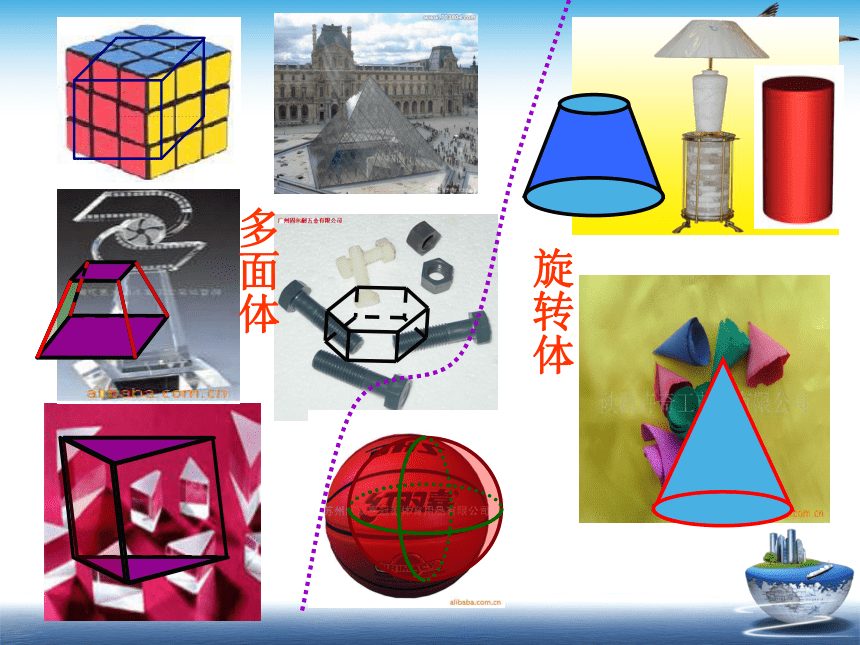
定义:对于空间上的物体,如果我们只考虑它的的形状和大小,而不考虑其他因素(密度,颜色,位置等),从中抽象出来的空间图形叫做空间几何体.
分类:
1.多面体:由若干个平面多边形围成的几何体;
2.旋转体:由一个平面图形绕它所在平面内的一条直线旋转所形成的封闭几何体.
多面体
旋转体
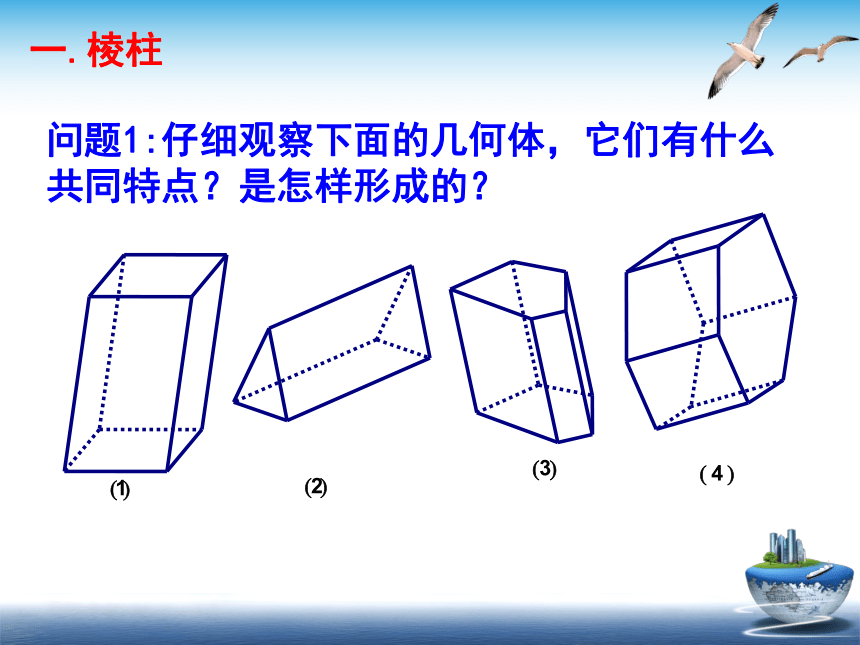
问题1:仔细观察下面的几何体,它们有什么
共同特点?是怎样形成的?
4
(
)
3
(
)
2
(
)
1
(
)
一.棱柱
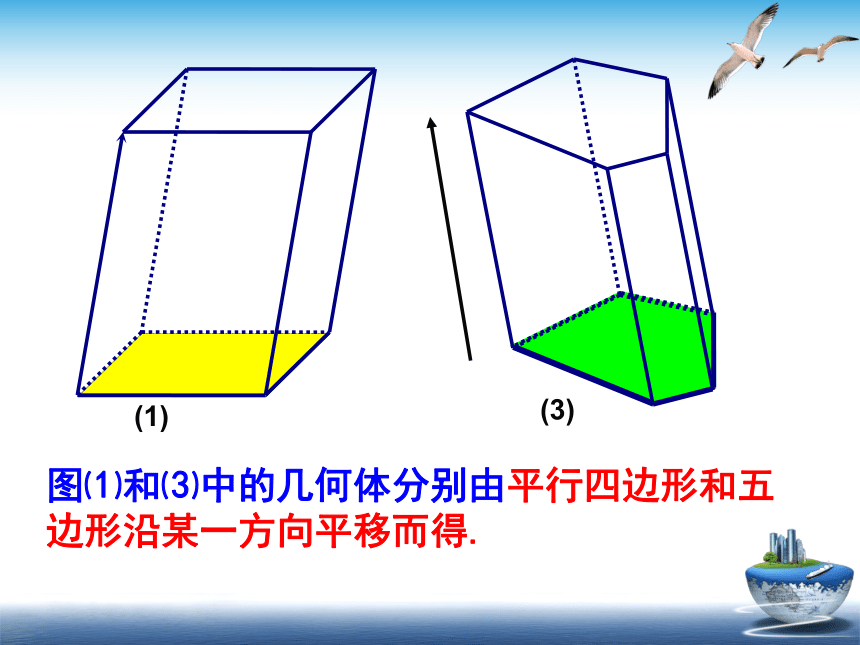
图⑴和⑶中的几何体分别由平行四边形和五
边形沿某一方向平移而得.
(1)
(3)
⑵
⑷
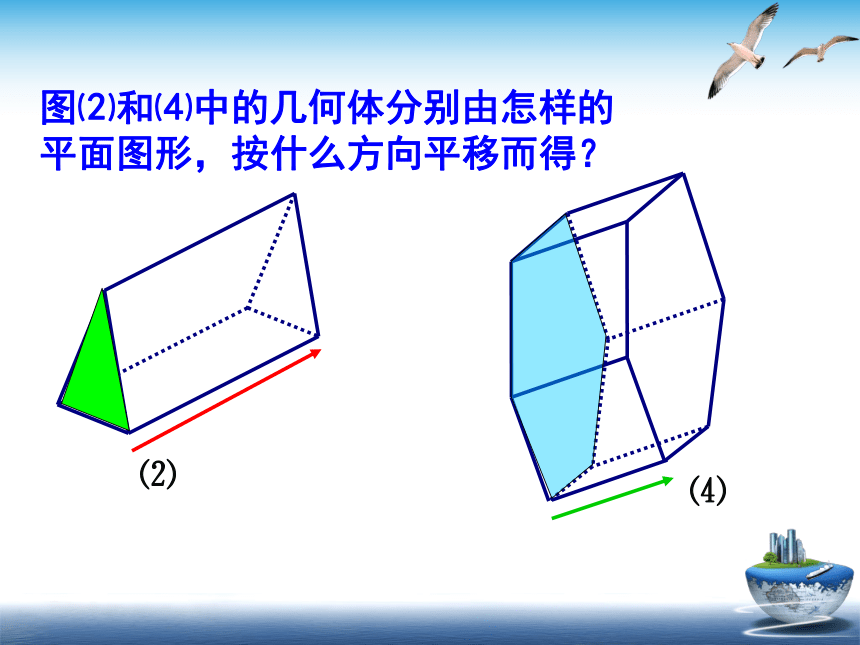
图⑵和⑷中的几何体分别由怎样的
平面图形,按什么方向平移而得?
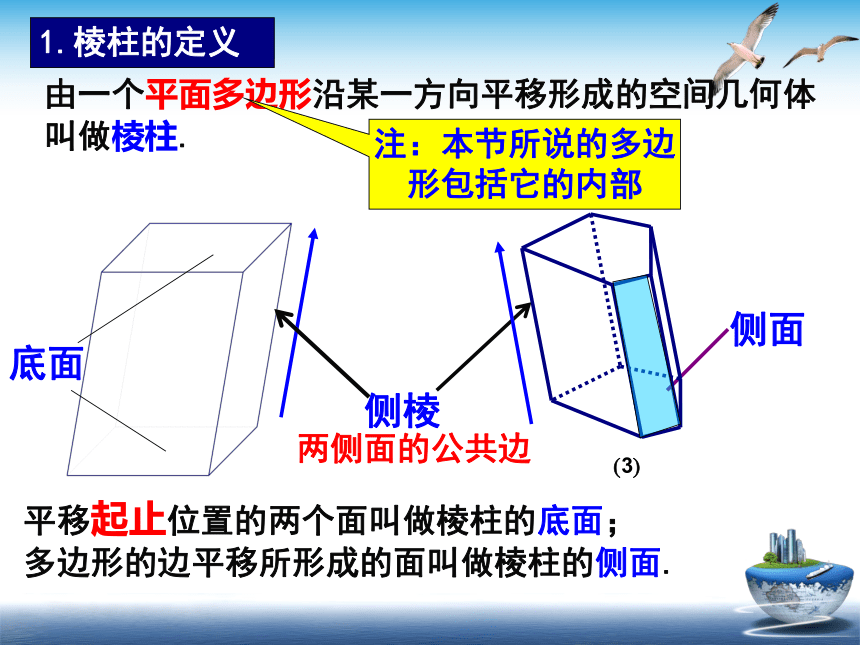
由一个平面多边形沿某一方向平移形成的空间几何体叫做棱柱.
注:本节所说的多边形包括它的内部
底面
侧面
侧棱
平移起止位置的两个面叫做棱柱的底面;
多边形的边平移所形成的面叫做棱柱的侧面.
两侧面的公共边
1.棱柱的定义
3
(
)
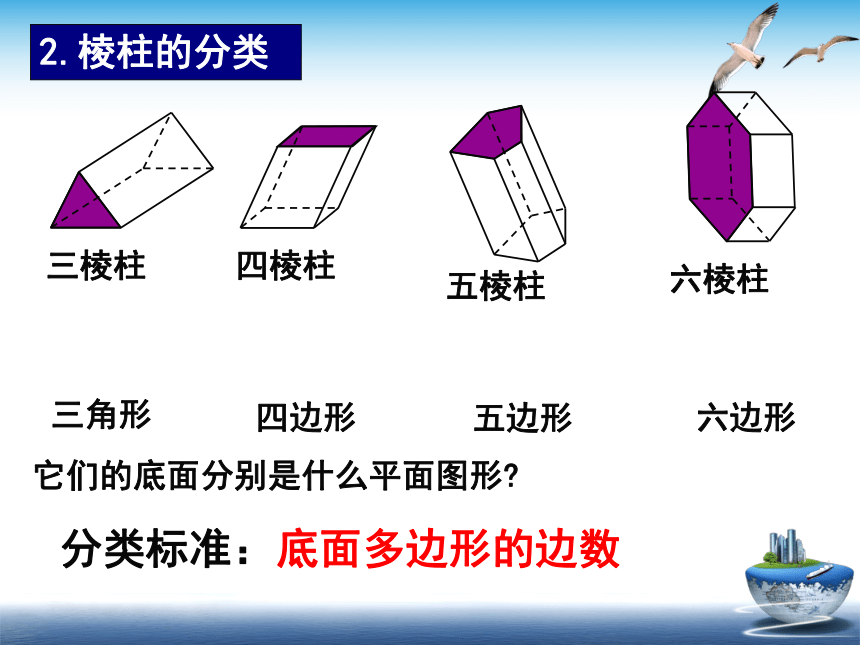
三角形
四边形
五边形
六边形
底面多边形的边数
三棱柱
四棱柱
五棱柱
六棱柱
2.棱柱的分类
分类标准:
它们的底面分别是什么平面图形
棱柱
棱柱
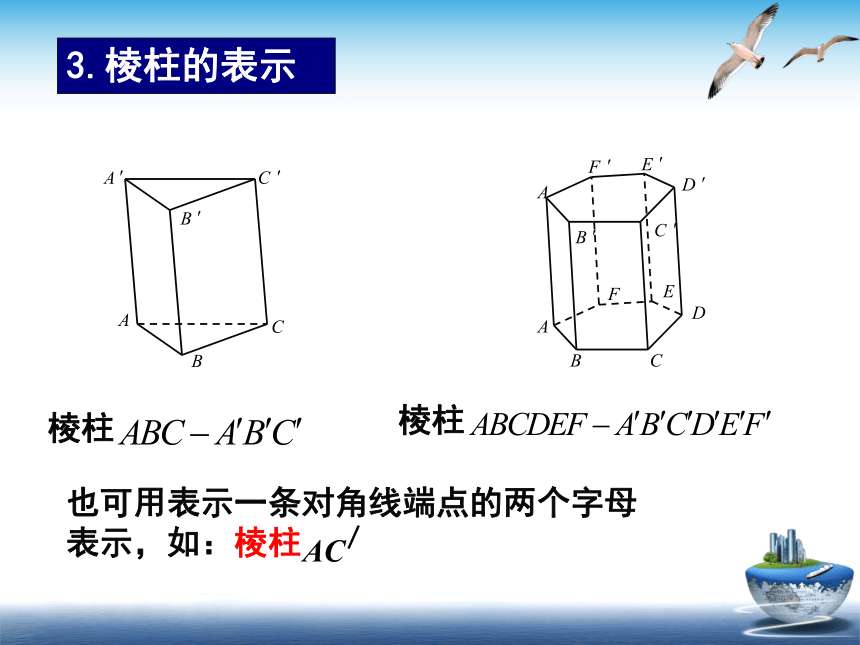
3.棱柱的表示
也可用表示一条对角线端点的两个字母表示,如:棱柱
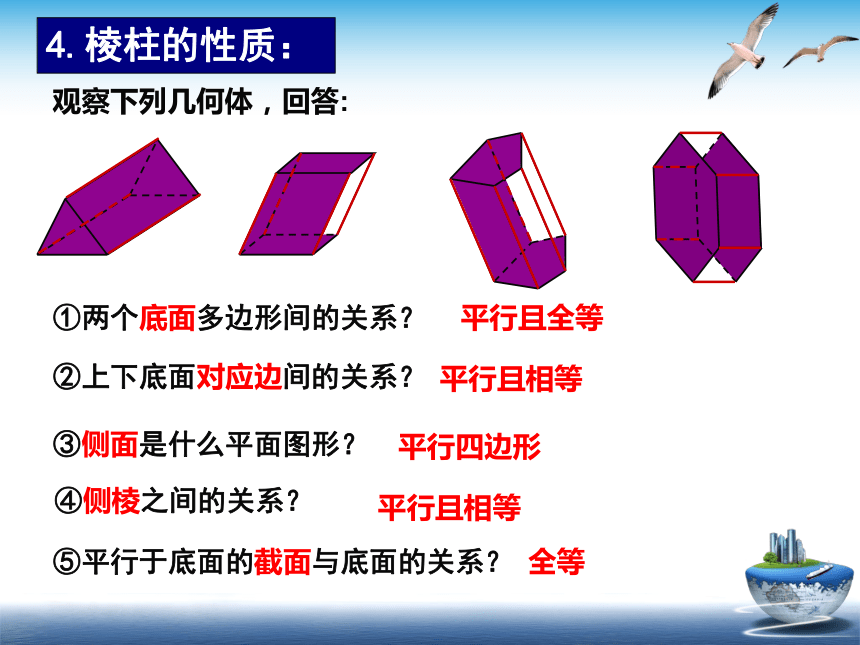
①两个底面多边形间的关系?
②上下底面对应边间的关系?
④侧棱之间的关系?
③侧面是什么平面图形?
平行且全等
平行且相等
平行且相等
平行四边形
⑤平行于底面的截面与底面的关系?
全等
观察下列几何体,回答:
4.棱柱的性质:
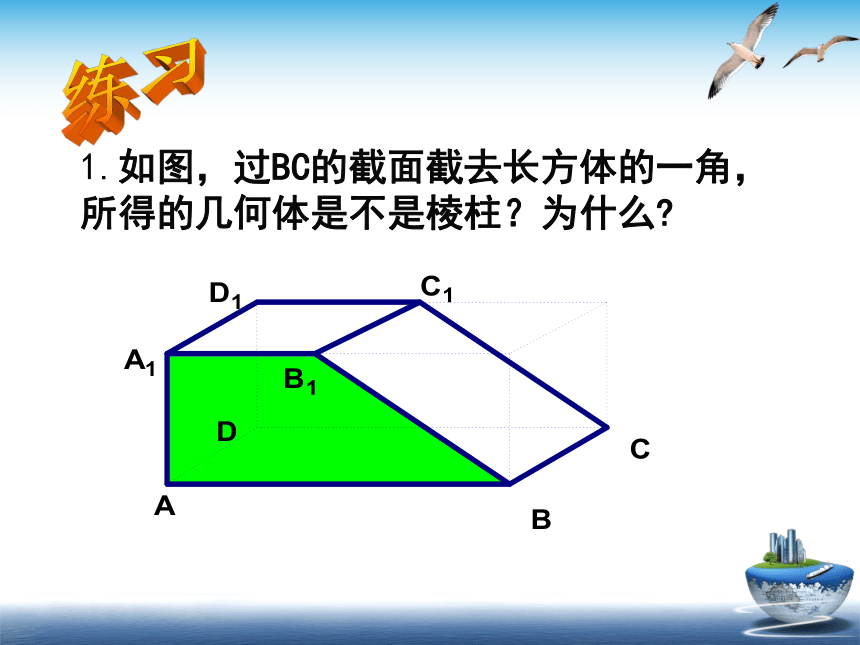
1.如图,过BC的截面截去长方体的一角,所得的几何体是不是棱柱?为什么
2.有两个面互相平行,其余各面都是平行四边形的几何体是棱柱吗?
答:不一定是.
如图所示的几何体,
不是棱柱.
问题2:下面的几何体有什么公共特点?
二.棱锥
1. 棱锥的定义:
当棱柱的一个底面收缩为一个点时,
得到的几何体叫做棱锥.
A
B
C
D
A1
B1
C1
底面
顶点:由棱柱的一个底面收缩而成.
D
C
B
A
S
底面
侧面
D1
侧棱:相邻侧面的公共边.
①底面是多边形(如三角形、四边形、五边形等)
②侧面是
三角形
有一个公共顶点的
2.棱锥的性质:
观察下列棱锥,归纳它们的底面和侧面各有什么特征?
在同一个棱锥中的各个侧面三角形有什么共同特征
3.棱锥的表示与分类
四棱锥S-ABCD
A
S
B
C
D
S
A
B
C
D
E
F
六棱锥S-ABCDEF
底面多边形的边数
分类标准:
思考:有一个面是多边形其余各面是三角形,这个多面体是棱锥吗?
S
A
B
C
D
顶点
侧面
侧棱
底面
D
A
B
C
E
F
F′
A′
E′
D′
B′
C′
侧面
顶点
底面
侧棱
如果用一个平行于棱锥底面的平面去截棱锥,想象一下,那截得的两部分几何体会是什么样的几何体
三.棱台
棱锥
棱台
用一个平行于棱锥底面的平面去截棱锥,得到两个几何体,一个仍然是棱锥,另一个我们称之为棱台.
棱台是棱锥被平行于底面的一个平面所截后,截面和底面之间的部分.
1.棱台的定义
棱锥
上底面
下底面
侧面
侧 棱
2.棱台的元素
3.棱台的分类
三棱台
四棱台
五棱台
六棱台
底面
底面
侧面
侧棱
上底面
下底面
①两个底面多边形间的关系?
②上下底面对应边间的关系?
④侧棱之间的关系?
③侧面是什么平面图形?
平行且相似
平行不等
延长后交于一点
梯形
4.棱台的性质
练习:(1)下列几何体是不是棱台,为什么
(1)
(2)
(2)判断如图所示的几何体是不是棱台,为什么?
优化方案P6页
①和③都不是由棱锥所截得的
②是由棱锥所截得的,但截面不和底面平行
①②③都不是棱台
思考:棱柱、棱锥和棱台都是多面体,当底面发生变化时,它们能否互相转化?
上底扩大
上底缩小
例1.画一个四棱柱和一个三棱台.
多面体 定义 图形及表示 相关概念
棱柱 有两个面互相____,其余各面都是___________,并且每相邻两个四边形的公共边都互相____,由这些面所围成的多面体叫做棱柱
如图可记作: 底面(底):两个互相_____的面
侧面:_________
侧棱:相邻侧面的________
顶点:侧面与底面的__________
平行
平行四边形
平行
平行
其余各面
公共边
公共顶点
多面体 定义 图形及表示 相关概念
棱锥 有一个面是_______,其余各面都是有一个公共顶点的________,由这些面所围成的多面体叫做棱锥 底面(底):________面.
侧面:有公共顶点的各个_______
侧棱:相邻侧面的_______
顶点:各侧面的__________
多边形
三角形
多边形
三角形
公共边
公共顶点
如图可记作:
棱锥S-ABCD
多面体 定义 图形及表示 相关概念
棱台 用一个___________的平面去截棱锥,底面与截面之间的部分叫做棱台
如图可记作:
上底面:原棱锥的_____
下底面:原棱锥的______
侧面:其余各面
侧棱:相邻侧面的公共边
顶点:侧面与上(下)底面的公共顶点
平行于底面
截面
底面
线段
平行四边形
三角形
梯形
平面多边形
棱柱
棱锥
棱台
回顾反思
棱柱、棱锥、棱台之间的关系.
由一个平面多边形沿某一方向平移形成的空间几何体叫做棱柱.
当棱柱的一个底面收缩为一个点时,得到的几何体叫做棱锥.
棱台是棱锥被平行于底面的一个平面所截后,截面和底面之间的部分.
答:长方体有三对平行平面;这三对都可以作为棱柱的底面.
根据下图所给的几何体的
表面展开图,画出立体图形.
例3
解:(1)是以ABCD为底面,
P为顶点的四棱锥.
(2)是以ABCD和A1B1C1D1
为底面的棱柱.
把多面体的表面或侧面沿着某个棱剪开铺在平面上,其图形就是它们的侧面或表面展开图.
优化方案P6页
自我挑战2 某同学制作了一个对面图案均相同的正方体礼品盒,如图所示,则这个正方体礼品盒的表面展开图应该为(对面是相同的图案)( )
A
对于几何体的表面展开,为了解题的方便,常常给多面体的顶点标上字母,先把多面体的底面画出来,然后依次画出各侧面,便可得到其表面展开图。
定义:对于空间上的物体,如果我们只考虑它的的形状和大小,而不考虑其他因素(密度,颜色,位置等),从中抽象出来的空间图形叫做空间几何体.
分类:
1.多面体:由若干个平面多边形围成的几何体;
2.旋转体:由一个平面图形绕它所在平面内的一条直线旋转所形成的封闭几何体.
多面体
旋转体
问题1:仔细观察下面的几何体,它们有什么
共同特点?是怎样形成的?
4
(
)
3
(
)
2
(
)
1
(
)
一.棱柱
图⑴和⑶中的几何体分别由平行四边形和五
边形沿某一方向平移而得.
(1)
(3)
⑵
⑷
图⑵和⑷中的几何体分别由怎样的
平面图形,按什么方向平移而得?
由一个平面多边形沿某一方向平移形成的空间几何体叫做棱柱.
注:本节所说的多边形包括它的内部
底面
侧面
侧棱
平移起止位置的两个面叫做棱柱的底面;
多边形的边平移所形成的面叫做棱柱的侧面.
两侧面的公共边
1.棱柱的定义
3
(
)
三角形
四边形
五边形
六边形
底面多边形的边数
三棱柱
四棱柱
五棱柱
六棱柱
2.棱柱的分类
分类标准:
它们的底面分别是什么平面图形
棱柱
棱柱
3.棱柱的表示
也可用表示一条对角线端点的两个字母表示,如:棱柱
①两个底面多边形间的关系?
②上下底面对应边间的关系?
④侧棱之间的关系?
③侧面是什么平面图形?
平行且全等
平行且相等
平行且相等
平行四边形
⑤平行于底面的截面与底面的关系?
全等
观察下列几何体,回答:
4.棱柱的性质:
1.如图,过BC的截面截去长方体的一角,所得的几何体是不是棱柱?为什么
2.有两个面互相平行,其余各面都是平行四边形的几何体是棱柱吗?
答:不一定是.
如图所示的几何体,
不是棱柱.
问题2:下面的几何体有什么公共特点?
二.棱锥
1. 棱锥的定义:
当棱柱的一个底面收缩为一个点时,
得到的几何体叫做棱锥.
A
B
C
D
A1
B1
C1
底面
顶点:由棱柱的一个底面收缩而成.
D
C
B
A
S
底面
侧面
D1
侧棱:相邻侧面的公共边.
①底面是多边形(如三角形、四边形、五边形等)
②侧面是
三角形
有一个公共顶点的
2.棱锥的性质:
观察下列棱锥,归纳它们的底面和侧面各有什么特征?
在同一个棱锥中的各个侧面三角形有什么共同特征
3.棱锥的表示与分类
四棱锥S-ABCD
A
S
B
C
D
S
A
B
C
D
E
F
六棱锥S-ABCDEF
底面多边形的边数
分类标准:
思考:有一个面是多边形其余各面是三角形,这个多面体是棱锥吗?
S
A
B
C
D
顶点
侧面
侧棱
底面
D
A
B
C
E
F
F′
A′
E′
D′
B′
C′
侧面
顶点
底面
侧棱
如果用一个平行于棱锥底面的平面去截棱锥,想象一下,那截得的两部分几何体会是什么样的几何体
三.棱台
棱锥
棱台
用一个平行于棱锥底面的平面去截棱锥,得到两个几何体,一个仍然是棱锥,另一个我们称之为棱台.
棱台是棱锥被平行于底面的一个平面所截后,截面和底面之间的部分.
1.棱台的定义
棱锥
上底面
下底面
侧面
侧 棱
2.棱台的元素
3.棱台的分类
三棱台
四棱台
五棱台
六棱台
底面
底面
侧面
侧棱
上底面
下底面
①两个底面多边形间的关系?
②上下底面对应边间的关系?
④侧棱之间的关系?
③侧面是什么平面图形?
平行且相似
平行不等
延长后交于一点
梯形
4.棱台的性质
练习:(1)下列几何体是不是棱台,为什么
(1)
(2)
(2)判断如图所示的几何体是不是棱台,为什么?
优化方案P6页
①和③都不是由棱锥所截得的
②是由棱锥所截得的,但截面不和底面平行
①②③都不是棱台
思考:棱柱、棱锥和棱台都是多面体,当底面发生变化时,它们能否互相转化?
上底扩大
上底缩小
例1.画一个四棱柱和一个三棱台.
多面体 定义 图形及表示 相关概念
棱柱 有两个面互相____,其余各面都是___________,并且每相邻两个四边形的公共边都互相____,由这些面所围成的多面体叫做棱柱
如图可记作: 底面(底):两个互相_____的面
侧面:_________
侧棱:相邻侧面的________
顶点:侧面与底面的__________
平行
平行四边形
平行
平行
其余各面
公共边
公共顶点
多面体 定义 图形及表示 相关概念
棱锥 有一个面是_______,其余各面都是有一个公共顶点的________,由这些面所围成的多面体叫做棱锥 底面(底):________面.
侧面:有公共顶点的各个_______
侧棱:相邻侧面的_______
顶点:各侧面的__________
多边形
三角形
多边形
三角形
公共边
公共顶点
如图可记作:
棱锥S-ABCD
多面体 定义 图形及表示 相关概念
棱台 用一个___________的平面去截棱锥,底面与截面之间的部分叫做棱台
如图可记作:
上底面:原棱锥的_____
下底面:原棱锥的______
侧面:其余各面
侧棱:相邻侧面的公共边
顶点:侧面与上(下)底面的公共顶点
平行于底面
截面
底面
线段
平行四边形
三角形
梯形
平面多边形
棱柱
棱锥
棱台
回顾反思
棱柱、棱锥、棱台之间的关系.
由一个平面多边形沿某一方向平移形成的空间几何体叫做棱柱.
当棱柱的一个底面收缩为一个点时,得到的几何体叫做棱锥.
棱台是棱锥被平行于底面的一个平面所截后,截面和底面之间的部分.
答:长方体有三对平行平面;这三对都可以作为棱柱的底面.
根据下图所给的几何体的
表面展开图,画出立体图形.
例3
解:(1)是以ABCD为底面,
P为顶点的四棱锥.
(2)是以ABCD和A1B1C1D1
为底面的棱柱.
把多面体的表面或侧面沿着某个棱剪开铺在平面上,其图形就是它们的侧面或表面展开图.
优化方案P6页
自我挑战2 某同学制作了一个对面图案均相同的正方体礼品盒,如图所示,则这个正方体礼品盒的表面展开图应该为(对面是相同的图案)( )
A
对于几何体的表面展开,为了解题的方便,常常给多面体的顶点标上字母,先把多面体的底面画出来,然后依次画出各侧面,便可得到其表面展开图。
