苏科版数学八年级上册 6.1函数(共38张ppt)
文档属性
| 名称 | 苏科版数学八年级上册 6.1函数(共38张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-08 08:12:33 | ||
图片预览




文档简介
(共38张PPT)
6.1
函数(1)
第六章
一次函数
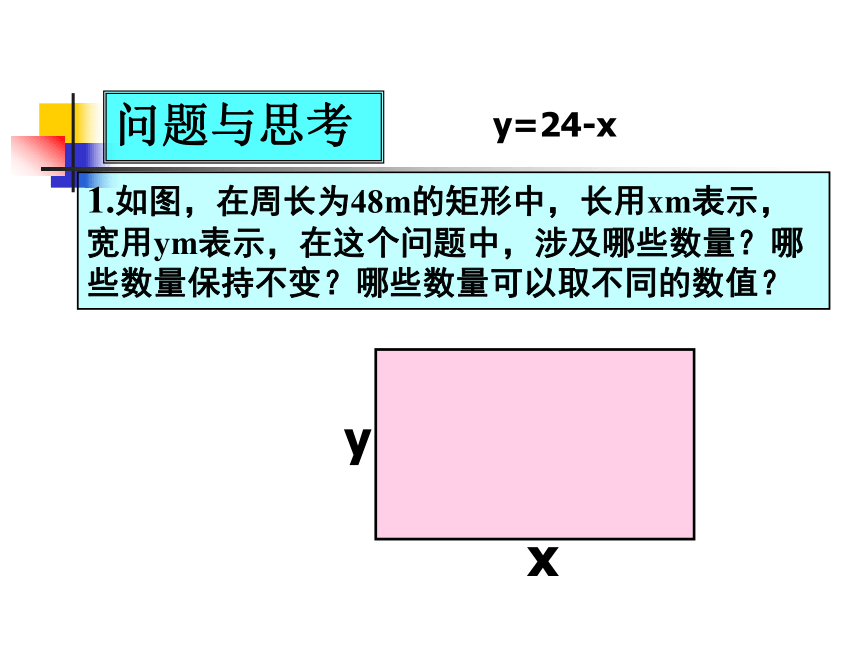
1.如图,在周长为48m的矩形中,长用xm表示,宽用ym表示,在这个问题中,涉及哪些数量?哪些数量保持不变?哪些数量可以取不同的数值?
x
y
问题与思考
y=24-x
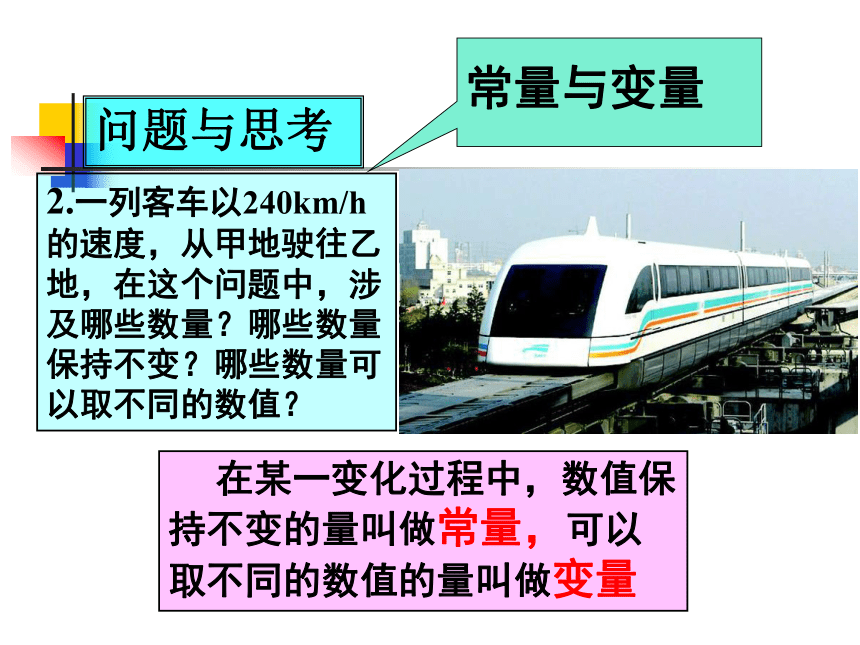
2.一列客车以240km/h的速度,从甲地驶往乙地,在这个问题中,涉及哪些数量?哪些数量保持不变?哪些数量可以取不同的数值?
问题与思考
在某一变化过程中,数值保持不变的量叫做常量,可以取不同的数值的量叫做变量
常量与变量
水位/m
106
120
133
135
…
蓄水/m3
2.30×107
7.09×107
1.18×108
1.23×108
…
你能从他制作的表格中获得哪些信息?
水位高低与水库容量有什么关系?
小明的爸爸是某市水库管理员,他将水库的水位变化与水库蓄水量变化情况列成下表:
从表中可以看到,水库蓄水量随着水位的升高而增大,随着水位的下降而减小,当水位稳定时,蓄水量也稳定不变。
小明的一天
水深(hm
)
106
120
133
135
……
存水量Q(万m3)2.30×107
7.09×107
1.18×108
1.23×108
……
随着
的变化而变化,
当
确定时,
也确定。
存水量Q
水深h
水深h
存水量Q
小明的一天
随着
的
变化而变化,当
确定时,
也确定.
8
14
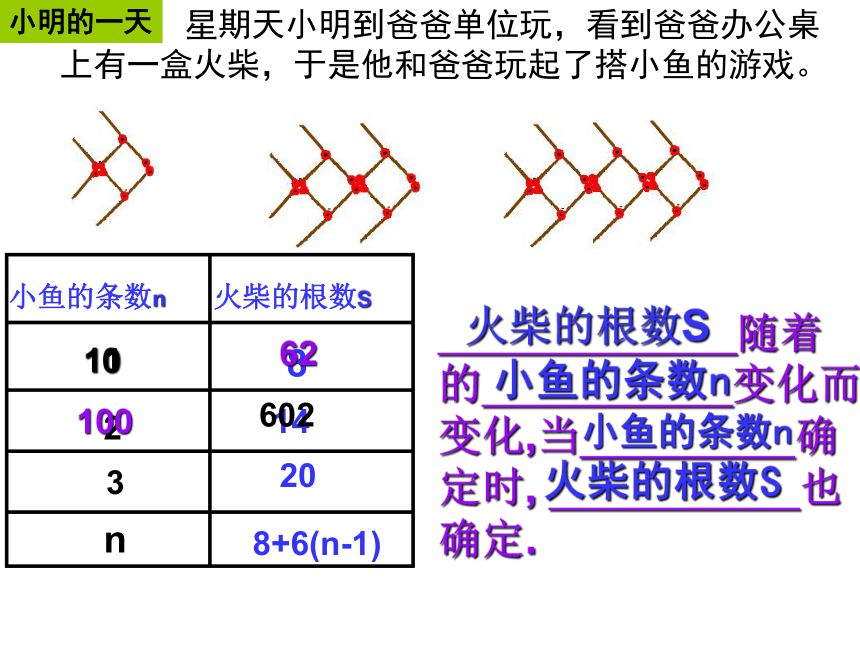
小鱼的条数n
火柴的根数S
1
2
3
8+6(n-1)
n
20
10
62
602
100
火柴的根数S
小鱼的条数n
小鱼的条数n
火柴的根数S
星期天小明到爸爸单位玩,看到爸爸办公桌上有一盒火柴,于是他和爸爸玩起了搭小鱼的游戏。
小明的一天
小明看着窗外宁静的水面,远处的青山,心情特别愉快。于是他走出办公室来的到了水库边,拿起一块小石头扔向水面。水滴激起的波纹可以看作是一个不断向外扩展的圆,变化中圆的面积与半径的大小密切相关,你能大致描述他们之间的关系吗?
小明的一天
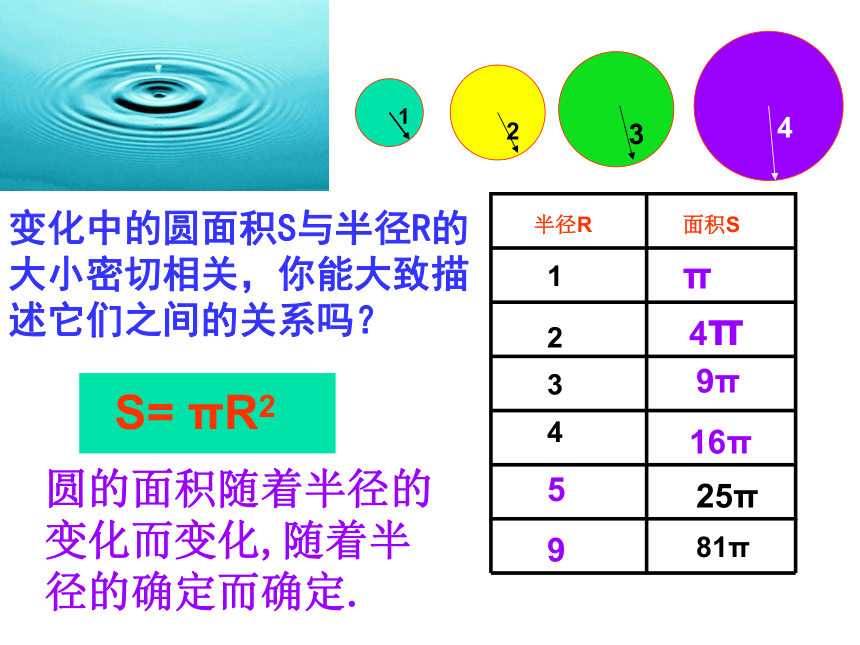
圆的面积随着半径的变化而变化,随着半径的确定而确定.
变化中的圆面积S与半径R的大小密切相关,你能大致描述它们之间的关系吗?
1
2
3
4
1
2
3
4
半径R
面积S
π
4π
9π
16π
25π
81π
5
9
S=
πR2
下午,小明一家三口到游乐场,登上了特别惊险的摩天轮………
小明的一天
O
1
2
3
4
5
6
7
8
9
10
11
12
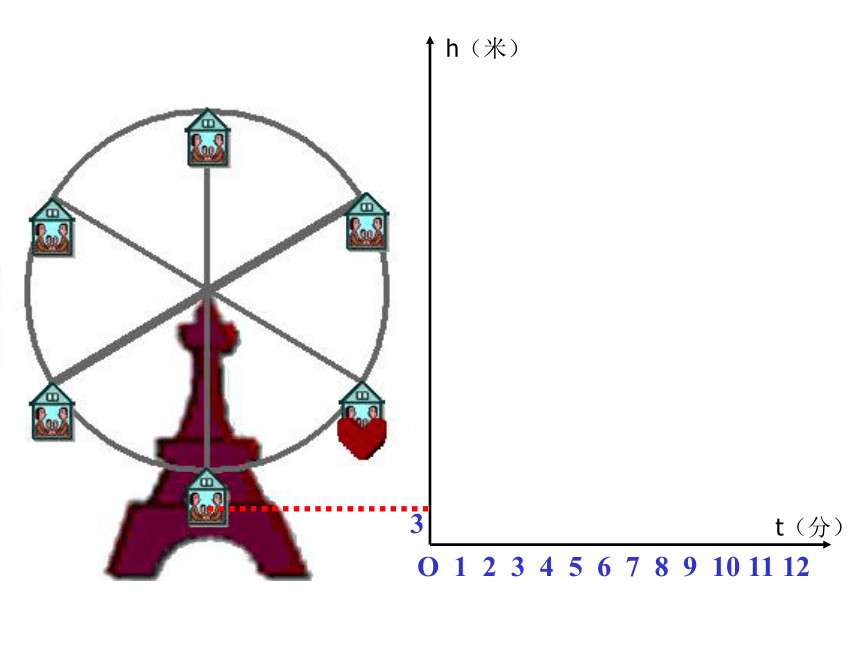
3
h(米)
t(分)
O
1
2
3
4
5
6
7
8
9
10
11
12
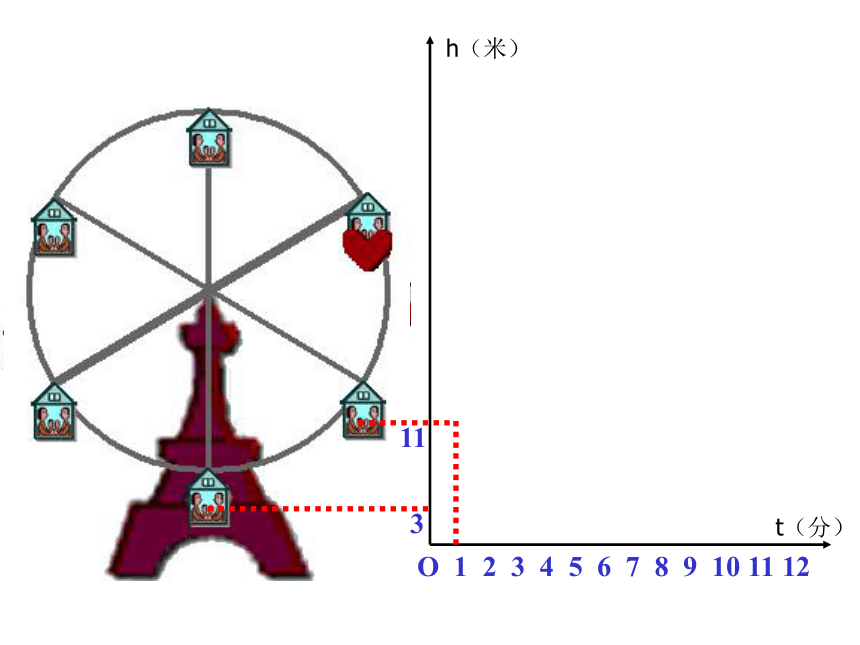
3
11
h(米)
t(分)
O
1
2
3
4
5
6
7
8
9
10
11
12
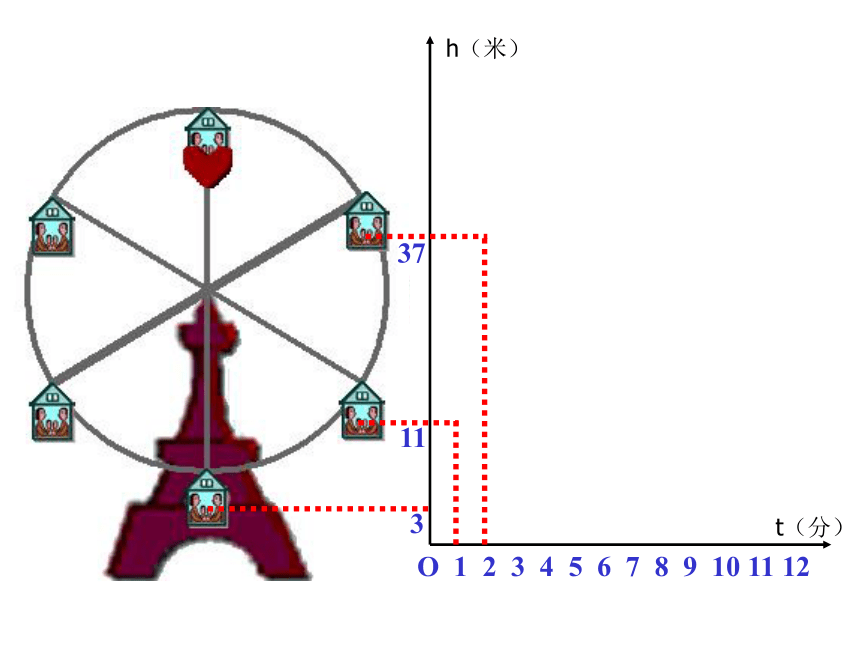
3
11
37
h(米)
t(分)
O
1
2
3
4
5
6
7
8
9
10
11
12
3
11
37
45
h(米)
t(分)
O
1
2
3
4
5
6
7
8
9
10
11
12
3
11
37
45
h(米)
t(分)
O
1
2
3
4
5
6
7
8
9
10
11
12
3
11
37
45
h(米)
t(分)
O
1
2
3
4
5
6
7
8
9
10
11
12
3
11
37
45
h(米)
t(分)
下图反映了旋转时间t(分)与摩天轮上一点的高度h(米)之间的关系。
在一个变化过程中,有两个变量。当其中一个变量变化时,另一个变量也随着发生变化。当一个变量确定时,另一个变量也随着确定。
亲爱的同学你能从小明一天所经历的几个活动中找到它们的共同之处吗?
思考
水位/m
106
120
133
135
…
蓄水/m3
2.30x107
7.09x107
1.18x108
1.23x108
…
S=8+6(n-1)
函数
一般的,如果在一个变化的过程中有两个变量x、y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的函数。其中x是自变量,y是因变量。
也可以说y和x之间存在着函数关系。
圆面积s是半径r的函数吗?
长方形面积S一定,长a是宽b的函数吗?
①一个变化过程,
②两个变量x,y
③对于变量x的每一个值,
变量y都有唯一的值与它对应
我们称y是x的函数,
其中x是自变量,
y是因变量.
函数的概念
思考
水位/m
106
120
133
135
…
蓄水/m3
2.30x107
7.09x107
1.18x108
1.23x108
…
S=8+6(n-1)
高度h是时间t的函数
你能说出变化过程中的函数关系吗?
蓄水量是水位的函数
火柴根数S是小鱼条数n的函数
表示两个变量之间的式子称为函数关系式
例题讲解:
某玩具厂计划生产一种玩具小狗,每日最高产量为40只,且每日产出的产品全部出售,已知生产x只玩具小狗的成本为R元,售价每只为P元,且R、P与x的关系式为R=500+30x,P=170-2x.
(1)上面两个关系式中,分别写出常量和变量.
(2)若获得的利润为y元,指出在求利润的关系中的变量.
1.把一根1米长的铁丝围成一个长方形.
(1)当长方形的宽为0.1m时,长为多少?
(2)当长方形的宽为0.2m时,长为多少?
(3)长方形的长是宽的函数吗?为什么?
课堂练习
2.按图示的运算程序,输入一个实数x,便可输出一个相应的实数y,y是x的函数吗?为什么?
课堂练习
输入x
+2
×5
-4
输出y
①
输入x
开平方
输出y
②
输入x
平方
输出y
③
输入x
5+x
(当x<0时)
5-x
(当x≥0时)
输出y
④
1
2
3
1
0
-1
y
x
图1
y是x的函数吗?
1
2
3
1
0
-1
y
x
图2
y是x的函数吗?
1
2
3
1
0
-1
y
x
图3
y是x的函数吗?
3.指出下面题中的常量、自变量、与函数。并写出它们的函数关系式。
(1)圆周长C与半径R之间的关系;
(2)汽车从40km/h的速度正常行驶,行驶的路程s(km)与t(h)之间的关系。
课堂练习
33
35
37
39
41
43
0
4
8
12
16
20
24
28
32
36
40
44
48
温度/摄氏度
时间/时
4.
如图,骆驼的体温随时间的变化而发生较大的变化。
在这个问题中有变化的数量吗?
哪些是自变量?哪些是因变量?
课堂练习
5.设等腰三角形的周长为60,腰长为x,底为y。
(1)写出y与x之间的函数关系式;
(2)求出当x=20时,y的值,并求出此时三角形的面积。
课堂练习
6.
沙漏是我国计量时间的一种仪器,他根据一个容器里的细沙漏到另一个容器中的数量来计量时间。请说出这个变化过程中的自变量。
课堂练习
7.(1)
圆面积s与直径d之间的关系式为
,其中变量是
,常量是
,自变量为
,因变量为
,
是
的函数.
(2)
一斤苹果1.2元,买x斤这样的苹果y元,其中变量是
,常量是
,自变量为
,因变量为
,
是
的函数.
(3)
写一个日常生活中遇到的函数关系的例子,并指出其中的常量与变量、自变量与因变量.
课堂练习
8.
指出下列变化过程中的常量与变量,自变量与函数:
(1)购买单价是0.4元的铅笔,总金额y(元)
与铅笔数n(个)的关系;
(2)设地面气温是20℃,如果每升高1km,气温下降6℃,气温t(
℃
)与高度h(km)的关系。
课堂练习
9.下列说法正确的个数为:
(1)矩形的宽一定,它的面积是长的函数
(2)人的体重y(公斤)是年龄x(岁)的函数
(3)x+3是自变量x的函数
(4)正方形的边长一定,它的面积是周长的函数
A.
1
B.
2
C.
3
D.
4
课堂练习
10.假设汽车在公路上以每小时80公里的速度匀速行驶,路程s(公里)是时间t(小时)的函数吗?你能写出这个函数关系式吗?在函数关系式中,t可以取不同的值,但可以取任意值吗?
课堂练习
这节课你有哪些收获?
1、四个概念
(1)常量与变量
(2)自变量与函数。
2、两个注意:(1)判断常量与变量
(2)理解函数概念把握三点。
①一个变化过程,
②两个变量,
③对于自变量的每一个值,因变量都有惟一的值与它对应。
数学世家的光荣--函数的出现
17世纪,在瑞士的巴塞尔有一个祖孙五代数学家成员数十人的家族--贝努利家族,其中最著名的是雅各、约翰、丹尼尔。
欧拉从12岁起,就是这个家族成员的好朋友。他和同龄人尼古拉、丹尼尔结识,成为终生盟友,这两位兄长给欧拉讲了许多有趣的数学故事,吸引了他那颗幼小好奇心灵,使欧拉从小立志,将来能像贝努利家族成员一样,腾飞于数学长空,1720年,欧拉在约翰.贝努利教授的推荐下,13岁成为巴塞尔大学的学生.从此他在约翰.贝努利的指导下迅速成长着.欧拉成为了贝努利家庭的一个成员,被世人传为佳话.
函数是中学数学中最重要的概念之一.函数概念产生于300年前.笛卡儿引入了坐标系,使数学发生了巨大变革,但他没用变量这个词.
在数学上使用变量这个词,最早是欧拉的老师约翰.贝努利.他给函数下了这样的定义:“所谓变量的函数,就是变量与常量组成的表达式”
1775年,欧拉在《微分学》中给出了我们教科书中的定义。
读一读
再
见
6.1
函数(1)
第六章
一次函数
1.如图,在周长为48m的矩形中,长用xm表示,宽用ym表示,在这个问题中,涉及哪些数量?哪些数量保持不变?哪些数量可以取不同的数值?
x
y
问题与思考
y=24-x
2.一列客车以240km/h的速度,从甲地驶往乙地,在这个问题中,涉及哪些数量?哪些数量保持不变?哪些数量可以取不同的数值?
问题与思考
在某一变化过程中,数值保持不变的量叫做常量,可以取不同的数值的量叫做变量
常量与变量
水位/m
106
120
133
135
…
蓄水/m3
2.30×107
7.09×107
1.18×108
1.23×108
…
你能从他制作的表格中获得哪些信息?
水位高低与水库容量有什么关系?
小明的爸爸是某市水库管理员,他将水库的水位变化与水库蓄水量变化情况列成下表:
从表中可以看到,水库蓄水量随着水位的升高而增大,随着水位的下降而减小,当水位稳定时,蓄水量也稳定不变。
小明的一天
水深(hm
)
106
120
133
135
……
存水量Q(万m3)2.30×107
7.09×107
1.18×108
1.23×108
……
随着
的变化而变化,
当
确定时,
也确定。
存水量Q
水深h
水深h
存水量Q
小明的一天
随着
的
变化而变化,当
确定时,
也确定.
8
14
小鱼的条数n
火柴的根数S
1
2
3
8+6(n-1)
n
20
10
62
602
100
火柴的根数S
小鱼的条数n
小鱼的条数n
火柴的根数S
星期天小明到爸爸单位玩,看到爸爸办公桌上有一盒火柴,于是他和爸爸玩起了搭小鱼的游戏。
小明的一天
小明看着窗外宁静的水面,远处的青山,心情特别愉快。于是他走出办公室来的到了水库边,拿起一块小石头扔向水面。水滴激起的波纹可以看作是一个不断向外扩展的圆,变化中圆的面积与半径的大小密切相关,你能大致描述他们之间的关系吗?
小明的一天
圆的面积随着半径的变化而变化,随着半径的确定而确定.
变化中的圆面积S与半径R的大小密切相关,你能大致描述它们之间的关系吗?
1
2
3
4
1
2
3
4
半径R
面积S
π
4π
9π
16π
25π
81π
5
9
S=
πR2
下午,小明一家三口到游乐场,登上了特别惊险的摩天轮………
小明的一天
O
1
2
3
4
5
6
7
8
9
10
11
12
3
h(米)
t(分)
O
1
2
3
4
5
6
7
8
9
10
11
12
3
11
h(米)
t(分)
O
1
2
3
4
5
6
7
8
9
10
11
12
3
11
37
h(米)
t(分)
O
1
2
3
4
5
6
7
8
9
10
11
12
3
11
37
45
h(米)
t(分)
O
1
2
3
4
5
6
7
8
9
10
11
12
3
11
37
45
h(米)
t(分)
O
1
2
3
4
5
6
7
8
9
10
11
12
3
11
37
45
h(米)
t(分)
O
1
2
3
4
5
6
7
8
9
10
11
12
3
11
37
45
h(米)
t(分)
下图反映了旋转时间t(分)与摩天轮上一点的高度h(米)之间的关系。
在一个变化过程中,有两个变量。当其中一个变量变化时,另一个变量也随着发生变化。当一个变量确定时,另一个变量也随着确定。
亲爱的同学你能从小明一天所经历的几个活动中找到它们的共同之处吗?
思考
水位/m
106
120
133
135
…
蓄水/m3
2.30x107
7.09x107
1.18x108
1.23x108
…
S=8+6(n-1)
函数
一般的,如果在一个变化的过程中有两个变量x、y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的函数。其中x是自变量,y是因变量。
也可以说y和x之间存在着函数关系。
圆面积s是半径r的函数吗?
长方形面积S一定,长a是宽b的函数吗?
①一个变化过程,
②两个变量x,y
③对于变量x的每一个值,
变量y都有唯一的值与它对应
我们称y是x的函数,
其中x是自变量,
y是因变量.
函数的概念
思考
水位/m
106
120
133
135
…
蓄水/m3
2.30x107
7.09x107
1.18x108
1.23x108
…
S=8+6(n-1)
高度h是时间t的函数
你能说出变化过程中的函数关系吗?
蓄水量是水位的函数
火柴根数S是小鱼条数n的函数
表示两个变量之间的式子称为函数关系式
例题讲解:
某玩具厂计划生产一种玩具小狗,每日最高产量为40只,且每日产出的产品全部出售,已知生产x只玩具小狗的成本为R元,售价每只为P元,且R、P与x的关系式为R=500+30x,P=170-2x.
(1)上面两个关系式中,分别写出常量和变量.
(2)若获得的利润为y元,指出在求利润的关系中的变量.
1.把一根1米长的铁丝围成一个长方形.
(1)当长方形的宽为0.1m时,长为多少?
(2)当长方形的宽为0.2m时,长为多少?
(3)长方形的长是宽的函数吗?为什么?
课堂练习
2.按图示的运算程序,输入一个实数x,便可输出一个相应的实数y,y是x的函数吗?为什么?
课堂练习
输入x
+2
×5
-4
输出y
①
输入x
开平方
输出y
②
输入x
平方
输出y
③
输入x
5+x
(当x<0时)
5-x
(当x≥0时)
输出y
④
1
2
3
1
0
-1
y
x
图1
y是x的函数吗?
1
2
3
1
0
-1
y
x
图2
y是x的函数吗?
1
2
3
1
0
-1
y
x
图3
y是x的函数吗?
3.指出下面题中的常量、自变量、与函数。并写出它们的函数关系式。
(1)圆周长C与半径R之间的关系;
(2)汽车从40km/h的速度正常行驶,行驶的路程s(km)与t(h)之间的关系。
课堂练习
33
35
37
39
41
43
0
4
8
12
16
20
24
28
32
36
40
44
48
温度/摄氏度
时间/时
4.
如图,骆驼的体温随时间的变化而发生较大的变化。
在这个问题中有变化的数量吗?
哪些是自变量?哪些是因变量?
课堂练习
5.设等腰三角形的周长为60,腰长为x,底为y。
(1)写出y与x之间的函数关系式;
(2)求出当x=20时,y的值,并求出此时三角形的面积。
课堂练习
6.
沙漏是我国计量时间的一种仪器,他根据一个容器里的细沙漏到另一个容器中的数量来计量时间。请说出这个变化过程中的自变量。
课堂练习
7.(1)
圆面积s与直径d之间的关系式为
,其中变量是
,常量是
,自变量为
,因变量为
,
是
的函数.
(2)
一斤苹果1.2元,买x斤这样的苹果y元,其中变量是
,常量是
,自变量为
,因变量为
,
是
的函数.
(3)
写一个日常生活中遇到的函数关系的例子,并指出其中的常量与变量、自变量与因变量.
课堂练习
8.
指出下列变化过程中的常量与变量,自变量与函数:
(1)购买单价是0.4元的铅笔,总金额y(元)
与铅笔数n(个)的关系;
(2)设地面气温是20℃,如果每升高1km,气温下降6℃,气温t(
℃
)与高度h(km)的关系。
课堂练习
9.下列说法正确的个数为:
(1)矩形的宽一定,它的面积是长的函数
(2)人的体重y(公斤)是年龄x(岁)的函数
(3)x+3是自变量x的函数
(4)正方形的边长一定,它的面积是周长的函数
A.
1
B.
2
C.
3
D.
4
课堂练习
10.假设汽车在公路上以每小时80公里的速度匀速行驶,路程s(公里)是时间t(小时)的函数吗?你能写出这个函数关系式吗?在函数关系式中,t可以取不同的值,但可以取任意值吗?
课堂练习
这节课你有哪些收获?
1、四个概念
(1)常量与变量
(2)自变量与函数。
2、两个注意:(1)判断常量与变量
(2)理解函数概念把握三点。
①一个变化过程,
②两个变量,
③对于自变量的每一个值,因变量都有惟一的值与它对应。
数学世家的光荣--函数的出现
17世纪,在瑞士的巴塞尔有一个祖孙五代数学家成员数十人的家族--贝努利家族,其中最著名的是雅各、约翰、丹尼尔。
欧拉从12岁起,就是这个家族成员的好朋友。他和同龄人尼古拉、丹尼尔结识,成为终生盟友,这两位兄长给欧拉讲了许多有趣的数学故事,吸引了他那颗幼小好奇心灵,使欧拉从小立志,将来能像贝努利家族成员一样,腾飞于数学长空,1720年,欧拉在约翰.贝努利教授的推荐下,13岁成为巴塞尔大学的学生.从此他在约翰.贝努利的指导下迅速成长着.欧拉成为了贝努利家庭的一个成员,被世人传为佳话.
函数是中学数学中最重要的概念之一.函数概念产生于300年前.笛卡儿引入了坐标系,使数学发生了巨大变革,但他没用变量这个词.
在数学上使用变量这个词,最早是欧拉的老师约翰.贝努利.他给函数下了这样的定义:“所谓变量的函数,就是变量与常量组成的表达式”
1775年,欧拉在《微分学》中给出了我们教科书中的定义。
读一读
再
见
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
