正方形
图片预览







文档简介
(共25张PPT)
教学目标:
1.掌握正方形的定义,理解正方形与平行四边形、菱形、矩形的关系.
2.掌握正方形的性质定理1和性质定理2.
3.掌握正方形的判定方法.
4.正确运用正方形的性质和判定解题.
教学重点:
1、正方形的性质定理1和性质定理2.
2.正方形的判定方法.
教学难点:
运用正方形的性质和判定解题.
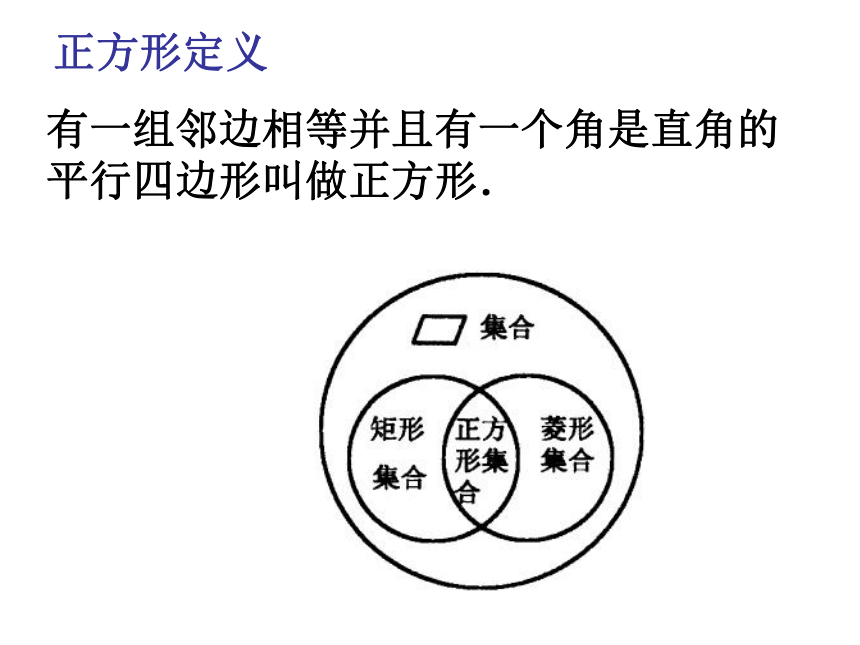
正方形定义
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
正方形性质定理1
正方形的四个角都是直角,四条边相等.
正方形性质定理2
正方形的两条对角钱相等并且互相垂直平分,每一条对角线平分一组对角.
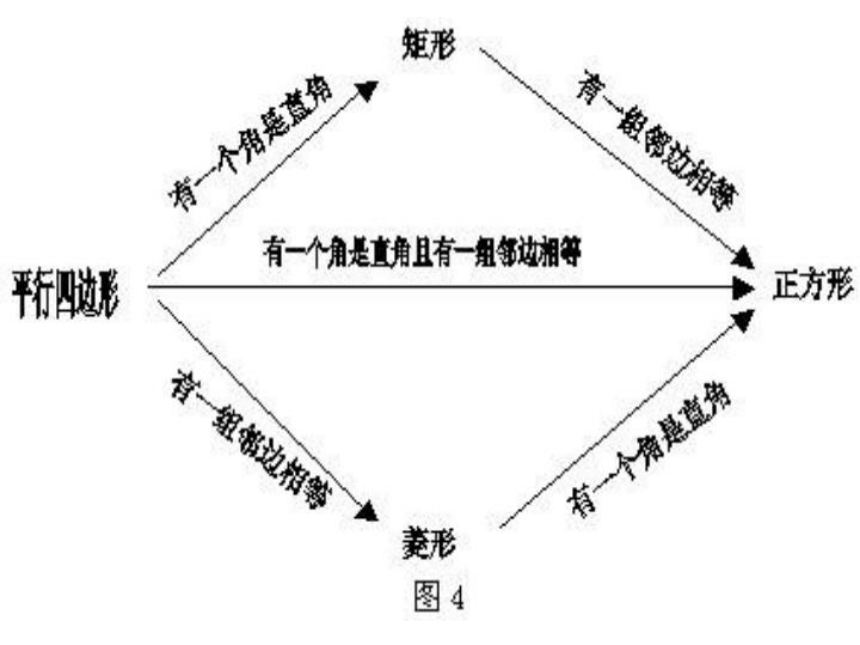
正方形的判定方法
(1)矩形、菱形法:先判定四边形是矩形,再判定这个矩形是菱形(一组邻边相等的矩形);或者先判定四边形是菱形,再判定这个菱形也是矩形(有一个角是直角的菱形).
(2)定义法:有一组邻边相等且有一个角是直角的平行四边行是正方形,这是直接利用定义来判定的.
①对角线相等的菱形是正方形吗?为什么?
②对角线互相垂直的矩形是正方形吗?为什么?
③对角线垂直且相等的四边形是正方形吗?为什么?
④四条边都相等的四边形是正方形吗?为什么?
判断下列命题是否是真命题?
1. 正方形的两条对角线互相垂直平分。
2. 每一个矩形都是正方形。
3. 每一个正方形都是菱形。
4. 一条对角线把一个正方形分成两个等腰直角三角形。
(1)延长正方形 ABCD 的边DC 到 E ,使CE=CA ,连结AE 交 BC 于点F ,则∠FAC= 。 .
(2)正方形 ABCD 的边长为4, E 为 AB 上的一点,BE=3AE ,F为BC的中点,则S△DEF:S正方形ABCD= 。
已知正方形ABCD,延长AB到E,连结EC,作AG⊥EC于G,AG交BC于F,
求证:AF=CE。
在已知锐角三角形ABC外边作正方形ABDE和正方形ACFG,
求证:BG=CE。
O为正方形ABCD对角线AC、BD的交点,AEFC为菱形,EH⊥AC于H。
求证:EH= FC。
1
2
H
F
E
O
D
C
B
A
已知:F为正方形ABCD的边BC上的一点,AF平分∠EAD交CD于点F.
求证:AE=BE+DF。
在正方形ABCD中,E、F分别是BC、AB的中点,DE、CF相交于M,
求证:AD=AM。
有以正方形一边中点为端点的线段时,常把这条线段延长,构造全等三角形。
A
F
B
C
D
M
E
分析:欲证AD=AM,只需证明∠1=∠2,但要根据题目条件直接证明∠1=∠2比较困难,考虑到E、F是正方形的两边中点,容易证明得:△BCF≌△CDF,得∠3=∠4,而∠4+∠BCF=90°.由此DE⊥CF,这是要证AD=AM,是否想到与直角有关的等腰三角形?只需延长CF、DA交于N,即可出现直角三角形MND,只要证明A是ND中点即可。这是是否发现△BCF≌△ANF?由AN=BC=AD,从而A是ND中点,MA是直角三角形MND的斜边ND上的中线。问题得证。
正方形ABCD 的边长为a ,正方形 DEFG 的边长为 b , P 为AD 的中点,PG=PC ,延长FE 交AB 于点 H .
求证: .
正方形 ABCD 与正方形 CEFG 中, D 、C、G 三点共线,连结 DE 、BG ,且延长 DE 交 BG 于H .
求证:DH⊥BG。
正方形 ABCD 中,AC 、BD 交于 O 点,点 M 是 AC 上任意一点,ME⊥AB ,MF⊥BC ,垂足为E、F .
求证:△ OEF 是等腰直角三角形.
在正方形 ABCD 中, M 是CD 的中点, E 是CD 上一点,且 ∠BAE=2∠DAM .
求证:AE=BC+CE。
设A、B为直线m上两点,C为m外一点,分别以AC、BC为边作正方形CADE和CBFG。
求证 :点D、F到m的距离之和为定值。
m
C
B
G
F
F‘
E
D
A
D’
C‘
已知:过正方形ABCD对角线BD上一点P,作PE⊥BC于E,PF⊥CD于F,
求证:AP=EF。
F
E
P
D
C
B
A
N
AP⊥EF吗?
课后反馈: 学生对正方形的定义、正方形与平行四边形、菱形、矩形的关系、
正方形的性质定理掌握的较好。对正方形的判定方法,综合运用正方形的性质和判定解题的能力需要提高。
教学目标:
1.掌握正方形的定义,理解正方形与平行四边形、菱形、矩形的关系.
2.掌握正方形的性质定理1和性质定理2.
3.掌握正方形的判定方法.
4.正确运用正方形的性质和判定解题.
教学重点:
1、正方形的性质定理1和性质定理2.
2.正方形的判定方法.
教学难点:
运用正方形的性质和判定解题.
正方形定义
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
正方形性质定理1
正方形的四个角都是直角,四条边相等.
正方形性质定理2
正方形的两条对角钱相等并且互相垂直平分,每一条对角线平分一组对角.
正方形的判定方法
(1)矩形、菱形法:先判定四边形是矩形,再判定这个矩形是菱形(一组邻边相等的矩形);或者先判定四边形是菱形,再判定这个菱形也是矩形(有一个角是直角的菱形).
(2)定义法:有一组邻边相等且有一个角是直角的平行四边行是正方形,这是直接利用定义来判定的.
①对角线相等的菱形是正方形吗?为什么?
②对角线互相垂直的矩形是正方形吗?为什么?
③对角线垂直且相等的四边形是正方形吗?为什么?
④四条边都相等的四边形是正方形吗?为什么?
判断下列命题是否是真命题?
1. 正方形的两条对角线互相垂直平分。
2. 每一个矩形都是正方形。
3. 每一个正方形都是菱形。
4. 一条对角线把一个正方形分成两个等腰直角三角形。
(1)延长正方形 ABCD 的边DC 到 E ,使CE=CA ,连结AE 交 BC 于点F ,则∠FAC= 。 .
(2)正方形 ABCD 的边长为4, E 为 AB 上的一点,BE=3AE ,F为BC的中点,则S△DEF:S正方形ABCD= 。
已知正方形ABCD,延长AB到E,连结EC,作AG⊥EC于G,AG交BC于F,
求证:AF=CE。
在已知锐角三角形ABC外边作正方形ABDE和正方形ACFG,
求证:BG=CE。
O为正方形ABCD对角线AC、BD的交点,AEFC为菱形,EH⊥AC于H。
求证:EH= FC。
1
2
H
F
E
O
D
C
B
A
已知:F为正方形ABCD的边BC上的一点,AF平分∠EAD交CD于点F.
求证:AE=BE+DF。
在正方形ABCD中,E、F分别是BC、AB的中点,DE、CF相交于M,
求证:AD=AM。
有以正方形一边中点为端点的线段时,常把这条线段延长,构造全等三角形。
A
F
B
C
D
M
E
分析:欲证AD=AM,只需证明∠1=∠2,但要根据题目条件直接证明∠1=∠2比较困难,考虑到E、F是正方形的两边中点,容易证明得:△BCF≌△CDF,得∠3=∠4,而∠4+∠BCF=90°.由此DE⊥CF,这是要证AD=AM,是否想到与直角有关的等腰三角形?只需延长CF、DA交于N,即可出现直角三角形MND,只要证明A是ND中点即可。这是是否发现△BCF≌△ANF?由AN=BC=AD,从而A是ND中点,MA是直角三角形MND的斜边ND上的中线。问题得证。
正方形ABCD 的边长为a ,正方形 DEFG 的边长为 b , P 为AD 的中点,PG=PC ,延长FE 交AB 于点 H .
求证: .
正方形 ABCD 与正方形 CEFG 中, D 、C、G 三点共线,连结 DE 、BG ,且延长 DE 交 BG 于H .
求证:DH⊥BG。
正方形 ABCD 中,AC 、BD 交于 O 点,点 M 是 AC 上任意一点,ME⊥AB ,MF⊥BC ,垂足为E、F .
求证:△ OEF 是等腰直角三角形.
在正方形 ABCD 中, M 是CD 的中点, E 是CD 上一点,且 ∠BAE=2∠DAM .
求证:AE=BC+CE。
设A、B为直线m上两点,C为m外一点,分别以AC、BC为边作正方形CADE和CBFG。
求证 :点D、F到m的距离之和为定值。
m
C
B
G
F
F‘
E
D
A
D’
C‘
已知:过正方形ABCD对角线BD上一点P,作PE⊥BC于E,PF⊥CD于F,
求证:AP=EF。
F
E
P
D
C
B
A
N
AP⊥EF吗?
课后反馈: 学生对正方形的定义、正方形与平行四边形、菱形、矩形的关系、
正方形的性质定理掌握的较好。对正方形的判定方法,综合运用正方形的性质和判定解题的能力需要提高。
