指数函数的概念与性质

(共18张PPT)
2.1.2 指数函数及其性质
必修一 新课标人教A版
导入新课
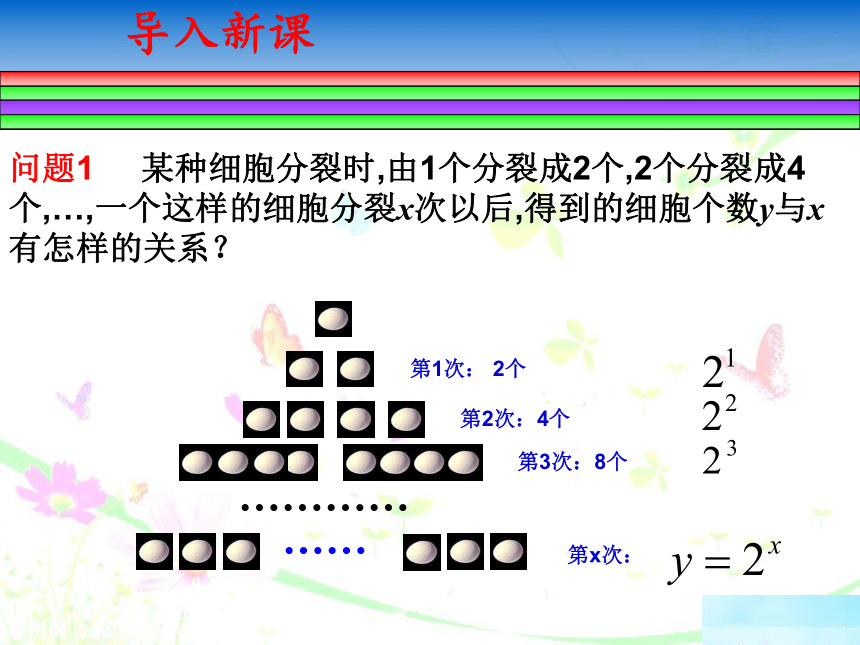
问题1 某种细胞分裂时,由1个分裂成2个,2个分裂成4个,…,一个这样的细胞分裂x次以后,得到的细胞个数y与x有怎样的关系？
…………
……
第1次： 2个
第2次：4个
第3次：8个
第x次：
导入新课
问题2 一种放射性物质不断衰减为其它物质，每经过一年剩留量约为原来的84%，则这种物质经过x年后的剩留量是多少？
分析：
设该物质经过x年后的剩留量为y
若设该物质原有量为1
则经过一年剩留量为:
经过二年剩留量为:
经过三年剩留量为:
……
即经过x年后的剩留量是
问题探究
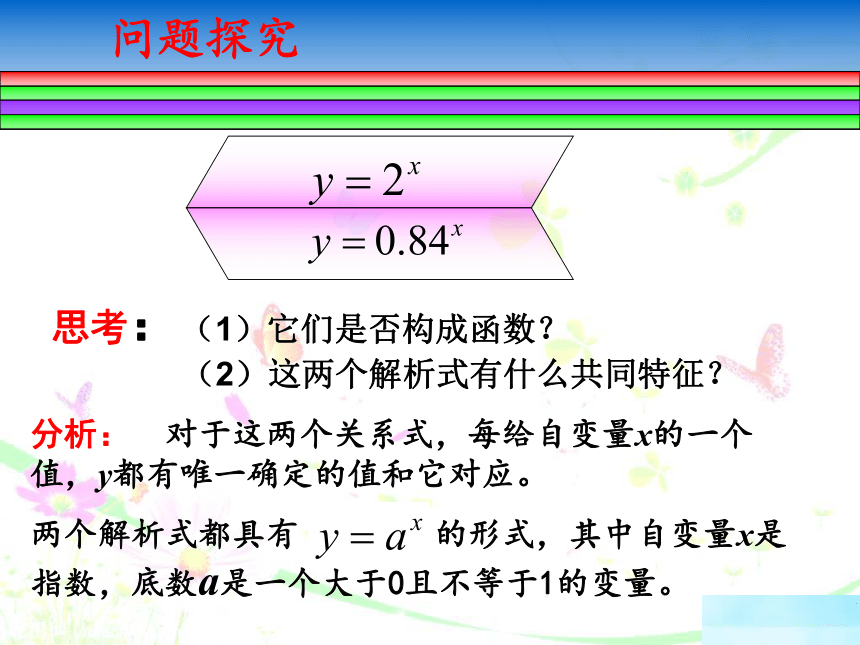
思考：（1）它们是否构成函数？
（2）这两个解析式有什么共同特征？
分析： 对于这两个关系式，每给自变量x的一个 值，y都有唯一确定的值和它对应。
两个解析式都具有 的形式，其中自变量x是指数，底数a是一个大于0且不等于1的变量。
一、指数函数的概念
注意 ：
（1）ax为一个整体，前面系数为1；
（2）a>0,且 a≠1 ;
（3）自变量x在幂指数的位置且为单个x；
思考:为什么概念中明确规定a>0,且a≠1

为什么概念中明确规定a>0,且 a≠1
(3) 若a=1时，函数值y=1，没有研究的必要.
练习
判断下列哪些函数是指数函数.
×
×
×
√
√
√
二、指数函数的图像和性质
画函数图象的步骤：
列表
描点
连线
1、在方格纸上画出： 的图像，并分析函数图象有哪些特点？
列表：
x -2 -1 0 1 2
1
1
1
2
4
4
2
3
1
9
3
9
0
1
1
关于y轴对称
描点、连线
a越大，曲线约往y轴靠近，且都过定点（0,1）
0
1
1
0
1
1
0
1
0
1
y=ax (0y=ax (a>1)
指数函数性质一览表
函数
y=ax (a>1)
y=ax (0图
象
定义域
R
值 域
性质
（0，1 ）
单调性
在R上是增函数
在R上是减函数
若x>0, 则y>1
若x<0, 则0若x<0, 则y>1
若x>0, 则0定 点
没有奇偶性
没有最值
归纳
左右无限上冲天，
永与横轴不沾边.
大 1 增，小 1 减，
图象恒过(0,1)点.
口诀
学以致用
例1、比较下列各组数的大小：
① ②
③ ④
解：①
1.72.5、1.73可以看作函数y=1.7x的两个函数值
∵1.7>1
∴ y=1.7x在R上是增函数
又∵2.5<3
∴ 1.72.5 < 1.73
在a1=0.8，a2=0.6下的函数值
解：② 可以看做是函数
∵ a1<0 , a2<0
∴函数 为减函数
又∵ , x=1.3>0
∴0.81.3>0.61.3
解：③
∵1.70.3>1，而0.93.1<1
解：④
②异底同指:构造函数法(多个),利用函数图象在y轴左右两侧的特点。
比较指数幂大小的方法：
①同底异指：构造函数法(一个), 利用函数的单调性,若底数是参变量要注意分类讨论。
③异底异指:寻求中间量
课堂小结
1.指数函数的概念
2.指数函数的图像和性质
3.指数函数性质的简单应用
数形结合，由具体到一般
1.定义域为R，值域为(0,+ ).
2.当x=0时，y=1
3.在R上是增函数
3.在R上是减函数
4.非奇非偶函数
x
函 数 图 象
1.定义域为R，值域为(0,+ ).
2.当x=0时，y=1
3.在R上是增函数
4.非奇非偶函数
1.定义域为R，值域为(0,+ ).
2.当x=0时，y=1
3.在R上是增函数
4.非奇非偶函数
y
0
a>1
函数性质
思想与方法:
y=1
(0,1)
x
在第一象限内，按逆时针方向旋转，底数a越来越大
0课后作业
练习：P58: 1 , 2
作业: P59: 5 , 7