初数七下 知识点精讲 立方根 课件(共9张PPT)
文档属性
| 名称 | 初数七下 知识点精讲 立方根 课件(共9张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-13 14:48:55 | ||
图片预览



文档简介
立方根
考点聚焦
1.题型:填空题、选择题和计算题;
2.内容:主要考查立方根的定义和性质以及立方根的求法;
3.难度:中考主要以填空题、选择题的形式出现,难度不大。
知识梳理
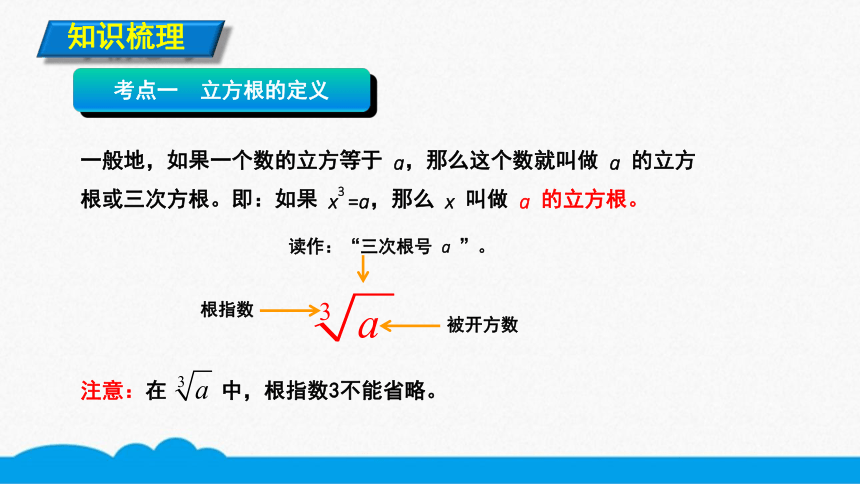
考点一 立方根的定义
一般地,如果一个数的立方等于 a,那么这个数就叫做 a 的立方根或三次方根。即:如果 x3 =a,那么 x 叫做 a 的立方根。
注意:在 中,根指数3不能省略。
被开方数
读作:“三次根号 a ”。
根指数
知识梳理
考点二 立方根的性质
立方根的性质:
注意:任何数的立方根有且只有一个。
1、正数有一个正的立方根。如:27的立方根: 。
2、负数有一个负的立方根。如:-27的立方根: 。
3、零的立方根是零。如:0的立方根: 。
4、互为相反数的两数的立方根也互为相反数。
求各数的立方根要注意:任何数都有立方根且只有一个,求立方根时被开方数是正数开方得的数就是正数,被开方数是负数开方得的数就是负数,0的立方根是零。
方法点拨
典例剖析
求下列各式的值:
(1)
(2)
(3)
(-5)3=-125
0.13=0.001
53=125
=-5
=5
=-0.1
典例剖析
下列各项中正确的是( )。
A. 的立方根是 。
B.算术平方根和立方根都等于本身的数只有0。
C.-8的立方根是-2,但-8没有平方根。
D.4的平方根是±2,但4没有立方根。
C
立方根只有一个。
还有1。
4的立方根是 。
正数有一正一负两个平方根,而正数只有一个正的立方根。负数没有平方根,而负数有一个负的立方根。立方根是它本身的数有1、0、-1,平方根是它本身的数只有0,算术平方根是它本身的数有1、0。
方法点拨
备考技法
1、立方和开立方互为逆运算。
2、0的平方根和立方根都是0。
3、平方根的根指数“2”可以省略,但立方根中的根指数“3”不能省略,
要写在根号的左上角。
4、开平方时被开方数要大于或等于0,而开立方时被开方数可以是任何实
数。
5、被开方数的小数点每向左(右)移动三位,则其立方根的值向左(右)
移动一位。
立方根
性质
定义:一个数的立方等于 a,那么这个数就叫做 a 的立方根或三次方根。
思维导图
正数的立方根是正数;
负数的立方根是负数;
0的立方根是0。
表示:
元申小课 必有收获
考点聚焦
1.题型:填空题、选择题和计算题;
2.内容:主要考查立方根的定义和性质以及立方根的求法;
3.难度:中考主要以填空题、选择题的形式出现,难度不大。
知识梳理
考点一 立方根的定义
一般地,如果一个数的立方等于 a,那么这个数就叫做 a 的立方根或三次方根。即:如果 x3 =a,那么 x 叫做 a 的立方根。
注意:在 中,根指数3不能省略。
被开方数
读作:“三次根号 a ”。
根指数
知识梳理
考点二 立方根的性质
立方根的性质:
注意:任何数的立方根有且只有一个。
1、正数有一个正的立方根。如:27的立方根: 。
2、负数有一个负的立方根。如:-27的立方根: 。
3、零的立方根是零。如:0的立方根: 。
4、互为相反数的两数的立方根也互为相反数。
求各数的立方根要注意:任何数都有立方根且只有一个,求立方根时被开方数是正数开方得的数就是正数,被开方数是负数开方得的数就是负数,0的立方根是零。
方法点拨
典例剖析
求下列各式的值:
(1)
(2)
(3)
(-5)3=-125
0.13=0.001
53=125
=-5
=5
=-0.1
典例剖析
下列各项中正确的是( )。
A. 的立方根是 。
B.算术平方根和立方根都等于本身的数只有0。
C.-8的立方根是-2,但-8没有平方根。
D.4的平方根是±2,但4没有立方根。
C
立方根只有一个。
还有1。
4的立方根是 。
正数有一正一负两个平方根,而正数只有一个正的立方根。负数没有平方根,而负数有一个负的立方根。立方根是它本身的数有1、0、-1,平方根是它本身的数只有0,算术平方根是它本身的数有1、0。
方法点拨
备考技法
1、立方和开立方互为逆运算。
2、0的平方根和立方根都是0。
3、平方根的根指数“2”可以省略,但立方根中的根指数“3”不能省略,
要写在根号的左上角。
4、开平方时被开方数要大于或等于0,而开立方时被开方数可以是任何实
数。
5、被开方数的小数点每向左(右)移动三位,则其立方根的值向左(右)
移动一位。
立方根
性质
定义:一个数的立方等于 a,那么这个数就叫做 a 的立方根或三次方根。
思维导图
正数的立方根是正数;
负数的立方根是负数;
0的立方根是0。
表示:
元申小课 必有收获
