初数八上 知识点精讲 因式分解——十字相乘法 课件(共8张PPT)
文档属性
| 名称 | 初数八上 知识点精讲 因式分解——十字相乘法 课件(共8张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-13 00:00:00 | ||
图片预览



文档简介
因式分解——
十字相乘法
考点聚焦
1. 要求:掌握十字相乘的方法,灵活进行因式分解;
2. 形式:考题多填空形式出现;
3. 联系:整式乘法,分式化简,代数式恒等变形。
考点一 十字相乘法
知识梳理
定义:
利用十字交叉线来分解系数,把二次三项式分解因式的方法叫做十字相乘法。
步骤:
1、竖分二次项与常数项;
2、交叉相乘,和相加;
3、检验确定,横写因式。
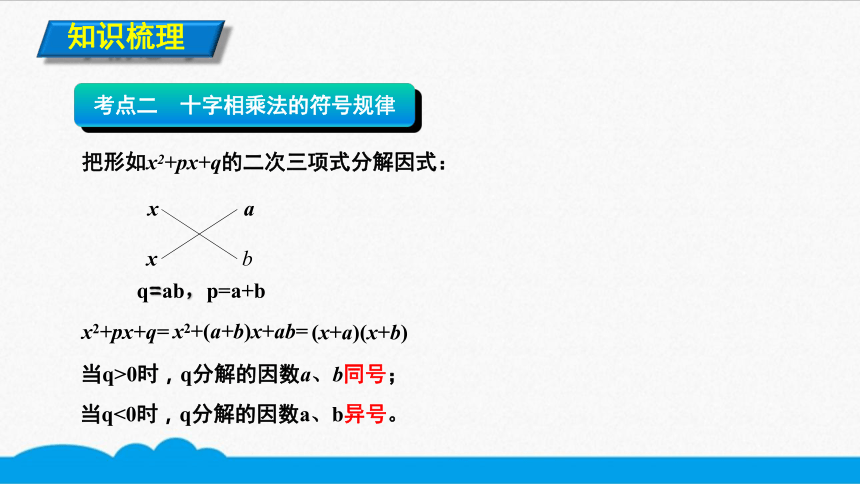
考点二 十字相乘法的符号规律
知识梳理
把形如x2+px+q的二次三项式分解因式:
当q>0时,q分解的因数a、b同号;
当q<0时,q分解的因数a、b异号。
x
x
a
b
q=ab,p=a+b
x2+px+q=
x2+(a+b)x+ab=
(x+a)(x+b)
典例剖析
形如x2+px+q的二次三项式分解因式,利用十字相乘法。运用时,需要注意拆分时数的搭配,以及一次项的系数,来保证因式分解的正确性。
方法点拨
把下列各式因式分解:
1、x?+8x+12
2、x?+4x-12
6
2
6
-2
x
x
x
x
=(x+6)(x+2)
=(x+6)(x-2)
备考技法
1.十字分解法注意:因式分解时,不但要注意首尾分解,而且还要观察一次项的系数,这样才能保证因式分解的正确性。
2.十字相乘法顺口溜:竖分常数交叉乘,横写因式不能乱。
3.十字相乘法要领:头尾分解,交叉相乘,求和凑中,观察试验。
十字相乘法
记法:竖分常数交叉乘,横写因式不能乱。
定义:利用十字交叉线来分解系数。
符号规律:①q>0时,a、b同号;②q<0时,a、b异号。
头尾分解,交叉相乘,
求和凑中,观察试验。
思维导图
元申小课 必有收获
十字相乘法
考点聚焦
1. 要求:掌握十字相乘的方法,灵活进行因式分解;
2. 形式:考题多填空形式出现;
3. 联系:整式乘法,分式化简,代数式恒等变形。
考点一 十字相乘法
知识梳理
定义:
利用十字交叉线来分解系数,把二次三项式分解因式的方法叫做十字相乘法。
步骤:
1、竖分二次项与常数项;
2、交叉相乘,和相加;
3、检验确定,横写因式。
考点二 十字相乘法的符号规律
知识梳理
把形如x2+px+q的二次三项式分解因式:
当q>0时,q分解的因数a、b同号;
当q<0时,q分解的因数a、b异号。
x
x
a
b
q=ab,p=a+b
x2+px+q=
x2+(a+b)x+ab=
(x+a)(x+b)
典例剖析
形如x2+px+q的二次三项式分解因式,利用十字相乘法。运用时,需要注意拆分时数的搭配,以及一次项的系数,来保证因式分解的正确性。
方法点拨
把下列各式因式分解:
1、x?+8x+12
2、x?+4x-12
6
2
6
-2
x
x
x
x
=(x+6)(x+2)
=(x+6)(x-2)
备考技法
1.十字分解法注意:因式分解时,不但要注意首尾分解,而且还要观察一次项的系数,这样才能保证因式分解的正确性。
2.十字相乘法顺口溜:竖分常数交叉乘,横写因式不能乱。
3.十字相乘法要领:头尾分解,交叉相乘,求和凑中,观察试验。
十字相乘法
记法:竖分常数交叉乘,横写因式不能乱。
定义:利用十字交叉线来分解系数。
符号规律:①q>0时,a、b同号;②q<0时,a、b异号。
头尾分解,交叉相乘,
求和凑中,观察试验。
思维导图
元申小课 必有收获
