初数七上 知识点精讲 42 余角和补角 课件(共10张PPT)
文档属性
| 名称 | 初数七上 知识点精讲 42 余角和补角 课件(共10张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 646.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-08 08:36:13 | ||
图片预览



文档简介
余角和补角
考点聚焦
1. 重点:角的互余、互补关系及其性质;
2. 难点:余角、补角的性质 。
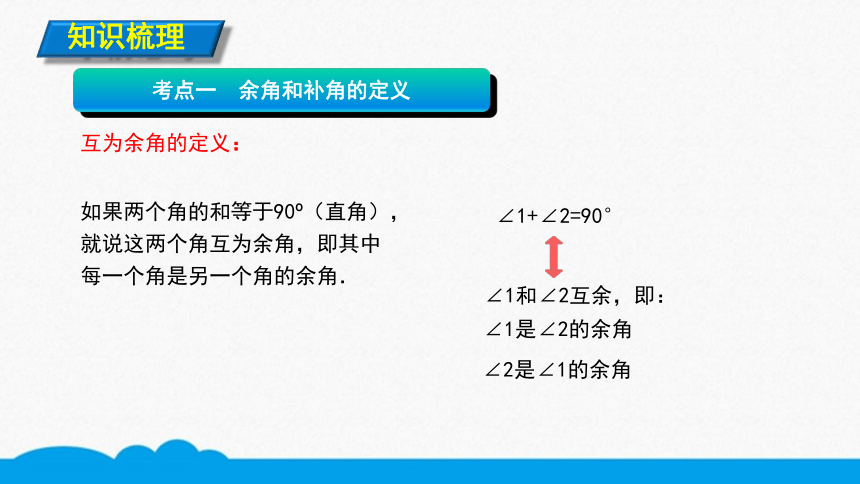
互为余角的定义:
知识梳理
考点一 余角和补角的定义
∠1+∠2=90°
∠1和∠2互余,即:
∠1是∠2的余角
∠2是∠1的余角
如果两个角的和等于90?(直角),就说这两个角互为余角,即其中每一个角是另一个角的余角.
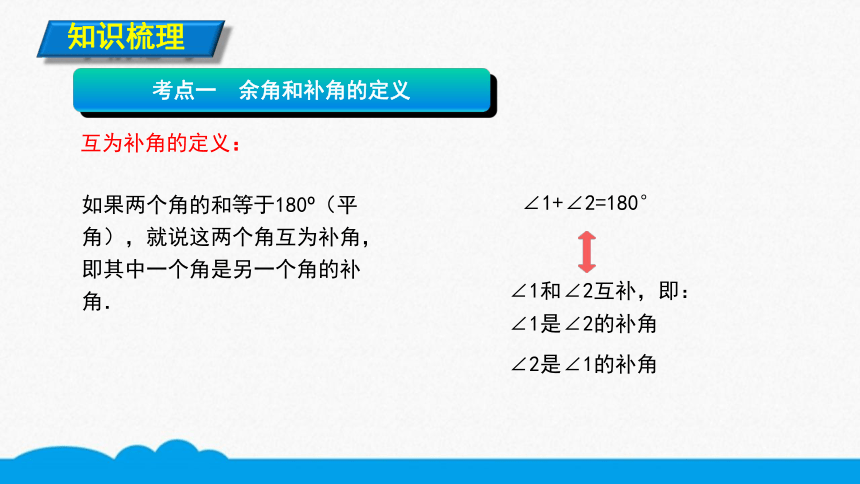
互为补角的定义:
知识梳理
考点一 余角和补角的定义
∠1和∠2互补,即:
∠1是∠2的补角
∠2是∠1的补角
如果两个角的和等于180?(平角),就说这两个角互为补角,即其中一个角是另一个角的补角.
∠1+∠2=180°
注意:
知识梳理
考点一 余角和补角的定义
1、定义中的“互为”是指每一个角都是另一个角的余角(补角)
2、补角和余角都是表示角度的大小关系,与位置无关.
若一个角的补角等于它的余角的 4 倍,求这个角的度数.
典例剖析
直接求解有困难时,可以列方程;注意补角和余角要表示正确。
方法点拨
解: 设这个角是x °,
则它的补角是( 180°-x°),余角是(90°-x°) .
根据题意得:(180°-x°)= 4 (90°-x°)
解得:x =60
答:这个角的度数是60 °.
补角的性质:
知识梳理
考点二 余角和补角的性质
同角(等角)的余角相等。
同角(等角)的补角相等。
余角的性质:
如图,∠AOD =∠BOC =90°.请问∠1与∠3,∠DOC 和∠AOB 有什么关系?并说明理由.
典例剖析
该图形中的两个直角处于叠置的位置关系,不重叠的角相等,重叠的角与大角互补。
方法点拨
解: 因为∠1与∠2互余, ∠3与∠2互余,
所以∠1=∠3.
∠DOC +∠AOB =∠2+∠1+∠2+∠3=90°+90°=180°
所以∠DOC 和∠AOB互补
备考技法
1、余角、补角的定义:
如果两个角的和等于90?(直角),就说这两个角互为余角,即其中每一个角是另一个角的余角.
如果两个角的和等于180?(平角),就说这两个角互为补角,即其中一个角是另一个角的补角
2、余角、补角的性质:
同角(等角)的补角相等;同角(等角)的余角相等。
余角和补角
余角、补角的性质。
余角、补角的定义
思维导图
都是表示角度的大小
关系,与位置无关
考点聚焦
1. 重点:角的互余、互补关系及其性质;
2. 难点:余角、补角的性质 。
互为余角的定义:
知识梳理
考点一 余角和补角的定义
∠1+∠2=90°
∠1和∠2互余,即:
∠1是∠2的余角
∠2是∠1的余角
如果两个角的和等于90?(直角),就说这两个角互为余角,即其中每一个角是另一个角的余角.
互为补角的定义:
知识梳理
考点一 余角和补角的定义
∠1和∠2互补,即:
∠1是∠2的补角
∠2是∠1的补角
如果两个角的和等于180?(平角),就说这两个角互为补角,即其中一个角是另一个角的补角.
∠1+∠2=180°
注意:
知识梳理
考点一 余角和补角的定义
1、定义中的“互为”是指每一个角都是另一个角的余角(补角)
2、补角和余角都是表示角度的大小关系,与位置无关.
若一个角的补角等于它的余角的 4 倍,求这个角的度数.
典例剖析
直接求解有困难时,可以列方程;注意补角和余角要表示正确。
方法点拨
解: 设这个角是x °,
则它的补角是( 180°-x°),余角是(90°-x°) .
根据题意得:(180°-x°)= 4 (90°-x°)
解得:x =60
答:这个角的度数是60 °.
补角的性质:
知识梳理
考点二 余角和补角的性质
同角(等角)的余角相等。
同角(等角)的补角相等。
余角的性质:
如图,∠AOD =∠BOC =90°.请问∠1与∠3,∠DOC 和∠AOB 有什么关系?并说明理由.
典例剖析
该图形中的两个直角处于叠置的位置关系,不重叠的角相等,重叠的角与大角互补。
方法点拨
解: 因为∠1与∠2互余, ∠3与∠2互余,
所以∠1=∠3.
∠DOC +∠AOB =∠2+∠1+∠2+∠3=90°+90°=180°
所以∠DOC 和∠AOB互补
备考技法
1、余角、补角的定义:
如果两个角的和等于90?(直角),就说这两个角互为余角,即其中每一个角是另一个角的余角.
如果两个角的和等于180?(平角),就说这两个角互为补角,即其中一个角是另一个角的补角
2、余角、补角的性质:
同角(等角)的补角相等;同角(等角)的余角相等。
余角和补角
余角、补角的性质。
余角、补角的定义
思维导图
都是表示角度的大小
关系,与位置无关
