七年级数学7.3 多边形的内角和说课课件
文档属性
| 名称 | 七年级数学7.3 多边形的内角和说课课件 |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-26 19:46:41 | ||
图片预览










文档简介
(共55张PPT)
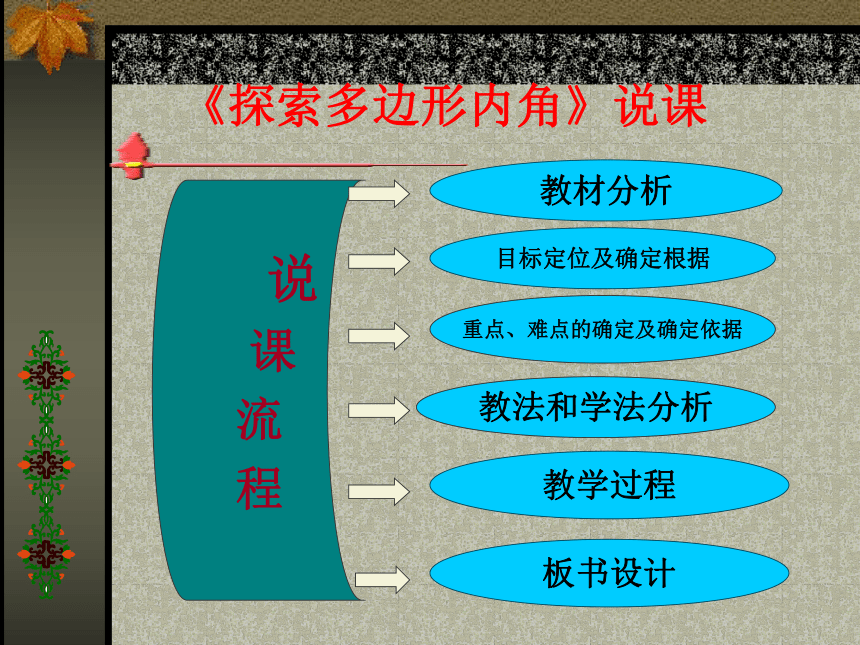
《探索多边形内角》说课
说
课
流
程
教材分析
目标定位及确定根据
教学过程
板书设计
重点、难点的确定及确定依据
教法和学法分析
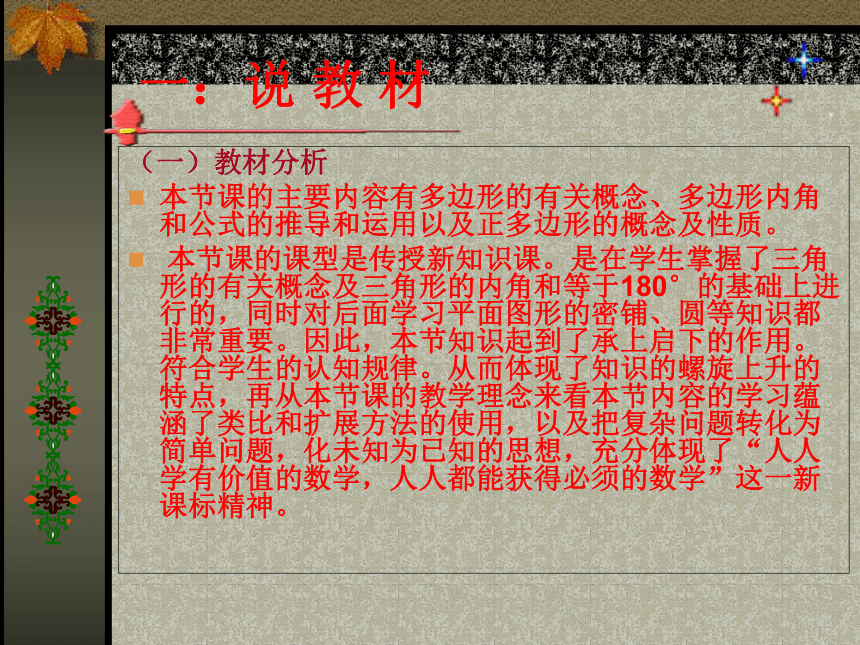
一:说 教 材
(一)教材分析
本节课的主要内容有多边形的有关概念、多边形内角和公式的推导和运用以及正多边形的概念及性质。
本节课的课型是传授新知识课。是在学生掌握了三角形的有关概念及三角形的内角和等于180°的基础上进行的,同时对后面学习平面图形的密铺、圆等知识都非常重要。因此,本节知识起到了承上启下的作用。符合学生的认知规律。从而体现了知识的螺旋上升的特点,再从本节课的教学理念来看本节内容的学习蕴涵了类比和扩展方法的使用,以及把复杂问题转化为简单问题,化未知为已知的思想,充分体现了“人人学有价值的数学,人人都能获得必须的数学”这一新课标精神。
目标定位及确定根据。
基于对教材的理解和分析,教材目标是使学生由不知到认识到乐知的升华过程。依据《课标》要求,我设立了如下的三维目标。
二:说 目标
1、知识与技能的目标:
①认识多边形
②通过动手实践,探究思索,交流互助。能将
多边形问题转化为三角形问题。从而深刻理解
多边形内角和公式的推导,并会加以运用。
二:说目标
2、过程与方法目标:
经历直观感知、探索、归纳,应用创新的过程,培养学生的实践能力,协作能力及创新意识。
3、情感、态度与价值观目标:
培养学生的参与意识和集体主义观念。
三:说重难点
重点、难点的确定及确定依据。
本节课的重点是多边形内角和的探索。使学生由感性认识过渡到感性与理性相融。根据以往的教学经验,学生在几何的逻辑推理上感到有难度,所以我确定本节课的难点是探究多边形内角和公式,即将多边形问题转化为三角形问题来解决的基本思想。而解决问题的关键是恰当的引导学生实施转化过程。
四.说 教 法 和 学 法 指 导
新课标要求“不仅要关注学生的学习结果,更要关注他们学习的过程,体验数学与生活的联系”.本节课的概念,公式,结论等教学中,若能让学生自己去发现概念形成的过程,自己动手实践推导出公式, 体验学与用乐趣,则更能增进学生学好数学用好数学的信心.所以我制定了以下的教法和学法指导:
【教学方法】 类比教学 情景探究
启发激励 师生互动
【学法指导】自主探究 动手实践
合作交流 归纳验证
五.教 学 过 程 设 计
作业布置
小组活动,领悟新知
自主学习、知识提炼
直观演示,引入新课
应用举例,深化理解
课堂初练 在露锋芒
一.激情导入直观演示,引入新课得出多边形的有关概念
古埃及金字塔
风景秀丽的曼哈顿
美国国防部大楼——五角大楼
中国第一奇村诸葛八卦村
生活中的平面图形
生活中的平面图形
由这图形你抽象出什么几何图形?
三角形
生活中的平面图形
由这图形你抽象出什么几何图形?
长方形
生活中的平面图形
由这图形你抽象出什么几何图形?
菱形
生活中的平面图形
由这图形你抽象出什么几何图形?
六边形
生活中的平面图形
由这图形你抽象出什么几何图形?
五边形
设计意图
这样直观而又丰富多彩的素材使学生由无意注意到有意注意,构起对现实世界中已有知识的回忆与联想,体会几何图形的形体美从而激发学生学习的兴趣与探究的热情。
自主学习、知识提炼
在学生顺利找出三角形、正方形、长方形,并且发现任意四边形及五边形后,趁势引导学生复习三角形概念,为学生类比学习多边形的概念作好铺垫。指出以上这些图形都叫多边形。此时,我板书课题:多边形,让学生明确学习的一个重点知识是认识多边形。要求学生通过观察以上图形,自主探索归纳得到多边形的概念,学生可能归纳的不完善,通常在三角形概念的对比下会丢掉“在平而内”的条件要加以强调。
三角形
长方形
六边形
四边形
八边形
在同一平面内,由一些不在同一条直线上的线段首尾顺次相接组成的图形叫做多边形。
多边形的定义
你能仿照三角形的定义给出多边形的定义吗?
在同一平面内,由不在同一条直线上的三条线段
首尾顺次相接组成的图形叫做三角形
之后,就要求学生自学课本中提出的多边形相关概念。我以五边形为例检验学生所学知识是否到位,培养学生的自学能力,理解能力,我重点检查学生对多边形的表示及对角线的理解。然后通过引导让学生明白从n边形的一个顶点出发可以引(n-3)条对角线, 把多边形分成(n-2)个三角形。
了解一下
内角
对角线
对角线:连接多边形不相邻的两个顶点的线段叫做对角线。
可表示为:五边形ABCDE或五边形AEDCB
A
B
C
D
E
外角
1
随后我指出凸多边形及凹多边形,并用多媒体课件演示,让学生会区别两种图形,并指出我们暂时只研究凸多边形。
比一比.画一画
请分别画出下列两个图形各边所在的直线,你能
得到什么结论?
(1)
(2)
如图(1)这样,画出多边形的任何一条边所在的直线,整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形。本节我们只讨论凸多边形。
A
B
C
D
E
F
G
H
我们一起学习了多边形相关概念,多边形的内角和又是多少?然后,用多媒体展示美丽壮观的中心广场。提出问题:上图是通江县中心广场规划图片它的边缘是一个五边形,你能设法求出它的五个内角的和吗?与同伴交流,并提出探究要求。我补充课题为:探索多边形的内角和。
上图中广场中心的边缘是一个五边形,
你能设法求出它的五个内角的和吗?
二、小组合作,领悟新知
要求:在纸板上画一个五边形,然
后想法用手头上的工具算出或测出
它的内角和,小组内合作完成!
设计意图
再一次用直观而丰富的素材使学生由无意注意到有意注意。同时让学生体会到几何图形的实用性。也为下节课做了影射。从实际问题中抽象出数学模型——五边形,要求学生画出五边形,利用手中的工具想办法求其内角和。给学生充足的时间思考后学生会想到度量法,剪切拼凑法也有想到连对角线的。让学生不由自主的动起来,在动中思考,在动中交流,在动中将每个知识自然而然的发现。倡导个性化学习
分类检查,突破难关!
当学生分小组探究出各种不同的方法后,进行分类检查。提问:小明、小亮、小东、小华分别利用下面的图形求出了该五边形的五个内角的和(多媒体展示),谁和小明的方法相同说说你的理由?再分小组抽查小亮,小东,小华的方法。
小明、小亮、小东、小华分别是这样做的
小明
小亮
小华
小东
在图形的引导下,学生不难求出五边形内角和,我适时引导学生得出他们的共同思路是将五边形转化为三角形。
设计意图:这样设计,可以使学生以强烈的求知欲和饱满的热情学习新知。利用多媒体展示图形让学生直观性的理解知识,突破学生的思维瓶颈,有利地培养学生大胆的探索精神,多元化思维能力和集体感。
趁胜追击,攻破难关!
接着我提出问题:六边形、七边形的内角和可用上述各种方法求吗?由于学生思维已经可以正迁移了,要求学生利用最简单的方法①和②探究六边形、七边形、n边形(n≥3)能分割成三角形的个数,并填好引导表,从而探索得到n边形内角和公式:(n-2)·180°。
你能利用方法①和②探究六边形、七边形、n边形(n≥3)的内角和吗?
多边形 内角和
4× = ( - 2)×
5× =( - 2) ×
( -2) ×
方法①
6
7
n
方法②
多边形 内角和
6× - = ×( -2)
7× - = ×( -2)
n× - = ×( -2)
6
7
n
6边形
7边形
n边形
6边形
7边形
n边形
设计意图:
这样引导学生从简单、特殊的图形入手,利用熟悉的三角形内角和,把未知的转化为已知的,逐步归纳得出多边形的内角和公式,向学生渗透从特殊到一般、从具体到抽象的辨证思想和方法。同时,轻松突破本节难点。
应用举例,深化理解
例. 已知一个多边形,它的内角和 等于五边形内角和的2倍,求这个多边形的边数。
设计意图:使学习的知识要得到
及时巩固、加深理解和记忆,活
学活用显我真本。
课堂练笔!
1、九边形的内角和是________
2、从多边形的一个顶点所引的对角线把这个多边形分成了5个三角形,那么这个三角形是___边形,内角和为_____.。
3.多边形的边数每增加一边,它的内角和增加_____。
4、一个多边形的内角和等于1440°,那么它是______边形。
5.2008年北京奥运,有同学为了庆祝奥运会,想设计一个内角和为2008度的多边形,他能实现这个愿望吗?为什么?
1、一个多边形的每一个内角都等于
135 ,则它是____边形. 2、考考你:有一张长方形的木板面,
它的四个内角和为360度,现在锯掉
它的一个角,剩下残余木板面所有的
内角和是多少?
设计意图
典型的题目由浅入深,阶梯性出现,紧扣多边形内角和公式的运用,有利于知识的掌握。让学生对多边形内角和公式有更深刻的理解。两组习题的安排体现了课改精神,面向全体,遵循巩固与发展相结合的原则,培养创新意识。既能锻炼能力强的学生,又能照顾能力弱的学生,可调动不同层次学生的积极性。
小 结
我们探究了多边形的内角和公式
(n-2) ×180°。
从n边形的一个顶点出发
可以引(n-3)条对角线,
把多边形分成(n-2)个三角形。
我们在研究、探索多边形的内角和公式时,首先从具体的、特殊的四边形、五边形入手,来得出多边形的内角和公式。在研究问题的过程中,把多边形问题通过分割成三角形来研究,即把复杂问题转化为简单问题,利用旧知识解决新问题,这种研究和探索问题的方法都是我们在学习数学过程中,经常要用到的,希望同学们要领悟这种思想方法。
六.课后作业及实践:
(一)必做题
1.课本P71习题第2题
2.已知一个多边形的每个内角为156度
则 这个多边形是多少边形?
(二)选做题
1.设计一个实验,说明四边形内角和是
360°
2.一个多边形除去一个内角外其余内角之和等于750度这个内角等于多少度?
(三)课外思考:
什么是正多边形?探索多边形的外角和
板书设计:
一、
①多边形的概念 n边形(n≥3,n为正整数)
过n边形每一个顶点可做(n-3)条对角线
把n边形分成了(n-20)个三角形
②多边形内角和的探究
③多边形的内角和:(n-2)·180°
二、例题
《探索多边形内角》说课
说
课
流
程
教材分析
目标定位及确定根据
教学过程
板书设计
重点、难点的确定及确定依据
教法和学法分析
一:说 教 材
(一)教材分析
本节课的主要内容有多边形的有关概念、多边形内角和公式的推导和运用以及正多边形的概念及性质。
本节课的课型是传授新知识课。是在学生掌握了三角形的有关概念及三角形的内角和等于180°的基础上进行的,同时对后面学习平面图形的密铺、圆等知识都非常重要。因此,本节知识起到了承上启下的作用。符合学生的认知规律。从而体现了知识的螺旋上升的特点,再从本节课的教学理念来看本节内容的学习蕴涵了类比和扩展方法的使用,以及把复杂问题转化为简单问题,化未知为已知的思想,充分体现了“人人学有价值的数学,人人都能获得必须的数学”这一新课标精神。
目标定位及确定根据。
基于对教材的理解和分析,教材目标是使学生由不知到认识到乐知的升华过程。依据《课标》要求,我设立了如下的三维目标。
二:说 目标
1、知识与技能的目标:
①认识多边形
②通过动手实践,探究思索,交流互助。能将
多边形问题转化为三角形问题。从而深刻理解
多边形内角和公式的推导,并会加以运用。
二:说目标
2、过程与方法目标:
经历直观感知、探索、归纳,应用创新的过程,培养学生的实践能力,协作能力及创新意识。
3、情感、态度与价值观目标:
培养学生的参与意识和集体主义观念。
三:说重难点
重点、难点的确定及确定依据。
本节课的重点是多边形内角和的探索。使学生由感性认识过渡到感性与理性相融。根据以往的教学经验,学生在几何的逻辑推理上感到有难度,所以我确定本节课的难点是探究多边形内角和公式,即将多边形问题转化为三角形问题来解决的基本思想。而解决问题的关键是恰当的引导学生实施转化过程。
四.说 教 法 和 学 法 指 导
新课标要求“不仅要关注学生的学习结果,更要关注他们学习的过程,体验数学与生活的联系”.本节课的概念,公式,结论等教学中,若能让学生自己去发现概念形成的过程,自己动手实践推导出公式, 体验学与用乐趣,则更能增进学生学好数学用好数学的信心.所以我制定了以下的教法和学法指导:
【教学方法】 类比教学 情景探究
启发激励 师生互动
【学法指导】自主探究 动手实践
合作交流 归纳验证
五.教 学 过 程 设 计
作业布置
小组活动,领悟新知
自主学习、知识提炼
直观演示,引入新课
应用举例,深化理解
课堂初练 在露锋芒
一.激情导入直观演示,引入新课得出多边形的有关概念
古埃及金字塔
风景秀丽的曼哈顿
美国国防部大楼——五角大楼
中国第一奇村诸葛八卦村
生活中的平面图形
生活中的平面图形
由这图形你抽象出什么几何图形?
三角形
生活中的平面图形
由这图形你抽象出什么几何图形?
长方形
生活中的平面图形
由这图形你抽象出什么几何图形?
菱形
生活中的平面图形
由这图形你抽象出什么几何图形?
六边形
生活中的平面图形
由这图形你抽象出什么几何图形?
五边形
设计意图
这样直观而又丰富多彩的素材使学生由无意注意到有意注意,构起对现实世界中已有知识的回忆与联想,体会几何图形的形体美从而激发学生学习的兴趣与探究的热情。
自主学习、知识提炼
在学生顺利找出三角形、正方形、长方形,并且发现任意四边形及五边形后,趁势引导学生复习三角形概念,为学生类比学习多边形的概念作好铺垫。指出以上这些图形都叫多边形。此时,我板书课题:多边形,让学生明确学习的一个重点知识是认识多边形。要求学生通过观察以上图形,自主探索归纳得到多边形的概念,学生可能归纳的不完善,通常在三角形概念的对比下会丢掉“在平而内”的条件要加以强调。
三角形
长方形
六边形
四边形
八边形
在同一平面内,由一些不在同一条直线上的线段首尾顺次相接组成的图形叫做多边形。
多边形的定义
你能仿照三角形的定义给出多边形的定义吗?
在同一平面内,由不在同一条直线上的三条线段
首尾顺次相接组成的图形叫做三角形
之后,就要求学生自学课本中提出的多边形相关概念。我以五边形为例检验学生所学知识是否到位,培养学生的自学能力,理解能力,我重点检查学生对多边形的表示及对角线的理解。然后通过引导让学生明白从n边形的一个顶点出发可以引(n-3)条对角线, 把多边形分成(n-2)个三角形。
了解一下
内角
对角线
对角线:连接多边形不相邻的两个顶点的线段叫做对角线。
可表示为:五边形ABCDE或五边形AEDCB
A
B
C
D
E
外角
1
随后我指出凸多边形及凹多边形,并用多媒体课件演示,让学生会区别两种图形,并指出我们暂时只研究凸多边形。
比一比.画一画
请分别画出下列两个图形各边所在的直线,你能
得到什么结论?
(1)
(2)
如图(1)这样,画出多边形的任何一条边所在的直线,整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形。本节我们只讨论凸多边形。
A
B
C
D
E
F
G
H
我们一起学习了多边形相关概念,多边形的内角和又是多少?然后,用多媒体展示美丽壮观的中心广场。提出问题:上图是通江县中心广场规划图片它的边缘是一个五边形,你能设法求出它的五个内角的和吗?与同伴交流,并提出探究要求。我补充课题为:探索多边形的内角和。
上图中广场中心的边缘是一个五边形,
你能设法求出它的五个内角的和吗?
二、小组合作,领悟新知
要求:在纸板上画一个五边形,然
后想法用手头上的工具算出或测出
它的内角和,小组内合作完成!
设计意图
再一次用直观而丰富的素材使学生由无意注意到有意注意。同时让学生体会到几何图形的实用性。也为下节课做了影射。从实际问题中抽象出数学模型——五边形,要求学生画出五边形,利用手中的工具想办法求其内角和。给学生充足的时间思考后学生会想到度量法,剪切拼凑法也有想到连对角线的。让学生不由自主的动起来,在动中思考,在动中交流,在动中将每个知识自然而然的发现。倡导个性化学习
分类检查,突破难关!
当学生分小组探究出各种不同的方法后,进行分类检查。提问:小明、小亮、小东、小华分别利用下面的图形求出了该五边形的五个内角的和(多媒体展示),谁和小明的方法相同说说你的理由?再分小组抽查小亮,小东,小华的方法。
小明、小亮、小东、小华分别是这样做的
小明
小亮
小华
小东
在图形的引导下,学生不难求出五边形内角和,我适时引导学生得出他们的共同思路是将五边形转化为三角形。
设计意图:这样设计,可以使学生以强烈的求知欲和饱满的热情学习新知。利用多媒体展示图形让学生直观性的理解知识,突破学生的思维瓶颈,有利地培养学生大胆的探索精神,多元化思维能力和集体感。
趁胜追击,攻破难关!
接着我提出问题:六边形、七边形的内角和可用上述各种方法求吗?由于学生思维已经可以正迁移了,要求学生利用最简单的方法①和②探究六边形、七边形、n边形(n≥3)能分割成三角形的个数,并填好引导表,从而探索得到n边形内角和公式:(n-2)·180°。
你能利用方法①和②探究六边形、七边形、n边形(n≥3)的内角和吗?
多边形 内角和
4× = ( - 2)×
5× =( - 2) ×
( -2) ×
方法①
6
7
n
方法②
多边形 内角和
6× - = ×( -2)
7× - = ×( -2)
n× - = ×( -2)
6
7
n
6边形
7边形
n边形
6边形
7边形
n边形
设计意图:
这样引导学生从简单、特殊的图形入手,利用熟悉的三角形内角和,把未知的转化为已知的,逐步归纳得出多边形的内角和公式,向学生渗透从特殊到一般、从具体到抽象的辨证思想和方法。同时,轻松突破本节难点。
应用举例,深化理解
例. 已知一个多边形,它的内角和 等于五边形内角和的2倍,求这个多边形的边数。
设计意图:使学习的知识要得到
及时巩固、加深理解和记忆,活
学活用显我真本。
课堂练笔!
1、九边形的内角和是________
2、从多边形的一个顶点所引的对角线把这个多边形分成了5个三角形,那么这个三角形是___边形,内角和为_____.。
3.多边形的边数每增加一边,它的内角和增加_____。
4、一个多边形的内角和等于1440°,那么它是______边形。
5.2008年北京奥运,有同学为了庆祝奥运会,想设计一个内角和为2008度的多边形,他能实现这个愿望吗?为什么?
1、一个多边形的每一个内角都等于
135 ,则它是____边形. 2、考考你:有一张长方形的木板面,
它的四个内角和为360度,现在锯掉
它的一个角,剩下残余木板面所有的
内角和是多少?
设计意图
典型的题目由浅入深,阶梯性出现,紧扣多边形内角和公式的运用,有利于知识的掌握。让学生对多边形内角和公式有更深刻的理解。两组习题的安排体现了课改精神,面向全体,遵循巩固与发展相结合的原则,培养创新意识。既能锻炼能力强的学生,又能照顾能力弱的学生,可调动不同层次学生的积极性。
小 结
我们探究了多边形的内角和公式
(n-2) ×180°。
从n边形的一个顶点出发
可以引(n-3)条对角线,
把多边形分成(n-2)个三角形。
我们在研究、探索多边形的内角和公式时,首先从具体的、特殊的四边形、五边形入手,来得出多边形的内角和公式。在研究问题的过程中,把多边形问题通过分割成三角形来研究,即把复杂问题转化为简单问题,利用旧知识解决新问题,这种研究和探索问题的方法都是我们在学习数学过程中,经常要用到的,希望同学们要领悟这种思想方法。
六.课后作业及实践:
(一)必做题
1.课本P71习题第2题
2.已知一个多边形的每个内角为156度
则 这个多边形是多少边形?
(二)选做题
1.设计一个实验,说明四边形内角和是
360°
2.一个多边形除去一个内角外其余内角之和等于750度这个内角等于多少度?
(三)课外思考:
什么是正多边形?探索多边形的外角和
板书设计:
一、
①多边形的概念 n边形(n≥3,n为正整数)
过n边形每一个顶点可做(n-3)条对角线
把n边形分成了(n-20)个三角形
②多边形内角和的探究
③多边形的内角和:(n-2)·180°
二、例题
