相似三角形的判定1(边边边与边角边)
文档属性
| 名称 | 相似三角形的判定1(边边边与边角边) |
|
|
| 格式 | zip | ||
| 文件大小 | 177.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-26 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
1. 对应角_______, 对应边——————的两个三角形,叫做相似三角形 .
相等
成比例
2. 相似三角形的———————, 各对应边——————。
对应角相等
成比例
3.如何识别两三角形是否相似
∵ DE∥BC
∴ △ ADE ∽ △ ABC
平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
D
E
O
B
C
A
B
C
D
E
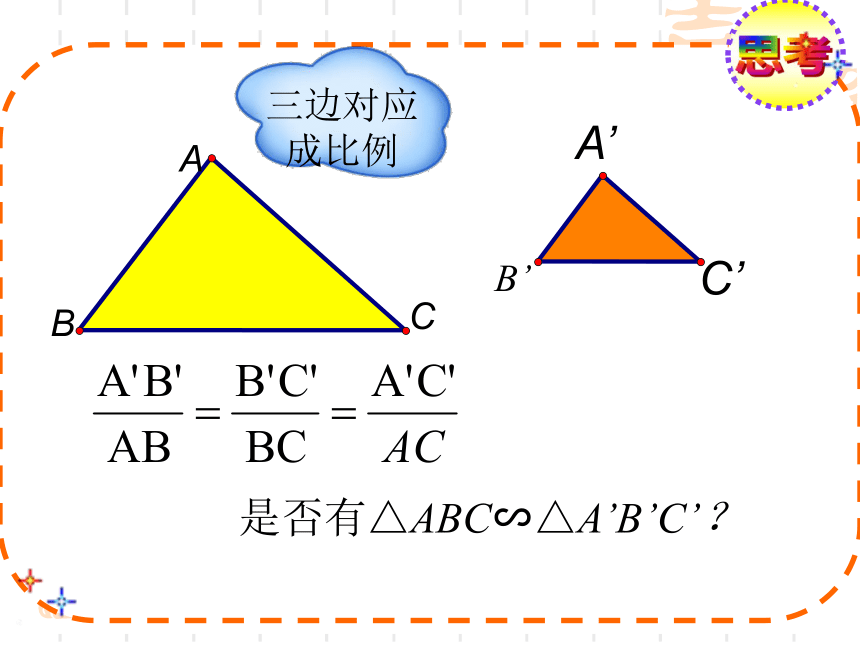
思考:有没有其他简单的办法判断两个三角形相似
是否有△ABC∽△A’B’C’?
A
B
C
C’
B’
A’
三边对应成比例
A
B
C
C’
B’
A’
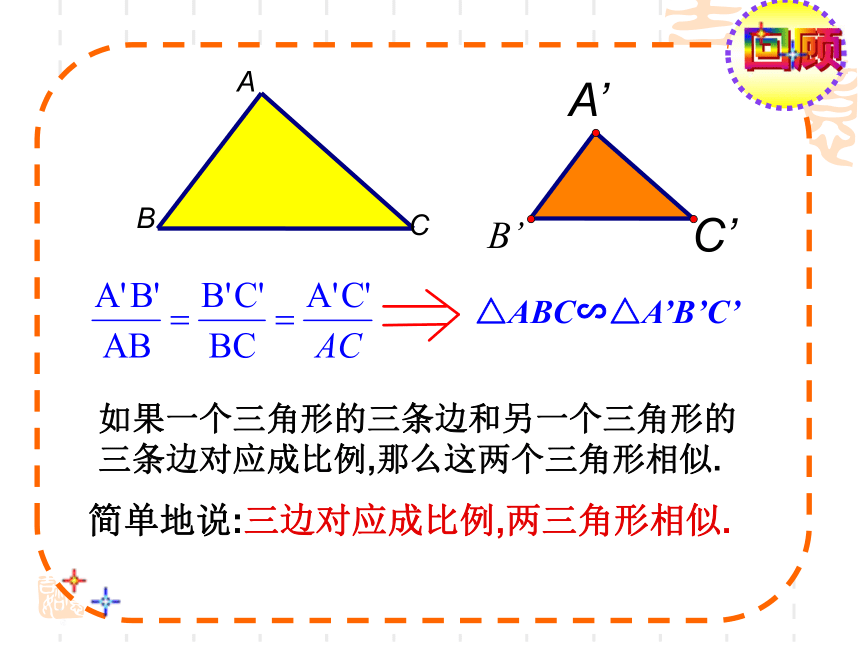
△ABC∽△A’B’C’
如果一个三角形的三条边和另一个三角形的三条边对应成比例,那么这两个三角形相似.
简单地说:三边对应成比例,两三角形相似.
例1:在△ABC和△A′B′C′中,已知:
(1)AB=6 cm, BC=8 cm,AC=10 cm,
A′B′=18 cm,B′C′=24 cm,A′C′=30 cm.
试判定△ABC与A′B′C′是否相似,并说明理由.
(2) AB=12cm, BC=15cm, AC=24cm
A’B’=16cm,B’C’=20cm,A’C’=30cm
判断两个三角形相似,你有哪些方法
方法1:通过定义(不常用)
方法2:通过平行线。
方法3:三边对应成比例。
如果有一点E在边AC上,那么点E应该在什么位置才能使△ADE∽△ABC相似呢?
此时,
如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形一定相似吗?
E
=?
已知:如图△ABC和△A`B`C`中,∠A=∠A` , ∠A` ,A`B`:AB=A`C`:AC.
求证:△ABC∽△A`B`C`
A`
B`
C`
A
B
C
E
D
证明:在△ABC的边AB、AC(或它们的延长线)
上分别截取AD=A`B`,AE=A`C`,连结DE.
∠A=∠A`, 这样,△ADE≌△A`B`C`.
∵A`B`:AB=A`C`:AC
∴ AD:AB=AE:AC
∴DE∥BC
∴△ADE∽△ABC
∴△A`B`C`∽△ABC
相似三角形的识别
∴△ABC∽△
如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似 。
(两边对应成比例且夹角相等,两三角形相似)
A
B
C
A′
B′
C′
想一想:如果对应相等的角不是两条对应边的夹角,那么两个三角形是否相似呢?
A
B
C
D
E
F
1、已知△ABC和 △A’B’C’,根据下列条件
判断它们是否相似.
(2) ∠A=45°,AB=12cm, AC=15cm
∠A’=45°,A’B’=16cm,A’C’=20cm
(1)∠A=120°,AB=7cm,AC=14cm,
∠A`=120°,A`B`=3cm,A`C`=6cm;
∵ = =1.5
2、判断图中△AEB和△FEC是否相似?
解:
∴△AEB∽△FEC
∵∠1=∠2
= =1.5
∴ =
54
30
36
45
E
A
F
C
B
1
2
平行于三角形一边的直线与其他两边(或延长线)相交,所构成的三角形与原三角形相似;
三边对应成比例,两三角形相似.
相似三角形的判定方法
两边对应成比例且夹角相等,两三角形相似.
1. 对应角_______, 对应边——————的两个三角形,叫做相似三角形 .
相等
成比例
2. 相似三角形的———————, 各对应边——————。
对应角相等
成比例
3.如何识别两三角形是否相似
∵ DE∥BC
∴ △ ADE ∽ △ ABC
平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
D
E
O
B
C
A
B
C
D
E
思考:有没有其他简单的办法判断两个三角形相似
是否有△ABC∽△A’B’C’?
A
B
C
C’
B’
A’
三边对应成比例
A
B
C
C’
B’
A’
△ABC∽△A’B’C’
如果一个三角形的三条边和另一个三角形的三条边对应成比例,那么这两个三角形相似.
简单地说:三边对应成比例,两三角形相似.
例1:在△ABC和△A′B′C′中,已知:
(1)AB=6 cm, BC=8 cm,AC=10 cm,
A′B′=18 cm,B′C′=24 cm,A′C′=30 cm.
试判定△ABC与A′B′C′是否相似,并说明理由.
(2) AB=12cm, BC=15cm, AC=24cm
A’B’=16cm,B’C’=20cm,A’C’=30cm
判断两个三角形相似,你有哪些方法
方法1:通过定义(不常用)
方法2:通过平行线。
方法3:三边对应成比例。
如果有一点E在边AC上,那么点E应该在什么位置才能使△ADE∽△ABC相似呢?
此时,
如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形一定相似吗?
E
=?
已知:如图△ABC和△A`B`C`中,∠A=∠A` , ∠A` ,A`B`:AB=A`C`:AC.
求证:△ABC∽△A`B`C`
A`
B`
C`
A
B
C
E
D
证明:在△ABC的边AB、AC(或它们的延长线)
上分别截取AD=A`B`,AE=A`C`,连结DE.
∠A=∠A`, 这样,△ADE≌△A`B`C`.
∵A`B`:AB=A`C`:AC
∴ AD:AB=AE:AC
∴DE∥BC
∴△ADE∽△ABC
∴△A`B`C`∽△ABC
相似三角形的识别
∴△ABC∽△
如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似 。
(两边对应成比例且夹角相等,两三角形相似)
A
B
C
A′
B′
C′
想一想:如果对应相等的角不是两条对应边的夹角,那么两个三角形是否相似呢?
A
B
C
D
E
F
1、已知△ABC和 △A’B’C’,根据下列条件
判断它们是否相似.
(2) ∠A=45°,AB=12cm, AC=15cm
∠A’=45°,A’B’=16cm,A’C’=20cm
(1)∠A=120°,AB=7cm,AC=14cm,
∠A`=120°,A`B`=3cm,A`C`=6cm;
∵ = =1.5
2、判断图中△AEB和△FEC是否相似?
解:
∴△AEB∽△FEC
∵∠1=∠2
= =1.5
∴ =
54
30
36
45
E
A
F
C
B
1
2
平行于三角形一边的直线与其他两边(或延长线)相交,所构成的三角形与原三角形相似;
三边对应成比例,两三角形相似.
相似三角形的判定方法
两边对应成比例且夹角相等,两三角形相似.
