人教版七年级数学下册7.1.2平面直角坐标系 同步练习题 (word版含答案)
文档属性
| 名称 | 人教版七年级数学下册7.1.2平面直角坐标系 同步练习题 (word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 102.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-08 11:28:27 | ||
图片预览


文档简介
第七章 平面直角坐标系
7.1.2 平面直角坐标系
1.
下列选项中,平面直角坐标系的画法正确的是( )
2.
若点A(a+2,a-1)在y轴上,那么a的值为( )
A.-2 B.2 C.-1 D.1
3.
已知|x-2|+(y+3)2=0,则P(x,y)在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
4.
P(3,-4)到x轴的距离是( )
A.2 B.3 C.4 D.5
5.
点P在第三象限内,点P到x轴的距离是4,到y轴的距离是3,那么点P的坐标为( )
A.(-4,3)
B.(-3,-4)
C.(-4,-3)
D.(3,-4)
6.已知点P(0,m)在y轴的负半轴上,则点M(-m,-m+1)在第
象限.
7.如果点M(a+b,ab)在第二象限,那么点N(a,b)在第
象限.
8.已知点P(-3,2),则P在第
象限,P到x轴的距离是
,到y轴的距离是
.
9.AB∥y轴,AB=3,若点A的坐标是(5,-4),则点B的坐标是
.
10.
如图,在平面直角坐标系中,点P的坐标为
.
11.
如图,P1、P2、P3这三个点中,在第二象限内的有
.
12.点P(a,b)满足ab>0,则点P在第
象限;点P(a,b)满足ab<0,则点P在第
象限;点P(a,b)满足ab=0,则点P在
.
13.已知点P的坐标为(3a-2,a+6),且点P到两坐标轴距离相等,则a=
.
14.
点(a+5,a-3)若在x轴上,则a的值为
,该点的坐标为
;若在y轴上,则a的值为
,该点的坐标为
.
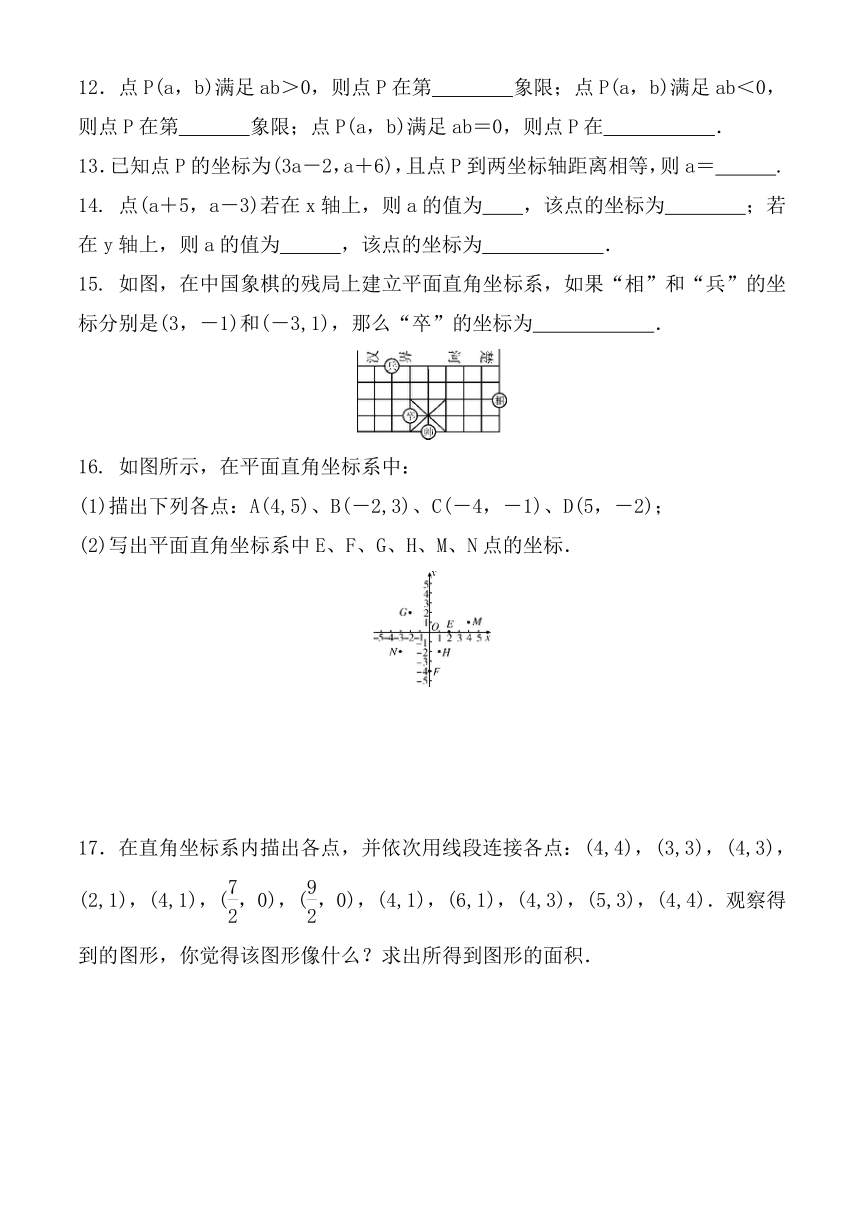
15.
如图,在中国象棋的残局上建立平面直角坐标系,如果“相”和“兵”的坐标分别是(3,-1)和(-3,1),那么“卒”的坐标为
.
16.
如图所示,在平面直角坐标系中:
(1)描出下列各点:A(4,5)、B(-2,3)、C(-4,-1)、D(5,-2);
(2)写出平面直角坐标系中E、F、G、H、M、N点的坐标.
17.在直角坐标系内描出各点,并依次用线段连接各点:(4,4),(3,3),(4,3),(2,1),(4,1),(,0),(,0),(4,1),(6,1),(4,3),(5,3),(4,4).观察得到的图形,你觉得该图形像什么?求出所得到图形的面积.
18.已知点P(a-2,2a+8),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P在y轴上;
(3)点Q的坐标为(1,5),直线PQ∥y轴;
(4)点P到x轴、y轴的距离相等.
19.
某探险家得到一幅宝藏图,海岛上四棵古树的位置分别记作A(-1,-2)、B(4,3)、C(1,6)、D(5,-2),宝藏埋在直线AB和CD的交点处.
(1)在图中画出A、B、C、D四点;
(2)连接AB、CD,写出宝藏所在地的坐标.
20.
16.在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图所示.
(1)填写下列各点的坐标:A1(
,
)、A3(
,
)、A12(
,
);
(2)写出点A4n的坐标(n是正整数);
(3)写出蚂蚁从点A100到点A101的移动方向.
答案;
1-5
BADCB
6.
一
7.
三
8.
二
2
9.
(5,-1)或(5,-7)
10.
(3,-2)
11.
P1
12.
一、三
二、四
坐标轴上
13.
4或-1
14.
3
(8,0)
-5
(0,-8)
15.
(-2,-2)
16.
解:(1)图略;
(2)E(2,0)、F(0,-4)、G(-2,2)、H(1,-2)、M(4,1)、N(-3,-2).
17.
解:如图所示
:
该图形像宝塔松.
图形的面积为:×1×1+×4×2+×2×1=+4+1=.
18.
解:(1)P(-6,0); (2)P(0,12); (3)P(1,14); (4)P(-12,-12)或(-4,4).
19.
解:(1)描点如图所示:
(2)(3,2).
20.
解:(1)A1(0,1)、A3(1,0)、A12(6,0);
(2)A4n(2n,0);
(3)点A100中的100正好是4的倍数,所以点A100和A101的坐标分别是A100(50,0)、A101(50,1),所以蚂蚁从点A100到点A101的移动方向是从下向上.
7.1.2 平面直角坐标系
1.
下列选项中,平面直角坐标系的画法正确的是( )
2.
若点A(a+2,a-1)在y轴上,那么a的值为( )
A.-2 B.2 C.-1 D.1
3.
已知|x-2|+(y+3)2=0,则P(x,y)在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
4.
P(3,-4)到x轴的距离是( )
A.2 B.3 C.4 D.5
5.
点P在第三象限内,点P到x轴的距离是4,到y轴的距离是3,那么点P的坐标为( )
A.(-4,3)
B.(-3,-4)
C.(-4,-3)
D.(3,-4)
6.已知点P(0,m)在y轴的负半轴上,则点M(-m,-m+1)在第
象限.
7.如果点M(a+b,ab)在第二象限,那么点N(a,b)在第
象限.
8.已知点P(-3,2),则P在第
象限,P到x轴的距离是
,到y轴的距离是
.
9.AB∥y轴,AB=3,若点A的坐标是(5,-4),则点B的坐标是
.
10.
如图,在平面直角坐标系中,点P的坐标为
.
11.
如图,P1、P2、P3这三个点中,在第二象限内的有
.
12.点P(a,b)满足ab>0,则点P在第
象限;点P(a,b)满足ab<0,则点P在第
象限;点P(a,b)满足ab=0,则点P在
.
13.已知点P的坐标为(3a-2,a+6),且点P到两坐标轴距离相等,则a=
.
14.
点(a+5,a-3)若在x轴上,则a的值为
,该点的坐标为
;若在y轴上,则a的值为
,该点的坐标为
.
15.
如图,在中国象棋的残局上建立平面直角坐标系,如果“相”和“兵”的坐标分别是(3,-1)和(-3,1),那么“卒”的坐标为
.
16.
如图所示,在平面直角坐标系中:
(1)描出下列各点:A(4,5)、B(-2,3)、C(-4,-1)、D(5,-2);
(2)写出平面直角坐标系中E、F、G、H、M、N点的坐标.
17.在直角坐标系内描出各点,并依次用线段连接各点:(4,4),(3,3),(4,3),(2,1),(4,1),(,0),(,0),(4,1),(6,1),(4,3),(5,3),(4,4).观察得到的图形,你觉得该图形像什么?求出所得到图形的面积.
18.已知点P(a-2,2a+8),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P在y轴上;
(3)点Q的坐标为(1,5),直线PQ∥y轴;
(4)点P到x轴、y轴的距离相等.
19.
某探险家得到一幅宝藏图,海岛上四棵古树的位置分别记作A(-1,-2)、B(4,3)、C(1,6)、D(5,-2),宝藏埋在直线AB和CD的交点处.
(1)在图中画出A、B、C、D四点;
(2)连接AB、CD,写出宝藏所在地的坐标.
20.
16.在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图所示.
(1)填写下列各点的坐标:A1(
,
)、A3(
,
)、A12(
,
);
(2)写出点A4n的坐标(n是正整数);
(3)写出蚂蚁从点A100到点A101的移动方向.
答案;
1-5
BADCB
6.
一
7.
三
8.
二
2
9.
(5,-1)或(5,-7)
10.
(3,-2)
11.
P1
12.
一、三
二、四
坐标轴上
13.
4或-1
14.
3
(8,0)
-5
(0,-8)
15.
(-2,-2)
16.
解:(1)图略;
(2)E(2,0)、F(0,-4)、G(-2,2)、H(1,-2)、M(4,1)、N(-3,-2).
17.
解:如图所示
:
该图形像宝塔松.
图形的面积为:×1×1+×4×2+×2×1=+4+1=.
18.
解:(1)P(-6,0); (2)P(0,12); (3)P(1,14); (4)P(-12,-12)或(-4,4).
19.
解:(1)描点如图所示:
(2)(3,2).
20.
解:(1)A1(0,1)、A3(1,0)、A12(6,0);
(2)A4n(2n,0);
(3)点A100中的100正好是4的倍数,所以点A100和A101的坐标分别是A100(50,0)、A101(50,1),所以蚂蚁从点A100到点A101的移动方向是从下向上.
