四川省成都市玉林中学2011-2012学年高二下学期期中考试数学(理)试题
文档属性
| 名称 | 四川省成都市玉林中学2011-2012学年高二下学期期中考试数学(理)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 202.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-27 13:41:27 | ||
图片预览


文档简介
一、选择题(本大题共12小题,每小题 5 分,共 60分).
1.若命题“”为假,且“”为假,则( )
A.或为假 B.假
C.真 D.不能判断的真假
2.从一个不透明的口袋中摸出红球的概率为,已知袋中红球有个,则袋中共有球的个数为( ).
A.个 B.个 C.个 D.个
3.为了判断甲、乙两名同学本学期几次数学考试成绩哪个稳定,通常需要知道这两个人的
( )
A.平均数 B.众数 C.方差 D.频率分布
4.过抛物线上一点的切线的倾斜角为( )
A. B. C. D.
5.同时掷两枚骰子,所得点数之和为的概率为( ).
A.1/4 B.1/9 C.1/6 D.1/12
6. 在一次歌手大奖赛上,七位评委为歌手打出的分数如下:
9.4
去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为 ( )
A. B. C. D.
7. 设,则是 的( )
A.充分但不必要条件 B. 必要但不充分条件
C.充要条件 D. 既不充分也不必要条件
8.若函数在内单调递减,则实数的范围为( )
A. B. C. D.
9. 已知条件,条件,则是的( )
A.充分不必要条件 B. 必要不充分条件
C.充要条件 D. 既不充分也不必要条件
10.( )
A. B. C. D.
11. 在腰长为的等腰直角三角形内任取一点,使得该点到此三角形的直角顶点的距离不大于的概率是( )
A. B. C. D.
12. 设、分别是定义在上的奇函数和偶函数,当时, >0,且. 则不等式的解集是 ( )
A. B.
C. D.
二、填空题(本大题共4小题,每小题 4 分,共 16分.把答案填在题中横线上)
13. 某工厂生产产品,用传送带将产品送至下一个工序,质检人员每隔十分钟在传送带某一位置取一件检验,则这种抽样的方法为 .
14. 过点且与曲线在点处的切线平行的直线方程是 .
15.盒子中装有形状、大小完全相同的个小球,其中红色球、黄色球各个,若从中随机抽取个球,则所取出的个球颜色不同的概率等于
16.有下列四个结论:
①命题“若,则,互为倒数”的逆命题;
②命题“面积相等的三角形不全等”的否命题;
③命题“若,则有实根”的逆否命题;
④命题, 的否定是:,
其中结论正确或是真命题的是 (填上你认为正确的结论序号)。
三、解答题(本大题共6小题,共 74分).
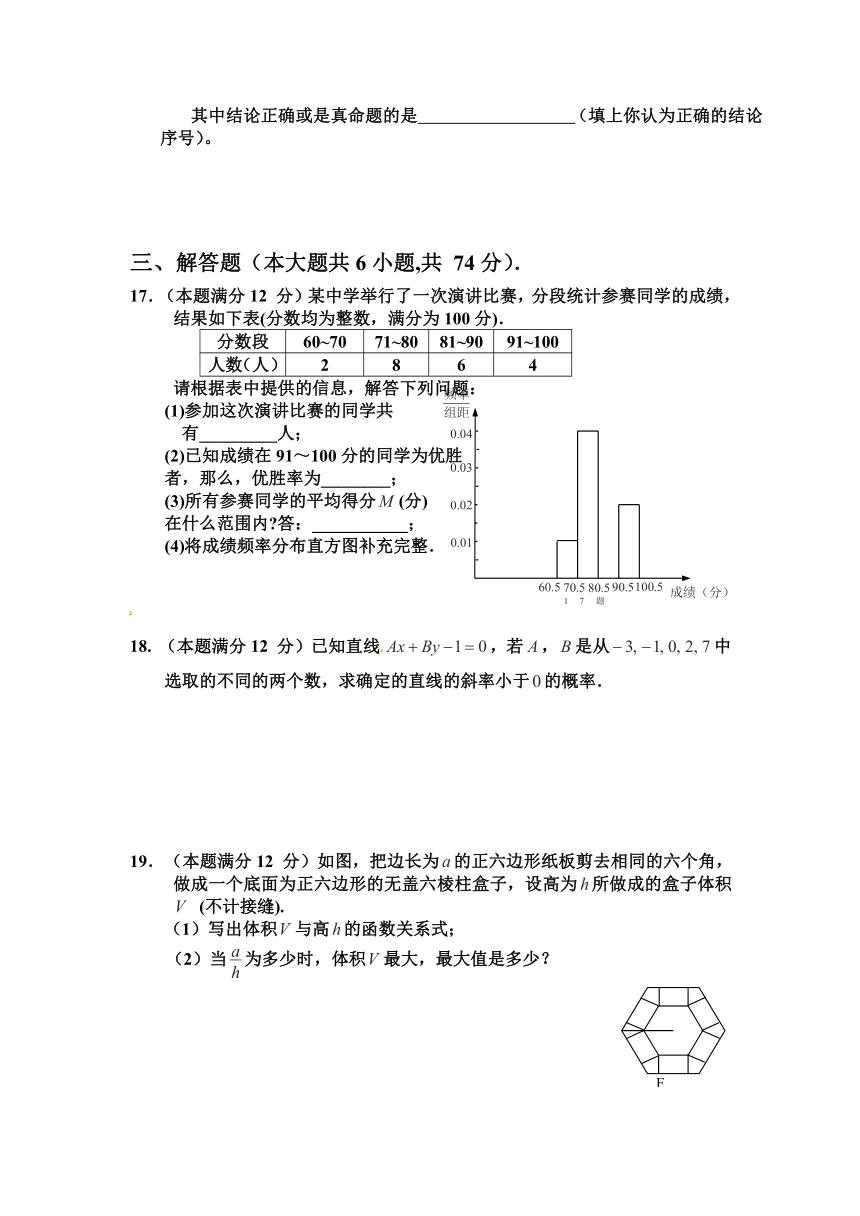
17.(本题满分12 分)某中学举行了一次演讲比赛,分段统计参赛同学的成绩,结果如下表(分数均为整数,满分为100分).
分数段 60~70 71~80 81~90 91~100
人数(人) 2 8 6 4
请根据表中提供的信息,解答下列问题:
(1)参加这次演讲比赛的同学共
有_________人;
(2)已知成绩在91~100分的同学为优胜
者,那么,优胜率为________;
(3)所有参赛同学的平均得分(分)
在什么范围内 答:___________;
(4)将成绩频率分布直方图补充完整.
18. (本题满分12 分)已知直线,若,是从中选取的不同的两个数,求确定的直线的斜率小于的概率.
19.(本题满分12 分)如图,把边长为的正六边形纸板剪去相同的六个角,做成一个底面为正六边形的无盖六棱柱盒子,设高为所做成的盒子体积 (不计接缝).
(1)写出体积与高的函数关系式;
(2)当为多少时,体积最大,最大值是多少?
20.(本题满分12 分)设,,
(1)求的单调区间
(2)若在方程与方程中,至少有一个方程有实数根,求实数的取值范围。
21. (本题满分12 分)(1)在区间上任取一数,求这个数大于的概率
(2)在区间中随机地取出两个数,求这两个数的和小于的概率。
22. (本题满分14 分)已知过函数f(x)=的图象上一点的切线的斜率为
(1)求、的值;
(2)求的取值范围,使不等式f(x)对于恒成立;
(3)令,是否存在一个实数,使得当时, 有最大值?
参考解答:
20.解:定义域为(0,+∞),
22.解:(1)=
列表如下:
x (0, )
+ 0 -
g(x) ↗ 极大值 ↘
g(x)在x=处取最大值-+t=1
∴t==<3
∴x=<1
③当t<0时,<0,∴g(x)在上为减函数,
∴g(x)在上为增函数,
∴存在一个a=,使g(x)在上有最大值1。
F
B C
1.若命题“”为假,且“”为假,则( )
A.或为假 B.假
C.真 D.不能判断的真假
2.从一个不透明的口袋中摸出红球的概率为,已知袋中红球有个,则袋中共有球的个数为( ).
A.个 B.个 C.个 D.个
3.为了判断甲、乙两名同学本学期几次数学考试成绩哪个稳定,通常需要知道这两个人的
( )
A.平均数 B.众数 C.方差 D.频率分布
4.过抛物线上一点的切线的倾斜角为( )
A. B. C. D.
5.同时掷两枚骰子,所得点数之和为的概率为( ).
A.1/4 B.1/9 C.1/6 D.1/12
6. 在一次歌手大奖赛上,七位评委为歌手打出的分数如下:
9.4
去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为 ( )
A. B. C. D.
7. 设,则是 的( )
A.充分但不必要条件 B. 必要但不充分条件
C.充要条件 D. 既不充分也不必要条件
8.若函数在内单调递减,则实数的范围为( )
A. B. C. D.
9. 已知条件,条件,则是的( )
A.充分不必要条件 B. 必要不充分条件
C.充要条件 D. 既不充分也不必要条件
10.( )
A. B. C. D.
11. 在腰长为的等腰直角三角形内任取一点,使得该点到此三角形的直角顶点的距离不大于的概率是( )
A. B. C. D.
12. 设、分别是定义在上的奇函数和偶函数,当时, >0,且. 则不等式的解集是 ( )
A. B.
C. D.
二、填空题(本大题共4小题,每小题 4 分,共 16分.把答案填在题中横线上)
13. 某工厂生产产品,用传送带将产品送至下一个工序,质检人员每隔十分钟在传送带某一位置取一件检验,则这种抽样的方法为 .
14. 过点且与曲线在点处的切线平行的直线方程是 .
15.盒子中装有形状、大小完全相同的个小球,其中红色球、黄色球各个,若从中随机抽取个球,则所取出的个球颜色不同的概率等于
16.有下列四个结论:
①命题“若,则,互为倒数”的逆命题;
②命题“面积相等的三角形不全等”的否命题;
③命题“若,则有实根”的逆否命题;
④命题, 的否定是:,
其中结论正确或是真命题的是 (填上你认为正确的结论序号)。
三、解答题(本大题共6小题,共 74分).
17.(本题满分12 分)某中学举行了一次演讲比赛,分段统计参赛同学的成绩,结果如下表(分数均为整数,满分为100分).
分数段 60~70 71~80 81~90 91~100
人数(人) 2 8 6 4
请根据表中提供的信息,解答下列问题:
(1)参加这次演讲比赛的同学共
有_________人;
(2)已知成绩在91~100分的同学为优胜
者,那么,优胜率为________;
(3)所有参赛同学的平均得分(分)
在什么范围内 答:___________;
(4)将成绩频率分布直方图补充完整.
18. (本题满分12 分)已知直线,若,是从中选取的不同的两个数,求确定的直线的斜率小于的概率.
19.(本题满分12 分)如图,把边长为的正六边形纸板剪去相同的六个角,做成一个底面为正六边形的无盖六棱柱盒子,设高为所做成的盒子体积 (不计接缝).
(1)写出体积与高的函数关系式;
(2)当为多少时,体积最大,最大值是多少?
20.(本题满分12 分)设,,
(1)求的单调区间
(2)若在方程与方程中,至少有一个方程有实数根,求实数的取值范围。
21. (本题满分12 分)(1)在区间上任取一数,求这个数大于的概率
(2)在区间中随机地取出两个数,求这两个数的和小于的概率。
22. (本题满分14 分)已知过函数f(x)=的图象上一点的切线的斜率为
(1)求、的值;
(2)求的取值范围,使不等式f(x)对于恒成立;
(3)令,是否存在一个实数,使得当时, 有最大值?
参考解答:
20.解:定义域为(0,+∞),
22.解:(1)=
列表如下:
x (0, )
+ 0 -
g(x) ↗ 极大值 ↘
g(x)在x=处取最大值-+t=1
∴t==<3
∴x=<1
③当t<0时,<0,∴g(x)在上为减函数,
∴g(x)在上为增函数,
∴存在一个a=,使g(x)在上有最大值1。
F
B C
同课章节目录
