11.2.2 三角形的外角 训练 2021-2022学年人教版数学八年级上册(Word版含答案)
文档属性
| 名称 | 11.2.2 三角形的外角 训练 2021-2022学年人教版数学八年级上册(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 118.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-08 11:38:29 | ||
图片预览



文档简介
11.2.2
三角形的外角
课堂笔记
1.由三角形的内角和定理可以得到以下常用的结论:
任何三角形中,至少有个锐角,至多有个锐角;最多有
个钝角;最多有个直角.
2.
三角形的外角性质
三角形的外角等于
.
三角形的外角大于.
训练
1.
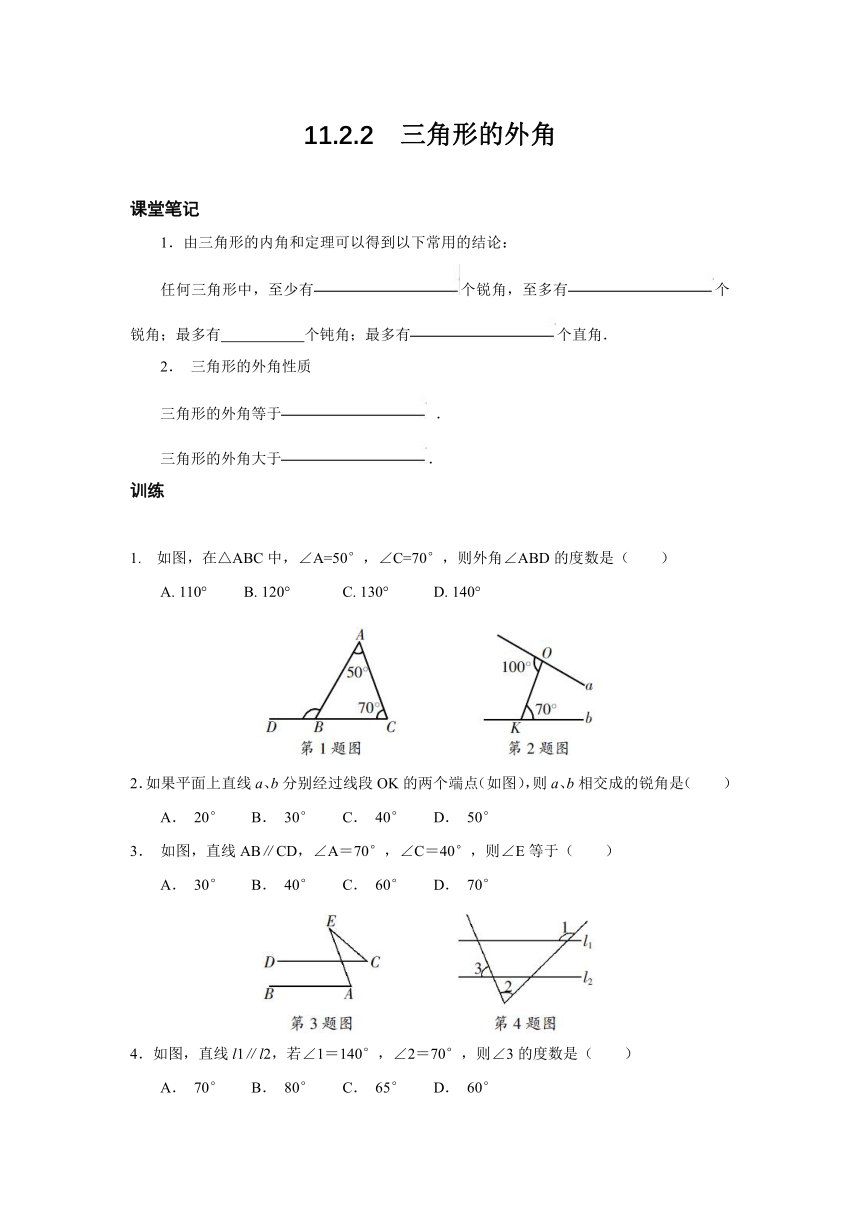
如图,在△ABC中,∠A=50°,∠C=70°,则外角∠ABD的度数是(
)
A.
110°
B.
120°
C.
130°
D.
140°
2.如果平面上直线a、b分别经过线段OK的两个端点(如图),则a、b相交成的锐角是(
)
A.
20°
B.
30°
C.
40°
D.
50°
3.
如图,直线AB∥CD,∠A=70°,∠C=40°,则∠E等于(
)
A.
30°
B.
40°
C.
60°
D.
70°
4.如图,直线l1∥l2,若∠1=140°,∠2=70°,则∠3的度数是(
)
A.
70°
B.
80°
C.
65°
D.
60°
5.一副三角板有两个直角三角形,如图叠放在一起,则∠α的度数是(
)
A.
165°
B.
120°
C.
150°
D.
135°
6.
△ABC中,若∠C-∠B=∠A,则△ABC的外角中最小的角是(填“锐角”、“直角”或“钝角”).
7.
如图,△ABC中,点D在BC的延长线上,点F是AB边上一点,延长CA到E,连接EF,则∠1,∠2,∠3的大小关系是.
8.
如图所示,∠1=
.
9.
如图,D是AB上一点,E是AC上一点,BE、CD相交于点F,∠A=62°,∠ACD=35°,∠ABE=20°,求∠BDC和∠BFD的度数.
10.
如图是一副三角板拼成的图案,则∠AEB=
度.
11.
如图,D,E,F分别是△ABC三边延长线上的点,连接AE,BF,CD,则∠D+∠E+∠F+∠1+∠2+∠3=
.
12.
如图,在△ABC中,∠B=47°,三角形的外角∠DAC和∠ACF的平分线交于点E,求∠AEC的度数.
13.
如图,在△ABC中,BA1平分∠ABC,CA1平分∠ACD,BA1、CA1相交于点A1.
(1)求证:∠A1=∠A;
(2)如图,继续作∠A1BC和∠A1CD的平分线交于点A2得∠A2,作∠A2BC和∠A2CD的平分线交于点A3得∠A3,…,作∠A2019BC和∠A2019CD的平分线交于A2020得∠A2020,若∠A=α,则∠A2020=
(用含α的式子表示).
14.平面内的两条直线有相交和平行两种位置关系:
(1)如图a,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B-∠D.
将点P移到AB、CD内部,如图b,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;
(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系?(不需证明)
(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.
参考答案
【课堂笔记】
1.
2
3
1
1
2.
与它不相邻的两个内角的和
和它不相邻的任意一个内角
【训练】
1—5.
BBAAA
6.
直角
7.
∠1>∠2>∠3
8.
120°
9.
∠BDC=97°
∠BFD=63°
10.
75
11.
180°
12.
∵三角形的外角∠DAC和∠ACF的平分线交于点E,
∴∠EAC=∠DAC,∠ECA=∠ACF;
又∵∠B=47°(已知),∠B+∠1+∠2=180°(三角形内角和定理),
∴∠DAC+∠ACF=(∠B+∠2)+(∠B+∠1)=(∠B+∠B+∠1+∠2)=
(外角定理),
∴∠AEC=180°-(∠DAC+∠ACF)=66.5°.
13.
(1)∵CA1平分∠ACD,∴∠A1CD=∠ACD=(∠A+∠ABC),
又∵∠A1CD=∠A1+∠A1BC,∴∠A1+∠A1BC=(∠A+∠ABC),
∵BA1平分∠ABC,∴∠A1BC=∠ABC,
∴∠ABC+∠A1=(∠A+∠ABC),∴∠A1=∠A.
(2)
14.
(1)不成立,结论是∠BPD=∠B+∠D.
证明:延长BP交CD于点E,
∵AB∥CD,∴∠B=∠BED,
又∵∠BPD=∠BED+∠D,∴∠BPD=∠B+∠D.
(2)∠BPD=∠B+∠D+∠BQD.
(3)连接EG并延长,由三角形的外角性质得∠AGB=∠A+∠B+∠AEB,
又∵∠AGB=∠CGF,在四边形CDFG中,∠CGF+∠C+∠D+∠F=360°,
∴∠A+∠B+∠C+∠D+∠AEB+∠F=360°.
三角形的外角
课堂笔记
1.由三角形的内角和定理可以得到以下常用的结论:
任何三角形中,至少有个锐角,至多有个锐角;最多有
个钝角;最多有个直角.
2.
三角形的外角性质
三角形的外角等于
.
三角形的外角大于.
训练
1.
如图,在△ABC中,∠A=50°,∠C=70°,则外角∠ABD的度数是(
)
A.
110°
B.
120°
C.
130°
D.
140°
2.如果平面上直线a、b分别经过线段OK的两个端点(如图),则a、b相交成的锐角是(
)
A.
20°
B.
30°
C.
40°
D.
50°
3.
如图,直线AB∥CD,∠A=70°,∠C=40°,则∠E等于(
)
A.
30°
B.
40°
C.
60°
D.
70°
4.如图,直线l1∥l2,若∠1=140°,∠2=70°,则∠3的度数是(
)
A.
70°
B.
80°
C.
65°
D.
60°
5.一副三角板有两个直角三角形,如图叠放在一起,则∠α的度数是(
)
A.
165°
B.
120°
C.
150°
D.
135°
6.
△ABC中,若∠C-∠B=∠A,则△ABC的外角中最小的角是(填“锐角”、“直角”或“钝角”).
7.
如图,△ABC中,点D在BC的延长线上,点F是AB边上一点,延长CA到E,连接EF,则∠1,∠2,∠3的大小关系是.
8.
如图所示,∠1=
.
9.
如图,D是AB上一点,E是AC上一点,BE、CD相交于点F,∠A=62°,∠ACD=35°,∠ABE=20°,求∠BDC和∠BFD的度数.
10.
如图是一副三角板拼成的图案,则∠AEB=
度.
11.
如图,D,E,F分别是△ABC三边延长线上的点,连接AE,BF,CD,则∠D+∠E+∠F+∠1+∠2+∠3=
.
12.
如图,在△ABC中,∠B=47°,三角形的外角∠DAC和∠ACF的平分线交于点E,求∠AEC的度数.
13.
如图,在△ABC中,BA1平分∠ABC,CA1平分∠ACD,BA1、CA1相交于点A1.
(1)求证:∠A1=∠A;
(2)如图,继续作∠A1BC和∠A1CD的平分线交于点A2得∠A2,作∠A2BC和∠A2CD的平分线交于点A3得∠A3,…,作∠A2019BC和∠A2019CD的平分线交于A2020得∠A2020,若∠A=α,则∠A2020=
(用含α的式子表示).
14.平面内的两条直线有相交和平行两种位置关系:
(1)如图a,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B-∠D.
将点P移到AB、CD内部,如图b,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;
(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系?(不需证明)
(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.
参考答案
【课堂笔记】
1.
2
3
1
1
2.
与它不相邻的两个内角的和
和它不相邻的任意一个内角
【训练】
1—5.
BBAAA
6.
直角
7.
∠1>∠2>∠3
8.
120°
9.
∠BDC=97°
∠BFD=63°
10.
75
11.
180°
12.
∵三角形的外角∠DAC和∠ACF的平分线交于点E,
∴∠EAC=∠DAC,∠ECA=∠ACF;
又∵∠B=47°(已知),∠B+∠1+∠2=180°(三角形内角和定理),
∴∠DAC+∠ACF=(∠B+∠2)+(∠B+∠1)=(∠B+∠B+∠1+∠2)=
(外角定理),
∴∠AEC=180°-(∠DAC+∠ACF)=66.5°.
13.
(1)∵CA1平分∠ACD,∴∠A1CD=∠ACD=(∠A+∠ABC),
又∵∠A1CD=∠A1+∠A1BC,∴∠A1+∠A1BC=(∠A+∠ABC),
∵BA1平分∠ABC,∴∠A1BC=∠ABC,
∴∠ABC+∠A1=(∠A+∠ABC),∴∠A1=∠A.
(2)
14.
(1)不成立,结论是∠BPD=∠B+∠D.
证明:延长BP交CD于点E,
∵AB∥CD,∴∠B=∠BED,
又∵∠BPD=∠BED+∠D,∴∠BPD=∠B+∠D.
(2)∠BPD=∠B+∠D+∠BQD.
(3)连接EG并延长,由三角形的外角性质得∠AGB=∠A+∠B+∠AEB,
又∵∠AGB=∠CGF,在四边形CDFG中,∠CGF+∠C+∠D+∠F=360°,
∴∠A+∠B+∠C+∠D+∠AEB+∠F=360°.
