3.1.2 等式的性质 同步课件 2021-2022学年人教版数学七年级上册(共17张ppt)
文档属性
| 名称 | 3.1.2 等式的性质 同步课件 2021-2022学年人教版数学七年级上册(共17张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 162.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-08 08:53:46 | ||
图片预览





文档简介
第三章 一元一次方程
3.1.2 等式的性质
知识回顾
(1)什么叫做方程?
(2)什么叫做一元一次方程?
(3)一元一次方程有哪几个特征?
①只含有一个未知数;
②未知数的次数都是1;
③整式方程.
含有未知数的等式
含有一个未知数,且未知数的次数是1
(4)什么是方程的解?
使方程等号两边相等的未知数的值
获取新知
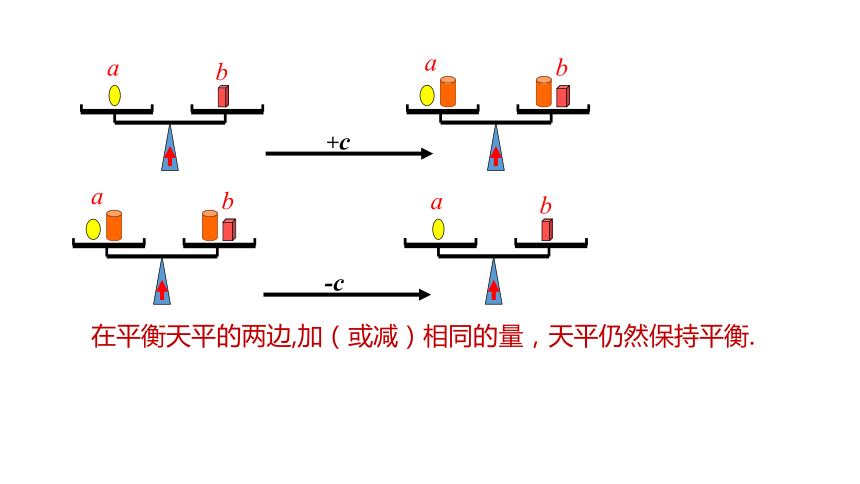
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等号成立就可看作是天平保持两边平衡.
通常可以用a=b表示一般的等式.
在平衡天平的两边,加(或减)相同的量,天平仍然保持平衡.
+c
a
b
a
b
a
b
-c
a
b
等式的性质1 等式两边加(或减)同一数(或式子),结果仍相等.
如果a=b,那么a±c = b±c.
字母a、b、c可以表示具体的数,也可以表示一个式子
×3
÷ 3
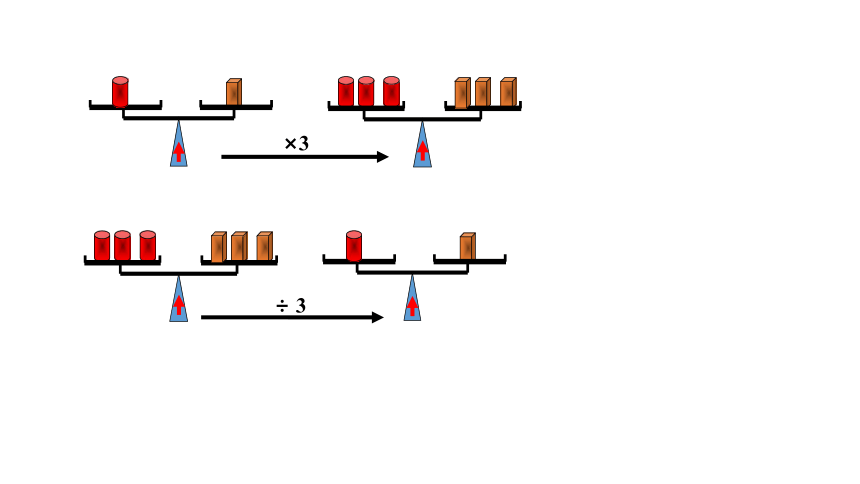
等式的性质2 等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
如果a=b, 那么ac=bc;
如果a=b(c≠0), 那么 .
例题讲解
(2) 怎样从等式 3+x=1 得到等式 x =-2?
(3) 怎样从等式 4x=12 得到等式 x =3?
依据等式的性质1两边同时减3.
依据等式的性质2两边同时除以4或同乘 .
依据等式的性质2两边同时除以 或同乘100.
例1 (1) 怎样从等式 x-5= y-5 得到等式 x = y ?
依据等式的性质1两边同时加5.
(4) 怎样从等式 得到等式 a = b?
例2 利用等式的性质解下列方程:
(1) x+7 = 26; (2) -5x=20; (3) -5=4.
分析:要使方程x+7 = 26转化为x=a (常数)的形式, 需去掉方程左边的7,利用等式的性质1,方程两边减7就得出x的值.你可以类似地考虑另两个方程如何转化为x=a的形式.
解:(1)两边减7,得x+7-7=26-7.
于是x=19.
解以x为未知数的方程,就是把方程逐步转化为x= a (常 数)的形式,等式的性质是转化的重要依据.
例2 利用等式的性质解下列方程:
(1) x+7 = 26; (2) -5x=20; (3) -5=4.
(2)两边除以-5,得
? 于是x= - 4.
解以x为未知数的方程,就是把方程逐步转化为x= a (常 数)的形式,等式的性质是转化的重要依据.
例2 利用等式的性质解下列方程:
(1) x+7 = 26; (2) -5x=20; (3) -5=4.
(3)两边加5,得
解以x为未知数的方程,就是把方程逐步转化为x= a (常 数)的形式,等式的性质是转化的重要依据.
例2 利用等式的性质解下列方程:
(1) x+7 = 26; (2) -5x=20; (3) -5=4.
随堂演练
1. 下列各种变形中,不正确的是( )
A.由2+x=5可得到x=5-2
B.由3x=2x-1可得到3x-2x=-1
C.由5x=4x+1可得到4x-5x=1
D.由6x-2x=-3可得到6x=2x-3
C
2. 下列变形,正确的是( )
A.如果a=b,那么
B.如果 ,那么a=b
C.如果a2=3a,那么a=3
D.如果 -1=x,那么2x+1-1=3x
B
4. 填空
(1) 将等式x-3=5 的两边都_____得到x =8 ,这是
根据等式的性质__;
(2) 将等式 的两边都乘以___或除以 ___得
到 x = -2,这是根据等式性质 ___;
加3
1
2
2
5. 利用等式的性质解下列方程:
(1)8+x=-5; (2) y=6;
(3)-3x+7=1; (4)3x=2x+12.
解:(1)两边减8,
得8+x-8=-5-8.
于是x=-13.
(2)两边乘-5,
得y=-30.
(3)两边减7,
得-3x+7-7=1-7.
化简,得-3x=-6.
两边除以-3,得x=2.
(4)两边减2x,得x=12.
课堂小结
等式的
基本性质
基本性质1
基本性质2
应用
如果a=b,那么a±c=b±c.
运用等式的性质把方程
“化归”为最简的形式 x = a
如果a=b,那么ac=bc;
如果a=b(c≠0),那么 .
3.1.2 等式的性质
知识回顾
(1)什么叫做方程?
(2)什么叫做一元一次方程?
(3)一元一次方程有哪几个特征?
①只含有一个未知数;
②未知数的次数都是1;
③整式方程.
含有未知数的等式
含有一个未知数,且未知数的次数是1
(4)什么是方程的解?
使方程等号两边相等的未知数的值
获取新知
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等号成立就可看作是天平保持两边平衡.
通常可以用a=b表示一般的等式.
在平衡天平的两边,加(或减)相同的量,天平仍然保持平衡.
+c
a
b
a
b
a
b
-c
a
b
等式的性质1 等式两边加(或减)同一数(或式子),结果仍相等.
如果a=b,那么a±c = b±c.
字母a、b、c可以表示具体的数,也可以表示一个式子
×3
÷ 3
等式的性质2 等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
如果a=b, 那么ac=bc;
如果a=b(c≠0), 那么 .
例题讲解
(2) 怎样从等式 3+x=1 得到等式 x =-2?
(3) 怎样从等式 4x=12 得到等式 x =3?
依据等式的性质1两边同时减3.
依据等式的性质2两边同时除以4或同乘 .
依据等式的性质2两边同时除以 或同乘100.
例1 (1) 怎样从等式 x-5= y-5 得到等式 x = y ?
依据等式的性质1两边同时加5.
(4) 怎样从等式 得到等式 a = b?
例2 利用等式的性质解下列方程:
(1) x+7 = 26; (2) -5x=20; (3) -5=4.
分析:要使方程x+7 = 26转化为x=a (常数)的形式, 需去掉方程左边的7,利用等式的性质1,方程两边减7就得出x的值.你可以类似地考虑另两个方程如何转化为x=a的形式.
解:(1)两边减7,得x+7-7=26-7.
于是x=19.
解以x为未知数的方程,就是把方程逐步转化为x= a (常 数)的形式,等式的性质是转化的重要依据.
例2 利用等式的性质解下列方程:
(1) x+7 = 26; (2) -5x=20; (3) -5=4.
(2)两边除以-5,得
? 于是x= - 4.
解以x为未知数的方程,就是把方程逐步转化为x= a (常 数)的形式,等式的性质是转化的重要依据.
例2 利用等式的性质解下列方程:
(1) x+7 = 26; (2) -5x=20; (3) -5=4.
(3)两边加5,得
解以x为未知数的方程,就是把方程逐步转化为x= a (常 数)的形式,等式的性质是转化的重要依据.
例2 利用等式的性质解下列方程:
(1) x+7 = 26; (2) -5x=20; (3) -5=4.
随堂演练
1. 下列各种变形中,不正确的是( )
A.由2+x=5可得到x=5-2
B.由3x=2x-1可得到3x-2x=-1
C.由5x=4x+1可得到4x-5x=1
D.由6x-2x=-3可得到6x=2x-3
C
2. 下列变形,正确的是( )
A.如果a=b,那么
B.如果 ,那么a=b
C.如果a2=3a,那么a=3
D.如果 -1=x,那么2x+1-1=3x
B
4. 填空
(1) 将等式x-3=5 的两边都_____得到x =8 ,这是
根据等式的性质__;
(2) 将等式 的两边都乘以___或除以 ___得
到 x = -2,这是根据等式性质 ___;
加3
1
2
2
5. 利用等式的性质解下列方程:
(1)8+x=-5; (2) y=6;
(3)-3x+7=1; (4)3x=2x+12.
解:(1)两边减8,
得8+x-8=-5-8.
于是x=-13.
(2)两边乘-5,
得y=-30.
(3)两边减7,
得-3x+7-7=1-7.
化简,得-3x=-6.
两边除以-3,得x=2.
(4)两边减2x,得x=12.
课堂小结
等式的
基本性质
基本性质1
基本性质2
应用
如果a=b,那么a±c=b±c.
运用等式的性质把方程
“化归”为最简的形式 x = a
如果a=b,那么ac=bc;
如果a=b(c≠0),那么 .
