11.1 三角形的边 课件 2021--2022学年八年级数学人教版上册(共19张ppt)
文档属性
| 名称 | 11.1 三角形的边 课件 2021--2022学年八年级数学人教版上册(共19张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 111.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-08 00:00:00 | ||
图片预览






文档简介
第十一章 三角形
第1课时 三角形的边
三角形的定义:由不在同1条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.组成三角形的线段叫做三角形的边;相邻两边的公共端点叫做三角形的顶点;相邻两边组成的角叫做三角形的内角,简称三角形的角.
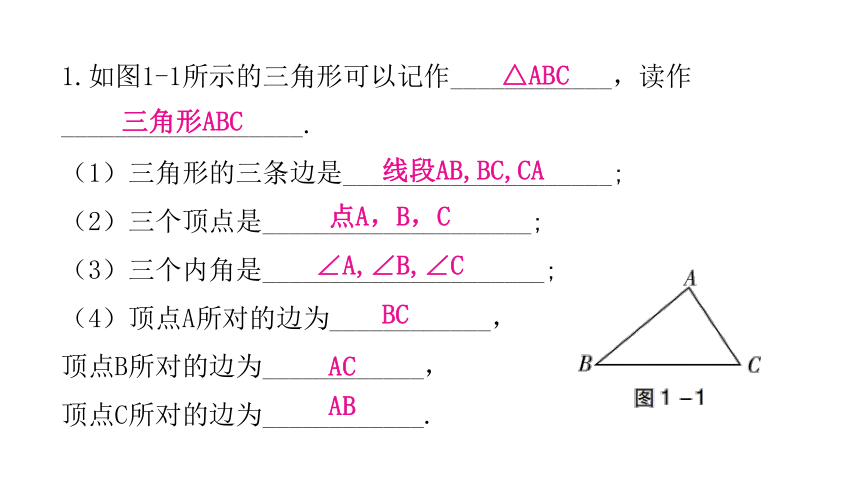
1.如图1-1所示的三角形可以记作____________,读作__________________.
(1)三角形的三条边是____________________;
(2)三个顶点是____________________;
(3)三个内角是_____________________;
(4)顶点A所对的边为____________,
顶点B所对的边为____________,
顶点C所对的边为____________.
△ABC
三角形ABC
线段AB,BC,CA
点A,B,C
∠A,∠B,∠C
BC
AC
AB
不能
2. 长度为2,3,5的三条线段,能否组成三角形?___________(填“能”或“不能”).
3. 给出下列说法:①等边三角形是等腰三角形;②三角形按边的相等关系分类可分为等腰三角形、等边三角形和不等边三角形;③三角形按角的大小分类可分为锐角三角形、直角三角形和钝角三角形.其中,正确的是_________________.
①③
【例1】以下列长度的线段为边,可以作一个三角形的是
( )
A.1 cm,1 cm,2 cm
B.3 cm,4 cm,5 cm
C.1 cm,4 cm,6 cm
D.2 cm,3 cm,7 cm
典型例题
知识点1 三角形的三边关系——判断能否构成三角形
B
1. 下列长度(单位:cm)的三条线段,不能围成三角形的是 ( )
A.3,8,4 B.9,15,8
C.15,20,8 D.6,4,9
变式训练
A
【例2】(1)一个三角形的两边分别为4 cm和8 cm,则第三边的长x的取值范围是____________________________;
(2)已知三角形的三边长分别为1,x,5,且x为整数,则x=____________.
典型例题
知识点2 三角形的三边关系——求第三边的取值范围
4 cm<x<12 cm
5
2. (1)设三角形三边的长分别为2,9,5+a,则a的取值范围为____________________;
(2)△ABC两边的长分别是2和5,且第三边的长为奇数,则第三边的长为____________.
变式训练
2<a<6
5
【例3】用一条长为20 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么该等腰三角形各边的长分别是多少?
(2)能围成有一边的长是4 cm的等腰三角形吗?为什么?
典型例题
知识点3 有关等腰三角形的计算
3. 用一条长为35 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的3倍,那么该等腰三角形各边的长分别是多少?
(2)通过计算说明能否围成有一边的长为1 cm的等腰三角形.
变式训练
4. 下列各组数可作为一个三角形三边长的是 ( )
A.4,6,8 B.4,5,9
C.1,2,4 D.5,5,11
5. 如果线段a,b,c能组成三角形,那么它们的长度比可能是 ( )
A.1∶2∶4 B.2∶3∶4
C.3∶4∶7 D.1∶3∶4
A
B
6. 在△ABC中,AB=4,BC=10,则第三边AC的长可能是
( )
A.5 B.7
C.14 D.16
7. 已知线段a=5,b=3,线段c与a,b构成三角形,则线段c的长度的取值范围是 ( )
A.c>2 B.c<8
C.2<c<8 D.无法确定
B
C
8. 已知三角形的三边长分别为2,x,10,若x为正整数,则这样的三角形个数为 ( )
A.1 B.2 C.3 D.4
9. 填空:
(1)已知一个等腰三角形有一边的长为5,一边的长为2,则其周长为____________;
(2)一个等腰三角形一边的长等于6,一边的长等于5,则它的周长为____________.
C
12
16或17
10. 在△ABC中,已知AB=3,AC=7,若第三边BC的长为偶数,求△ABC的周长.
11. 有一条长为21 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的3倍,那么底边长是多少?
(2)通过计算说明能否围成一边长为5 cm的等腰三角形.请说明理由.
12. 观察如图1-2的图形,进行填空.
(1)图1-2②有____________个三角形,图1-2③有____________个三角形,图④有____________个三角形,…,猜测图1-2⑦有____________个三角形;
(2)按上面的方法继续下去,第n个图形中有____________个三角形.(用含n的式子填空)
3
5
7
13
(2n-1)
13. 如图1-3,已知点P是△ABC内一点,试证明PA+PB+PC>12(AB+BC+AC).
?
谢 谢
第1课时 三角形的边
三角形的定义:由不在同1条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.组成三角形的线段叫做三角形的边;相邻两边的公共端点叫做三角形的顶点;相邻两边组成的角叫做三角形的内角,简称三角形的角.
1.如图1-1所示的三角形可以记作____________,读作__________________.
(1)三角形的三条边是____________________;
(2)三个顶点是____________________;
(3)三个内角是_____________________;
(4)顶点A所对的边为____________,
顶点B所对的边为____________,
顶点C所对的边为____________.
△ABC
三角形ABC
线段AB,BC,CA
点A,B,C
∠A,∠B,∠C
BC
AC
AB
不能
2. 长度为2,3,5的三条线段,能否组成三角形?___________(填“能”或“不能”).
3. 给出下列说法:①等边三角形是等腰三角形;②三角形按边的相等关系分类可分为等腰三角形、等边三角形和不等边三角形;③三角形按角的大小分类可分为锐角三角形、直角三角形和钝角三角形.其中,正确的是_________________.
①③
【例1】以下列长度的线段为边,可以作一个三角形的是
( )
A.1 cm,1 cm,2 cm
B.3 cm,4 cm,5 cm
C.1 cm,4 cm,6 cm
D.2 cm,3 cm,7 cm
典型例题
知识点1 三角形的三边关系——判断能否构成三角形
B
1. 下列长度(单位:cm)的三条线段,不能围成三角形的是 ( )
A.3,8,4 B.9,15,8
C.15,20,8 D.6,4,9
变式训练
A
【例2】(1)一个三角形的两边分别为4 cm和8 cm,则第三边的长x的取值范围是____________________________;
(2)已知三角形的三边长分别为1,x,5,且x为整数,则x=____________.
典型例题
知识点2 三角形的三边关系——求第三边的取值范围
4 cm<x<12 cm
5
2. (1)设三角形三边的长分别为2,9,5+a,则a的取值范围为____________________;
(2)△ABC两边的长分别是2和5,且第三边的长为奇数,则第三边的长为____________.
变式训练
2<a<6
5
【例3】用一条长为20 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么该等腰三角形各边的长分别是多少?
(2)能围成有一边的长是4 cm的等腰三角形吗?为什么?
典型例题
知识点3 有关等腰三角形的计算
3. 用一条长为35 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的3倍,那么该等腰三角形各边的长分别是多少?
(2)通过计算说明能否围成有一边的长为1 cm的等腰三角形.
变式训练
4. 下列各组数可作为一个三角形三边长的是 ( )
A.4,6,8 B.4,5,9
C.1,2,4 D.5,5,11
5. 如果线段a,b,c能组成三角形,那么它们的长度比可能是 ( )
A.1∶2∶4 B.2∶3∶4
C.3∶4∶7 D.1∶3∶4
A
B
6. 在△ABC中,AB=4,BC=10,则第三边AC的长可能是
( )
A.5 B.7
C.14 D.16
7. 已知线段a=5,b=3,线段c与a,b构成三角形,则线段c的长度的取值范围是 ( )
A.c>2 B.c<8
C.2<c<8 D.无法确定
B
C
8. 已知三角形的三边长分别为2,x,10,若x为正整数,则这样的三角形个数为 ( )
A.1 B.2 C.3 D.4
9. 填空:
(1)已知一个等腰三角形有一边的长为5,一边的长为2,则其周长为____________;
(2)一个等腰三角形一边的长等于6,一边的长等于5,则它的周长为____________.
C
12
16或17
10. 在△ABC中,已知AB=3,AC=7,若第三边BC的长为偶数,求△ABC的周长.
11. 有一条长为21 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的3倍,那么底边长是多少?
(2)通过计算说明能否围成一边长为5 cm的等腰三角形.请说明理由.
12. 观察如图1-2的图形,进行填空.
(1)图1-2②有____________个三角形,图1-2③有____________个三角形,图④有____________个三角形,…,猜测图1-2⑦有____________个三角形;
(2)按上面的方法继续下去,第n个图形中有____________个三角形.(用含n的式子填空)
3
5
7
13
(2n-1)
13. 如图1-3,已知点P是△ABC内一点,试证明PA+PB+PC>12(AB+BC+AC).
?
谢 谢
