5.1.4 用样本估计总体(第2课时)教案-2021-2022学年高一上学期数学人教B版(2019)必修第二册
文档属性
| 名称 | 5.1.4 用样本估计总体(第2课时)教案-2021-2022学年高一上学期数学人教B版(2019)必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 115.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-09 09:17:14 | ||
图片预览


文档简介
5.1.4
用样本估计总体
第二课时
教案
教学课时:第2课时
教学目标:
通过具体实例,学生体会样本与总体的关系,体验用样本的分布估计总体的分布.
教学重点:
样本的分布估计总体的分布.
教学难点:
用样本“估计总体”,?突出“用局部估计总体”的思想.
教学过程:
前面一节课,我们体会了可以用样本的数字特征估计总体的数字特征,那么,总体的分布是否也可以用样本的分布来近似刻画呢?
一、【尝试与发现】(课本80页)
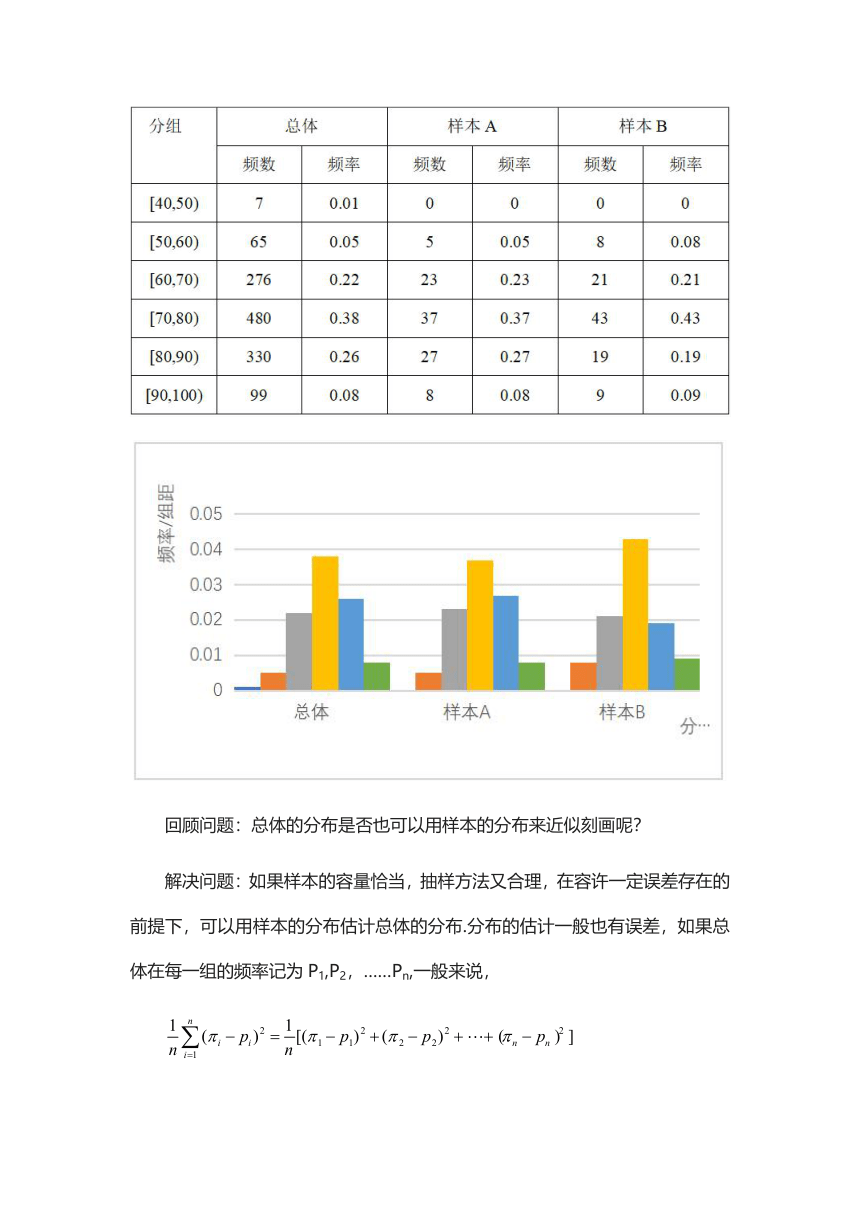
通过对某中学1257名高一学生期中考试的数学成绩(具体数据参见课本85-87页)进行整理,可以得到如下数据,并由此可作出频率分布直方图和折线图,如图所示.
【学生活动1】
在附录的数据中抽取容量是100的样本,整理类似的表格,并制作频率分布直方图.
学生分成2组,选用随机抽样的方法分别抽取容量是100的样本,分别记为样本A,样本B?,分别得到如下的频数、频率对应表,它们的频率分布直方图,借助信息技术完成相应任务.
【设计意图】
这个活动意在让学生体会和感受统计的思想方法,学生经历和体验了数据收集、数据处理等过程,真正理解统计的思想方法.
回顾问题:总体的分布是否也可以用样本的分布来近似刻画呢?
解决问题:如果样本的容量恰当,抽样方法又合理,在容许一定误差存在的前提下,可以用样本的分布估计总体的分布.分布的估计一般也有误差,如果总体在每一组的频率记为P1,P2,……Pn,一般来说,
不等于零,同样,大数定律可以保证,当样本的容量越来越大时,上式很小的可能性将越来越大.
二、“大数据”简介
学生自行完成课本83页“大数据”阅读,对“大数据”价值的认识,有利于学生对未来职业的选择、个人发展规划的制定,激发学生学习的兴趣和动力.
三、灵活运用
例2.我国是世界上严重缺水的国家之一,某市为了制定合理的节水方案,对家庭用水情况进行了调查,通过抽样,获得了某年100个家庭的月均用水量(单位:t),将数据按照[0,1),[1,2),[2,3),[3,4),[4,5)分成了5组,制成了如图所示频率分布直方图.
(1)求图a中的值;
(2)设该市有10万个家庭,估计全市月均用水量不低于3t的家庭数;
(3)假设同组的每个数据都用该组区间的中点值代替,估计全市家庭月均用水量的平均数.
解:
(1)因为频率分布直方图所有举行的面积之和为1,所以
(0.12+0.22+0.36+a+0.12)×1=1
解得A=0.18
(2)抽取的样本中,月均用水量不低于3t的家庭所占比例为
(a+0.12)×1=0.3
因此估计全市月均用水量不低于3t的家庭所占比例也为30%,所求家庭数为100000×30%=30000.
(3)因为
0.12×0.5+0.22×1.5+0.36×2.5+0.18×3.5+0.12×4.5=2.64,
估计全市家庭月均用水量的平均数为2.46.
【设计意图】
例2完整地描述出了用样本的分布估计总体的分布的过程;首先收集数据,然后用合适的形式显示样本数据,最后抽取其中的信息对总体进行预测.第(3)问要求按照区间中点的值来进行计算,理论上讲,也可以用区间左端点或者右端点的值来进行计算,但一般不这样做.
练习1:在一段时间内有2000辆车通过高速公路上的某处,现随机抽取其中的200辆进行车速统计,统计结果如右面的频率分布直方图所示.
(Ⅰ)求直方图中x的值;
(Ⅱ)若该处高速公路规定正常行驶速度为90km/h~120km/h,试估计2000辆车中,在这段时间内以正常速度通过该处的汽车约有多少辆.?
参考答案:(Ⅰ)x=0.02?(Ⅱ)2000×(0.030+0.035+0.020)=1700(辆)
四、归纳总结
体会样本与总体的关系,体验用样本的分布估计总体的分布.
用样本估计总体,21世纪的世界是海量数据存在并高速增长的世界,数据的重要性非同一般.这一大节特别梳理清楚数据、总体、样本这三者这间的关系,画频率分布直观图也好,计算样本平均数、样本标准差也好,……,都不是就是论事的讨论样本数据,而同时要体现“估计总体”,从而突出“用局部估计总体”的思想.
用样本估计总体
第二课时
教案
教学课时:第2课时
教学目标:
通过具体实例,学生体会样本与总体的关系,体验用样本的分布估计总体的分布.
教学重点:
样本的分布估计总体的分布.
教学难点:
用样本“估计总体”,?突出“用局部估计总体”的思想.
教学过程:
前面一节课,我们体会了可以用样本的数字特征估计总体的数字特征,那么,总体的分布是否也可以用样本的分布来近似刻画呢?
一、【尝试与发现】(课本80页)
通过对某中学1257名高一学生期中考试的数学成绩(具体数据参见课本85-87页)进行整理,可以得到如下数据,并由此可作出频率分布直方图和折线图,如图所示.
【学生活动1】
在附录的数据中抽取容量是100的样本,整理类似的表格,并制作频率分布直方图.
学生分成2组,选用随机抽样的方法分别抽取容量是100的样本,分别记为样本A,样本B?,分别得到如下的频数、频率对应表,它们的频率分布直方图,借助信息技术完成相应任务.
【设计意图】
这个活动意在让学生体会和感受统计的思想方法,学生经历和体验了数据收集、数据处理等过程,真正理解统计的思想方法.
回顾问题:总体的分布是否也可以用样本的分布来近似刻画呢?
解决问题:如果样本的容量恰当,抽样方法又合理,在容许一定误差存在的前提下,可以用样本的分布估计总体的分布.分布的估计一般也有误差,如果总体在每一组的频率记为P1,P2,……Pn,一般来说,
不等于零,同样,大数定律可以保证,当样本的容量越来越大时,上式很小的可能性将越来越大.
二、“大数据”简介
学生自行完成课本83页“大数据”阅读,对“大数据”价值的认识,有利于学生对未来职业的选择、个人发展规划的制定,激发学生学习的兴趣和动力.
三、灵活运用
例2.我国是世界上严重缺水的国家之一,某市为了制定合理的节水方案,对家庭用水情况进行了调查,通过抽样,获得了某年100个家庭的月均用水量(单位:t),将数据按照[0,1),[1,2),[2,3),[3,4),[4,5)分成了5组,制成了如图所示频率分布直方图.
(1)求图a中的值;
(2)设该市有10万个家庭,估计全市月均用水量不低于3t的家庭数;
(3)假设同组的每个数据都用该组区间的中点值代替,估计全市家庭月均用水量的平均数.
解:
(1)因为频率分布直方图所有举行的面积之和为1,所以
(0.12+0.22+0.36+a+0.12)×1=1
解得A=0.18
(2)抽取的样本中,月均用水量不低于3t的家庭所占比例为
(a+0.12)×1=0.3
因此估计全市月均用水量不低于3t的家庭所占比例也为30%,所求家庭数为100000×30%=30000.
(3)因为
0.12×0.5+0.22×1.5+0.36×2.5+0.18×3.5+0.12×4.5=2.64,
估计全市家庭月均用水量的平均数为2.46.
【设计意图】
例2完整地描述出了用样本的分布估计总体的分布的过程;首先收集数据,然后用合适的形式显示样本数据,最后抽取其中的信息对总体进行预测.第(3)问要求按照区间中点的值来进行计算,理论上讲,也可以用区间左端点或者右端点的值来进行计算,但一般不这样做.
练习1:在一段时间内有2000辆车通过高速公路上的某处,现随机抽取其中的200辆进行车速统计,统计结果如右面的频率分布直方图所示.
(Ⅰ)求直方图中x的值;
(Ⅱ)若该处高速公路规定正常行驶速度为90km/h~120km/h,试估计2000辆车中,在这段时间内以正常速度通过该处的汽车约有多少辆.?
参考答案:(Ⅰ)x=0.02?(Ⅱ)2000×(0.030+0.035+0.020)=1700(辆)
四、归纳总结
体会样本与总体的关系,体验用样本的分布估计总体的分布.
用样本估计总体,21世纪的世界是海量数据存在并高速增长的世界,数据的重要性非同一般.这一大节特别梳理清楚数据、总体、样本这三者这间的关系,画频率分布直观图也好,计算样本平均数、样本标准差也好,……,都不是就是论事的讨论样本数据,而同时要体现“估计总体”,从而突出“用局部估计总体”的思想.
