七年级数学9.1.2不等式的性质(2)课件PPT
文档属性
| 名称 | 七年级数学9.1.2不等式的性质(2)课件PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 238.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-27 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
不等式的基本性质1:
如果a >b,那么a±c>b±c.就是说,不等式两边都加上 (或减去)同一个数(或式子),不等号方向不变。
不等式基本性质2:
如果a >b,c > 0 ,那么 ac>bc(或 ) 就是说不等式的两边都乘以(或除以)同一个正数,不等号的方向不变。
不等式基本性质3:
如果a>b,c<0 那么ac将下列不等式化成x > a或 x < a 的形式,并说出根据.
(1) x- 7>26
(2) 3x < 2x +1
解:根据不等式的基本性质1 , 不等式两边都加上7,不等号方向不变,得, x >33
解:根据不等式的基本性质1,不等式两边都减去2x,不等号方向不变,得,x < 1
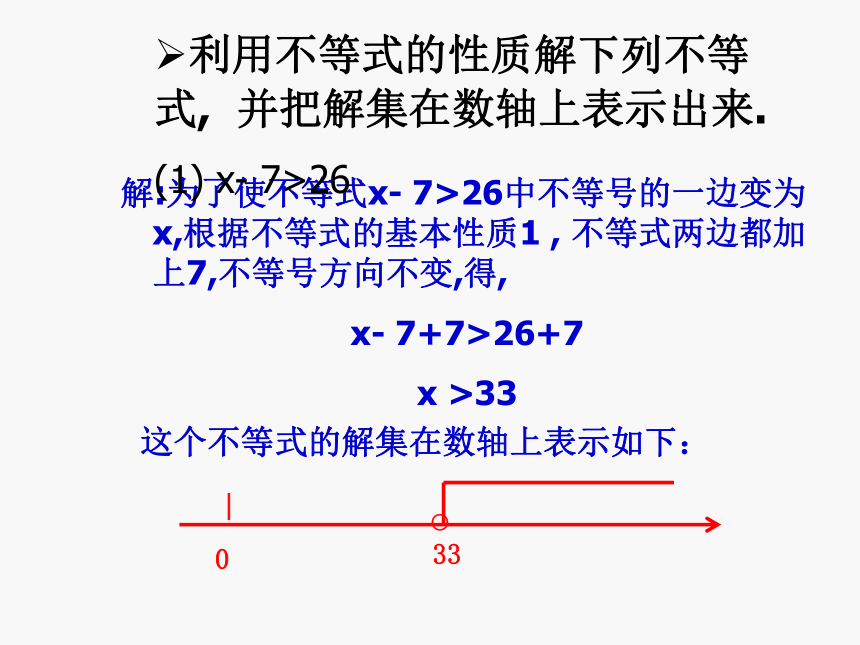
题目改为:利用不等式的性质解下列不等式, 并把解集在数轴上表示出来.
解:为了使不等式x- 7>26中不等号的一边变为x,根据不等式的基本性质1 , 不等式两边都加上7,不等号方向不变,得,
x- 7+7>26+7
x >33
这个不等式的解集在数轴上表示如下:
︱
0
利用不等式的性质解下列不等式, 并把解集在数轴上表示出来.
(1) x- 7>26
○
33
圣诞节到了,小明去买贺卡花了x元,买邮票花了3元,他总共花了10元,请问小明买贺卡花了多少元?(列方程求解)
解:由题意,得 x+3=10
移项,得 x =10-3
合并同类项,得 x =7
答:小明买贺卡花了7元.
移项法则的理论依据是
如果小明总共花的钱不足10元呢?根据题意你能列出一个式子吗?
移项要变号。
等式的性质1
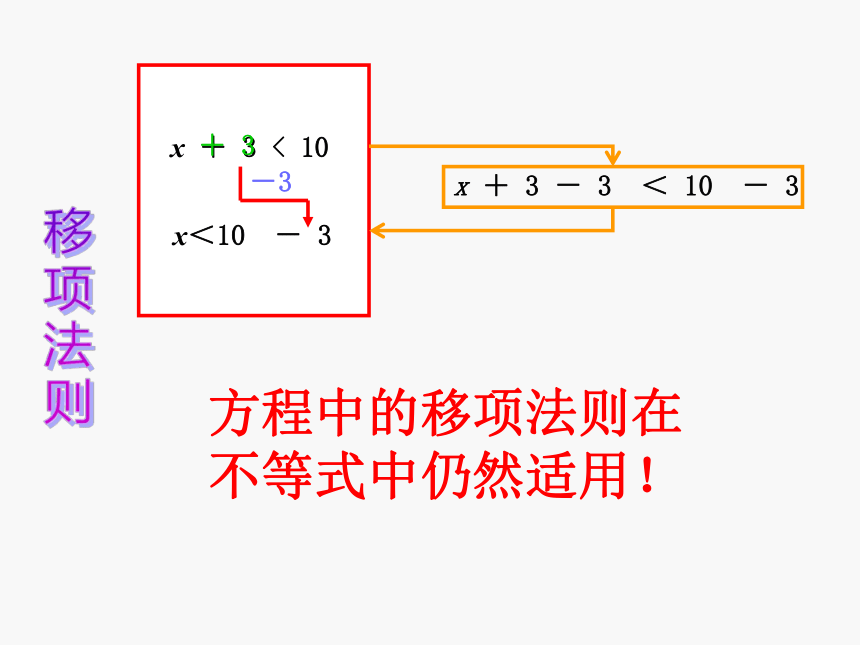
x+3<10
+3
-3
x + 3 < 10
x<10 - 3
+ 3
-3
x + 3 - 3 < 10 - 3
方程中的移项法则在不等式中仍然适用!
1
2
3
4
5
6
7
8
-1
-2
-3
-4
解: 移项得 x <10-3
例 1 解一元一次不等式 x + 3 < 10
即 x < 7
这个不等式的解集在数轴上表示如下:
0
问题1:实心小圆点和空心小圆圈分别在什么时候适用
解一元一次不等式 8x-2≤7x+3,并把它的解在数轴上表示出来。
例2
解:移项,得
0
1
2
3
4
5
6
7
-1
x
8x- 7x ≤3+2
∴ x ≤5
这个不等式的解集在数轴上表示如下:
思考:求满足不等式 8x-2≤7x+3 的正整数解
8x-2≤7x+3
8x-7x≤3+2
x + 3 < 10
x<10 - 3
+ 3
-3
7x
-7x
-2
+2
再说一遍:移项要变号,不影响不等号的方向
填 空:
解不等式:-2x+1>3-3x
解: -2x+1> 3 - 3x
移项,得 -2x >3
合并,得 >
+3x
-1
x
2
例3 解不等式
3(1-x)>2(1-2x)
解: 去括号,得 3-3 x >2-4x
移项,得 -3 x +4x >-3+2
合并同类项,得 x >-1
∴原不等式的解集是x >-1
比一比,谁做得又快又好!
(1)x+4>3
(2)7x+6 ≥ 6x+3
(3)7x-1 ≤ 6x+1
(4)3-5x < 2(2-3x)
解下列不等式,并把它们的解集在数轴上 表示出来。
例
解不等式3+3x>2+4x
解:移项,得 3-2> 4x-3x
合并同类项,得 1>x
∴ 原不等式的解集是 x<1
写不等式的解集时,要把表示未知数的字母写在不等号的左边。
例如
1、求不等式3(x-3)+6 < 2x+1的正整数解。
思考
2、X取什么值时,代数式x+ 的值。
(1)大于0 (2)不小于-
求满足不等式
2(1-2X)-5+X<1-2X的负整数解
m为何值时,方程 的解是非正数.
1、不等式性质1:不等式的两边__加上或__减去__一个数或式,所得到的不等式____.
都
都
同
仍成立
2、不等式移项法则:把不等式的任何一项的_____后,从_______的___移到_______,所得到的不等式仍成立。
符号改变
一边
另一边
不等号
教科书
P134 第6题、第9题
P135 第12题
不等式的基本性质1:
如果a >b,那么a±c>b±c.就是说,不等式两边都加上 (或减去)同一个数(或式子),不等号方向不变。
不等式基本性质2:
如果a >b,c > 0 ,那么 ac>bc(或 ) 就是说不等式的两边都乘以(或除以)同一个正数,不等号的方向不变。
不等式基本性质3:
如果a>b,c<0 那么ac
(1) x- 7>26
(2) 3x < 2x +1
解:根据不等式的基本性质1 , 不等式两边都加上7,不等号方向不变,得, x >33
解:根据不等式的基本性质1,不等式两边都减去2x,不等号方向不变,得,x < 1
题目改为:利用不等式的性质解下列不等式, 并把解集在数轴上表示出来.
解:为了使不等式x- 7>26中不等号的一边变为x,根据不等式的基本性质1 , 不等式两边都加上7,不等号方向不变,得,
x- 7+7>26+7
x >33
这个不等式的解集在数轴上表示如下:
︱
0
利用不等式的性质解下列不等式, 并把解集在数轴上表示出来.
(1) x- 7>26
○
33
圣诞节到了,小明去买贺卡花了x元,买邮票花了3元,他总共花了10元,请问小明买贺卡花了多少元?(列方程求解)
解:由题意,得 x+3=10
移项,得 x =10-3
合并同类项,得 x =7
答:小明买贺卡花了7元.
移项法则的理论依据是
如果小明总共花的钱不足10元呢?根据题意你能列出一个式子吗?
移项要变号。
等式的性质1
x+3<10
+3
-3
x + 3 < 10
x<10 - 3
+ 3
-3
x + 3 - 3 < 10 - 3
方程中的移项法则在不等式中仍然适用!
1
2
3
4
5
6
7
8
-1
-2
-3
-4
解: 移项得 x <10-3
例 1 解一元一次不等式 x + 3 < 10
即 x < 7
这个不等式的解集在数轴上表示如下:
0
问题1:实心小圆点和空心小圆圈分别在什么时候适用
解一元一次不等式 8x-2≤7x+3,并把它的解在数轴上表示出来。
例2
解:移项,得
0
1
2
3
4
5
6
7
-1
x
8x- 7x ≤3+2
∴ x ≤5
这个不等式的解集在数轴上表示如下:
思考:求满足不等式 8x-2≤7x+3 的正整数解
8x-2≤7x+3
8x-7x≤3+2
x + 3 < 10
x<10 - 3
+ 3
-3
7x
-7x
-2
+2
再说一遍:移项要变号,不影响不等号的方向
填 空:
解不等式:-2x+1>3-3x
解: -2x+1> 3 - 3x
移项,得 -2x >3
合并,得 >
+3x
-1
x
2
例3 解不等式
3(1-x)>2(1-2x)
解: 去括号,得 3-3 x >2-4x
移项,得 -3 x +4x >-3+2
合并同类项,得 x >-1
∴原不等式的解集是x >-1
比一比,谁做得又快又好!
(1)x+4>3
(2)7x+6 ≥ 6x+3
(3)7x-1 ≤ 6x+1
(4)3-5x < 2(2-3x)
解下列不等式,并把它们的解集在数轴上 表示出来。
例
解不等式3+3x>2+4x
解:移项,得 3-2> 4x-3x
合并同类项,得 1>x
∴ 原不等式的解集是 x<1
写不等式的解集时,要把表示未知数的字母写在不等号的左边。
例如
1、求不等式3(x-3)+6 < 2x+1的正整数解。
思考
2、X取什么值时,代数式x+ 的值。
(1)大于0 (2)不小于-
求满足不等式
2(1-2X)-5+X<1-2X的负整数解
m为何值时,方程 的解是非正数.
1、不等式性质1:不等式的两边__加上或__减去__一个数或式,所得到的不等式____.
都
都
同
仍成立
2、不等式移项法则:把不等式的任何一项的_____后,从_______的___移到_______,所得到的不等式仍成立。
符号改变
一边
另一边
不等号
教科书
P134 第6题、第9题
P135 第12题
