七年级数学镶嵌
图片预览








文档简介
(共34张PPT)
镶 嵌
好漂亮的地板!这是怎么铺设的 一点空隙也没有.
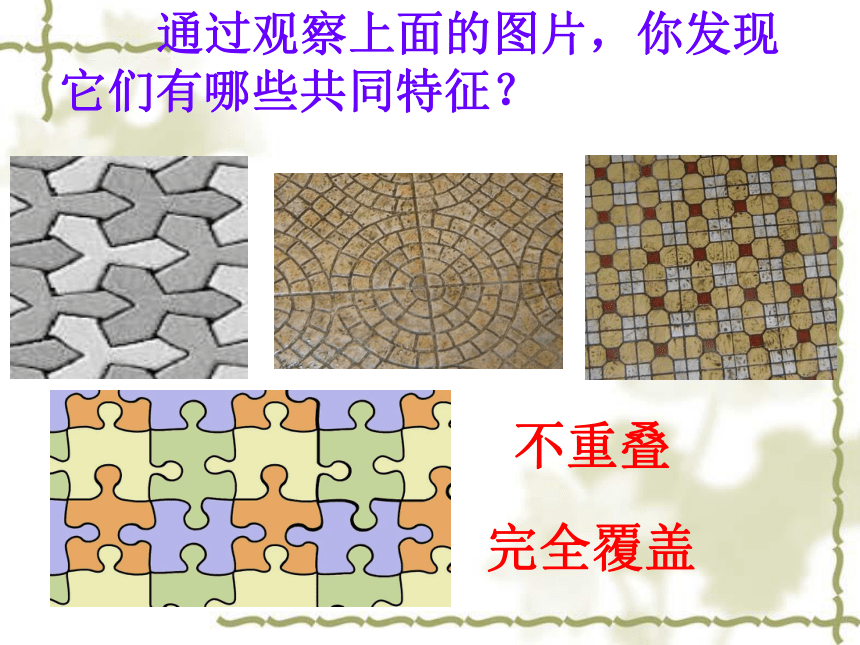
通过观察上面的图片,你发现它们有哪些共同特征?
不重叠
完全覆盖
从数学角度看,用一些不重叠摆放的多边形把平面的一部分完全覆盖,通常把这类问题叫做覆盖平面(或平面镶嵌)的问题.
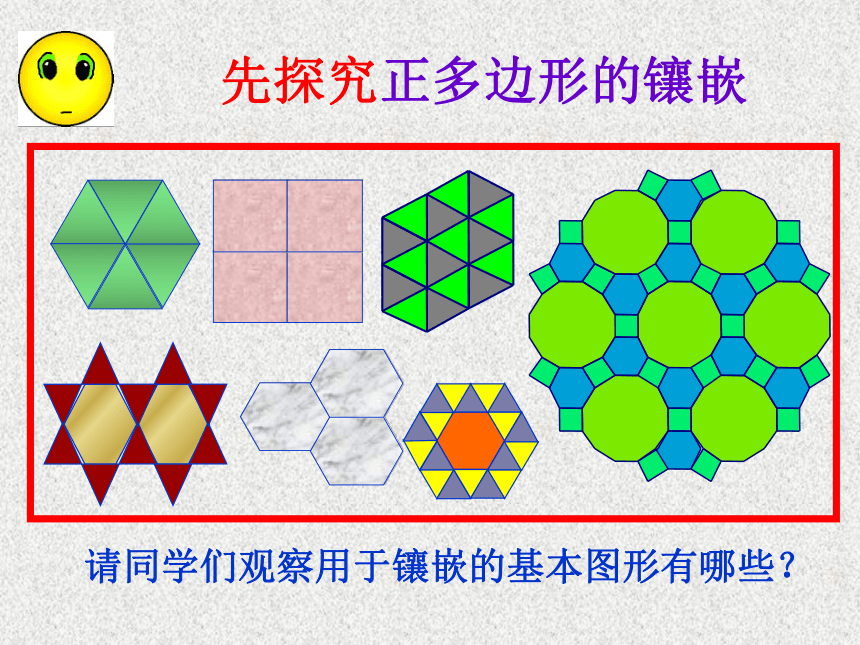
请同学们观察用于镶嵌的基本图形有哪些?
先探究正多边形的镶嵌
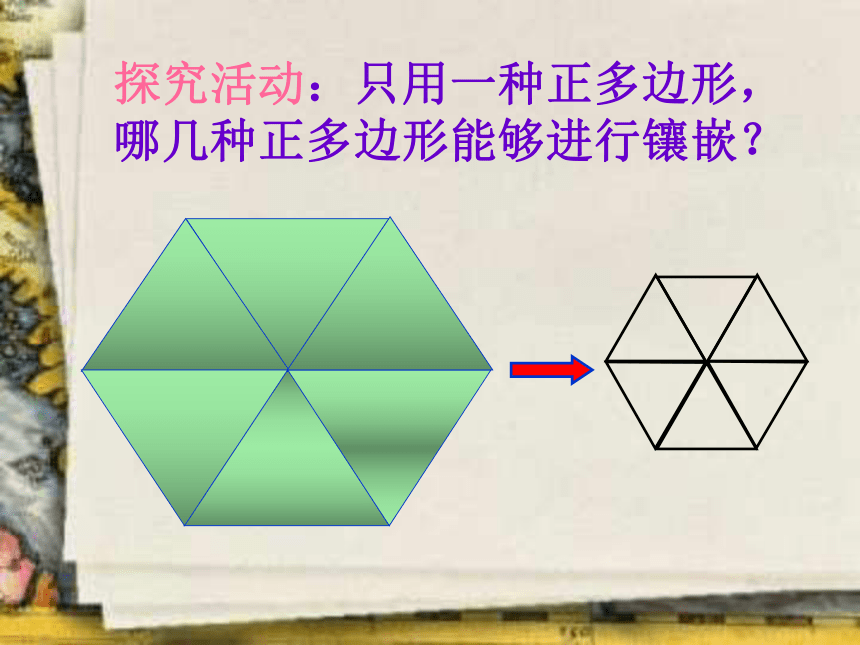
探究活动:只用一种正多边形,哪几种正多边形能够进行镶嵌?
收 集 整 理 数 据 正n边形 拼图 每个内角的度数 使用正多边形的个数k 结论
能镶嵌
能镶嵌
不能镶嵌
不能镶嵌
能镶嵌
K= 6
K= 4
K= 3
K= 4
K= 3
60°
90°
108°
108°
120°
n =3
n =6
n =4
n =5
分 析 数 据 正n边形 拼图 每个内角的度数
与360°的关系 结论
n=3
n=4
n=5
n=6
能镶嵌
不能镶嵌
不能镶嵌
能镶嵌
6×60°= 360°
4×90°= 360°
4×108°> 360°
3×120°= 360°
3×108°< 360°
能镶嵌
得出结论:
如果一个正多边形可以进行镶嵌,那么内角一定是360°的约数(或360°一定是这个多边形内角的整数倍)!
思考:用下列正多边形能镶嵌吗?
正7边形?
正十边形?
正20边形?
小试牛刀
如果用两种正多边形进行镶嵌需要满足什么条件?
小颖家正在为新房子装修,在他的房间里,他想用正三角形和另一种正多边形镶嵌成地板,他有哪些选择?
正多边形 拼 图
和
和
3×60°+ 2 ×90°= 360°
3×60+2 ×90°=360°
4×60+1 ×120°=360°
正三角形
正四边形
正三角形
正六角形
得出结论:
用两种正多边形镶嵌的规律:拼接在同一个点的各个角的和恰好等于360°(周角)。
正五边形和正十边形能否镶嵌
正四边形和正八边形能否镶嵌
牛刀小试
得出结论:
用两种正多边形镶嵌的规律:拼接在同一个点的各个角的和恰好等于360°(周角)。
两种正多边形的边长相等.
某足球场需铺设草皮。现有正三角形、正四边形、正六边形、正八边形、四种形状的草皮,假如你是名设计师,你有哪些选择
拓展与应用
实验活动:
1、用一种任意三角形,怎样进行
镶嵌?
2、用一种任意四边形,怎样进行
镶嵌?
3、用一种任意梯形,怎样进行
镶嵌?
收获与启示
什么叫镶嵌
用一种正多边形和两种正多边形镶嵌的规律
数学试验对学习的帮组和启发
请你为小颖同学所选择的正三角形的地板配上另一种正多边形使它们能够镶嵌在小颖的房间里!并写出所有的设计方案!
课后思考:
资料1:用正多边形进行平面镶嵌只有以下这17组解。
有书记载说明这17组解是1924年一个叫波尔亚的人给出的。实际上早在此之前,西班牙阿尔汉布拉宫的装饰已经一个不少地制出了这些图样,真是令人叹为观止。
第一页
第二页
资料2:石子路镶嵌图案最多的图林
在北京故官御花园内,有许多颜色不同的细石子砌成的各种美丽图案的花石子路,据统计全园花石子路上的图案约有900幅,可以说是中国拥有石子路镶嵌图案最多的图林了。这些石子路图案的组成,是把全园作为一个整体来考虑设计的,因此显得极为统一协调。但是每幅图案又有它的独立的面貌,内容各异,图案的内容有人物、风景、花卉、博古等,种类繁多。其中的“颐和春色”、“关黄对刀”、“鹤鹿同春”等图案,造型优美,动态活泼、构图别致,色彩分明,沿路观赏,美不胜收。
第一页
第二页
Good Good Study ! Day Day Up !
镶 嵌
好漂亮的地板!这是怎么铺设的 一点空隙也没有.
通过观察上面的图片,你发现它们有哪些共同特征?
不重叠
完全覆盖
从数学角度看,用一些不重叠摆放的多边形把平面的一部分完全覆盖,通常把这类问题叫做覆盖平面(或平面镶嵌)的问题.
请同学们观察用于镶嵌的基本图形有哪些?
先探究正多边形的镶嵌
探究活动:只用一种正多边形,哪几种正多边形能够进行镶嵌?
收 集 整 理 数 据 正n边形 拼图 每个内角的度数 使用正多边形的个数k 结论
能镶嵌
能镶嵌
不能镶嵌
不能镶嵌
能镶嵌
K= 6
K= 4
K= 3
K= 4
K= 3
60°
90°
108°
108°
120°
n =3
n =6
n =4
n =5
分 析 数 据 正n边形 拼图 每个内角的度数
与360°的关系 结论
n=3
n=4
n=5
n=6
能镶嵌
不能镶嵌
不能镶嵌
能镶嵌
6×60°= 360°
4×90°= 360°
4×108°> 360°
3×120°= 360°
3×108°< 360°
能镶嵌
得出结论:
如果一个正多边形可以进行镶嵌,那么内角一定是360°的约数(或360°一定是这个多边形内角的整数倍)!
思考:用下列正多边形能镶嵌吗?
正7边形?
正十边形?
正20边形?
小试牛刀
如果用两种正多边形进行镶嵌需要满足什么条件?
小颖家正在为新房子装修,在他的房间里,他想用正三角形和另一种正多边形镶嵌成地板,他有哪些选择?
正多边形 拼 图
和
和
3×60°+ 2 ×90°= 360°
3×60+2 ×90°=360°
4×60+1 ×120°=360°
正三角形
正四边形
正三角形
正六角形
得出结论:
用两种正多边形镶嵌的规律:拼接在同一个点的各个角的和恰好等于360°(周角)。
正五边形和正十边形能否镶嵌
正四边形和正八边形能否镶嵌
牛刀小试
得出结论:
用两种正多边形镶嵌的规律:拼接在同一个点的各个角的和恰好等于360°(周角)。
两种正多边形的边长相等.
某足球场需铺设草皮。现有正三角形、正四边形、正六边形、正八边形、四种形状的草皮,假如你是名设计师,你有哪些选择
拓展与应用
实验活动:
1、用一种任意三角形,怎样进行
镶嵌?
2、用一种任意四边形,怎样进行
镶嵌?
3、用一种任意梯形,怎样进行
镶嵌?
收获与启示
什么叫镶嵌
用一种正多边形和两种正多边形镶嵌的规律
数学试验对学习的帮组和启发
请你为小颖同学所选择的正三角形的地板配上另一种正多边形使它们能够镶嵌在小颖的房间里!并写出所有的设计方案!
课后思考:
资料1:用正多边形进行平面镶嵌只有以下这17组解。
有书记载说明这17组解是1924年一个叫波尔亚的人给出的。实际上早在此之前,西班牙阿尔汉布拉宫的装饰已经一个不少地制出了这些图样,真是令人叹为观止。
第一页
第二页
资料2:石子路镶嵌图案最多的图林
在北京故官御花园内,有许多颜色不同的细石子砌成的各种美丽图案的花石子路,据统计全园花石子路上的图案约有900幅,可以说是中国拥有石子路镶嵌图案最多的图林了。这些石子路图案的组成,是把全园作为一个整体来考虑设计的,因此显得极为统一协调。但是每幅图案又有它的独立的面貌,内容各异,图案的内容有人物、风景、花卉、博古等,种类繁多。其中的“颐和春色”、“关黄对刀”、“鹤鹿同春”等图案,造型优美,动态活泼、构图别致,色彩分明,沿路观赏,美不胜收。
第一页
第二页
Good Good Study ! Day Day Up !
