切线的判定与性质

(共29张PPT)
人教版九年级上册
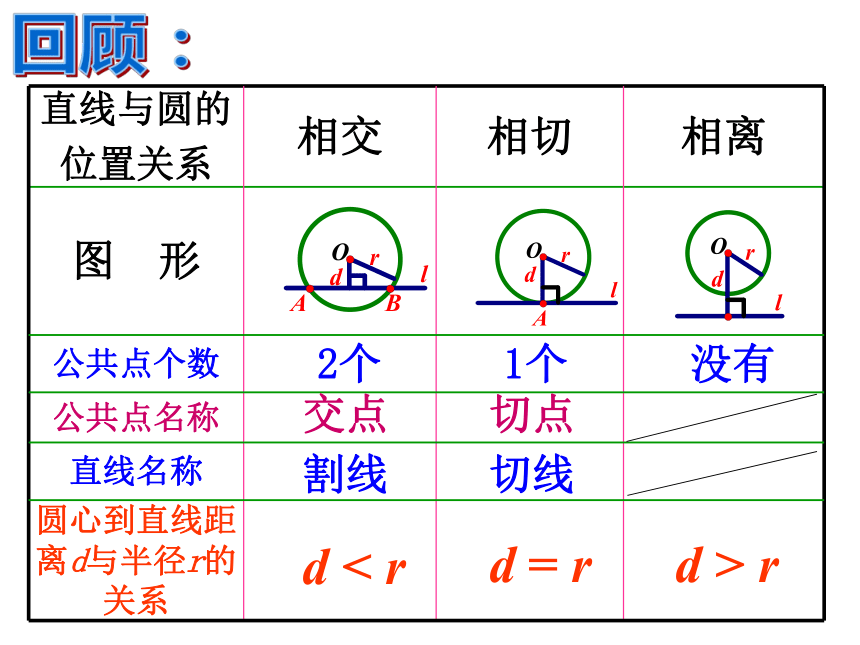
直线与圆的
位置关系 相交 相切 相离
图 形
公共点个数
公共点名称
直线名称
圆心到直线距离d与半径r的关系
2个
交点
割线
1个
切点
切线
d < r
d = r
d > r
没有
下雨天转动雨伞时飞出的水，以及在砂轮上打磨工件飞出的火星，均沿着圆的切线的方向飞出．
1 当你在下雨天快速转动雨伞时水飞出的方向是什么方向？
2 砂轮打磨零件飞出火星的方向是什么方向？
生活中的数学
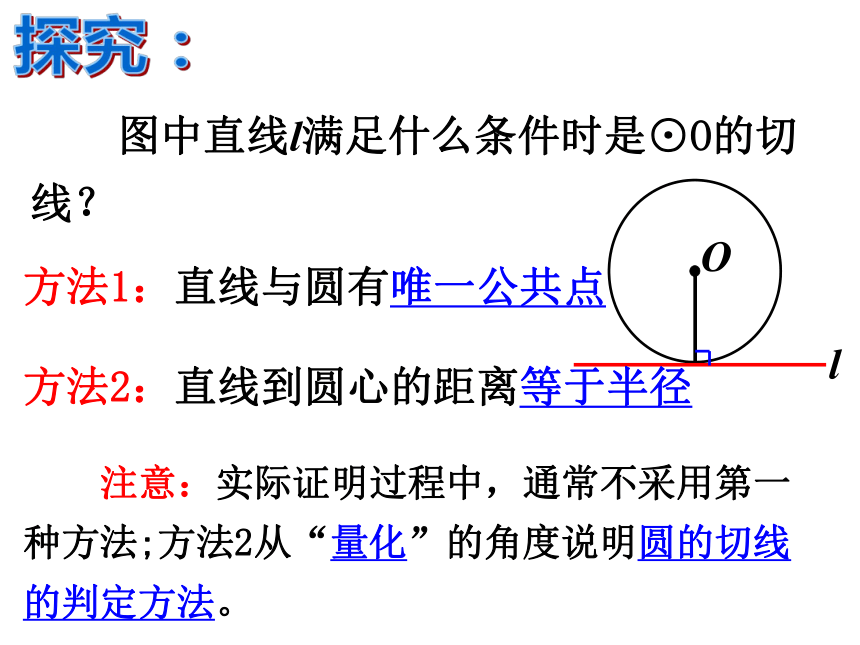
图中直线l满足什么条件时是⊙O的切线？
O
l
方法1：直线与圆有唯一公共点
方法2：直线到圆心的距离等于半径
注意：实际证明过程中，通常不采用第一种方法;方法2从“量化”的角度说明圆的切线的判定方法。
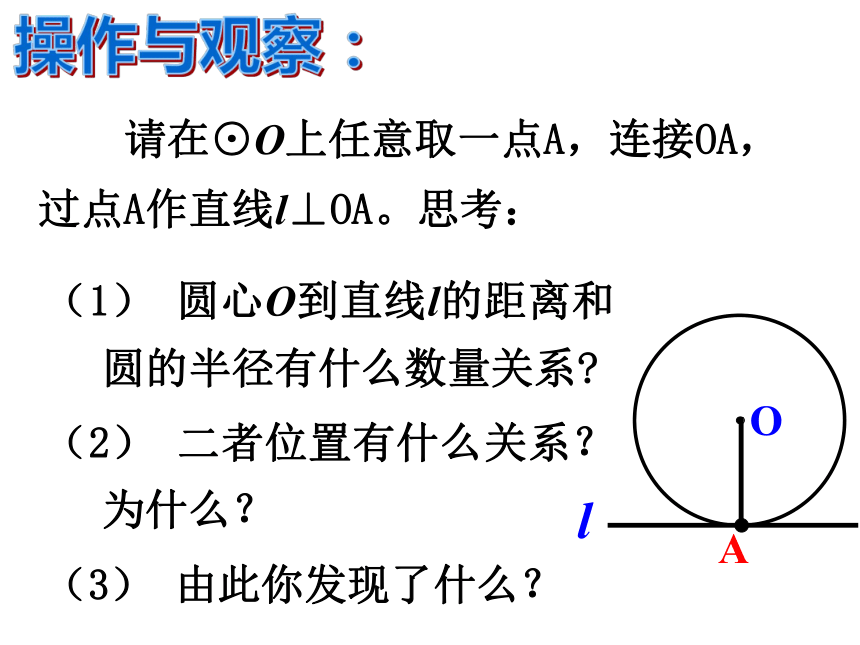
（1） 圆心O到直线l的距离和圆的半径有什么数量关系
（2） 二者位置有什么关系？为什么？
（3） 由此你发现了什么？
O
请在⊙O上任意取一点A，连接OA，过点A作直线l⊥OA。思考：
l
A
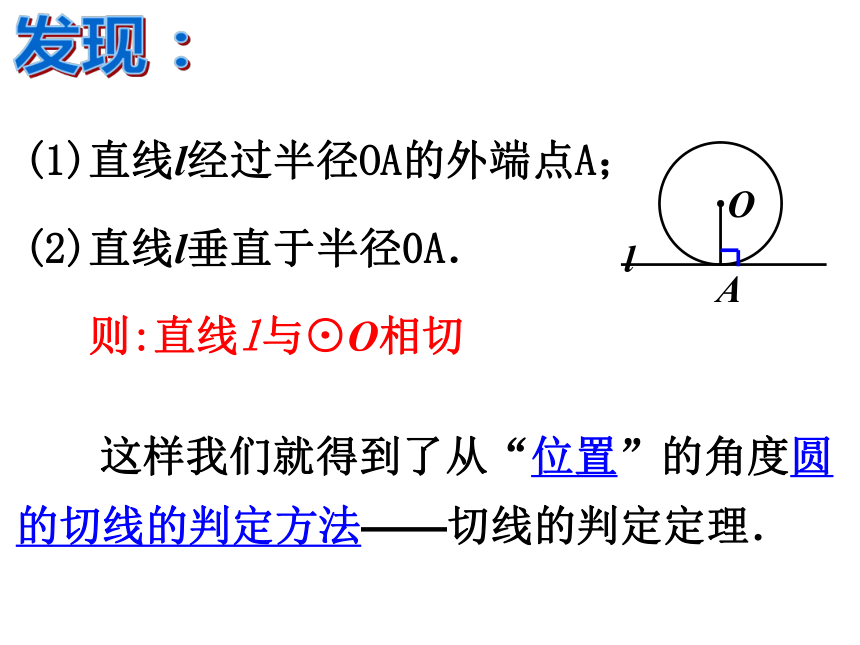
(1)直线l经过半径OA的外端点A；
(2)直线l垂直于半径0A．
则:直线l与⊙O相切
这样我们就得到了从“位置”的角度圆的切线的判定方法——切线的判定定理．
A
O
l
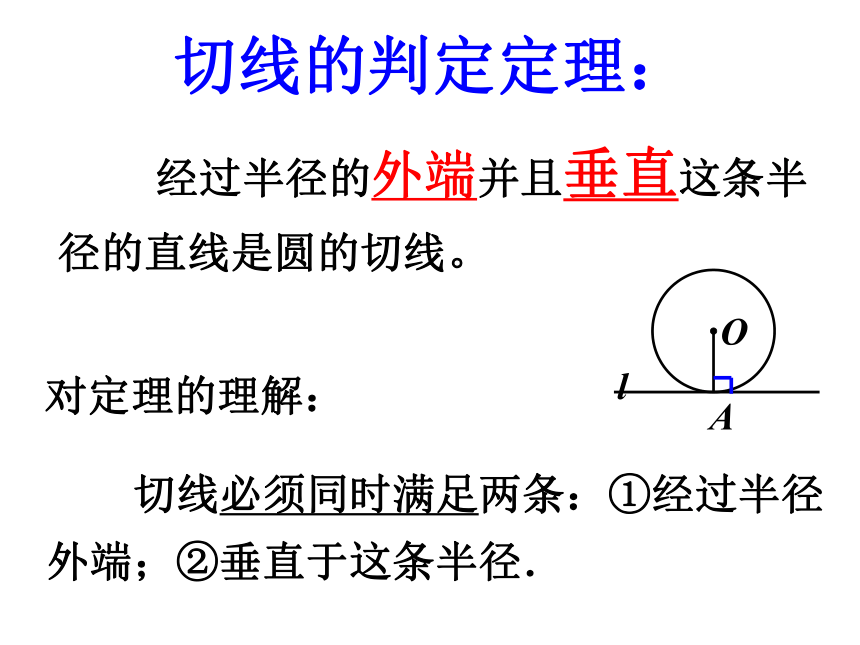
切线的判定定理：
经过半径的外端并且垂直这条半径的直线是圆的切线。
对定理的理解：
切线必须同时满足两条：①经过半径外端；②垂直于这条半径．
A
O
l
O
r
l
A
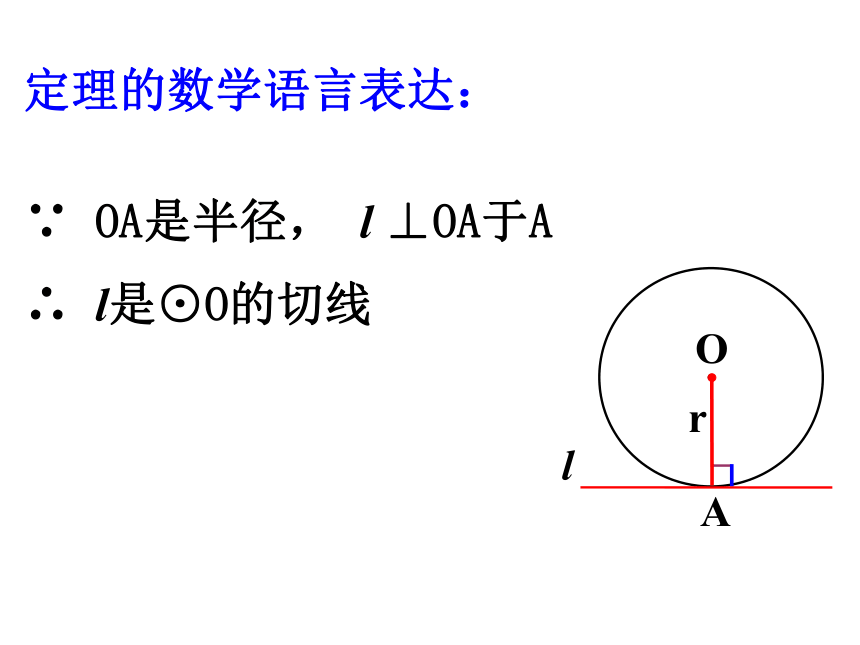
∵ OA是半径， l ⊥OA于A
∴ l是⊙O的切线
定理的数学语言表达：
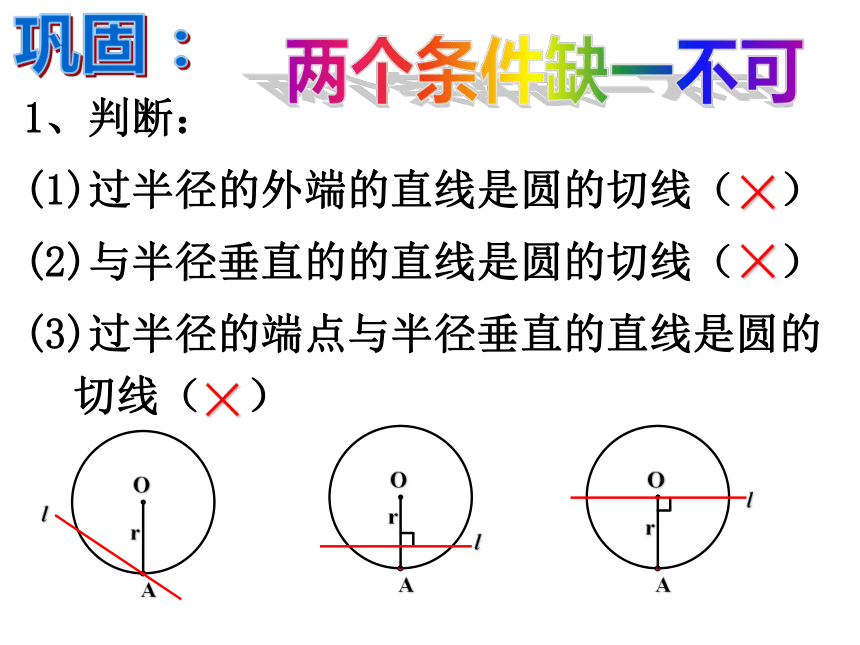
1、判断：
(1)过半径的外端的直线是圆的切线（ ）
(2)与半径垂直的的直线是圆的切线（ ）
(3)过半径的端点与半径垂直的直线是圆的切线（ ）
×
×
×
O
r
l
A
O
r
l
A
O
r
l
A
切线的判定方法有三种：
①直线与圆有唯一公共点；
②直线到圆心的距离等于该圆的半径；
③切线的判定定理．即
经过半径的外端并且垂直这条半径的直线是圆的切线.
判定直线与圆相切有哪些方法？
例1 如图，已知：直线AB经过⊙O上的点C，
并且OA=OB，CA=CB。
求证：直线AB是⊙O的切线。
O
B
A
C
分析：由于AB过⊙O上的点C，所以连接OC，只要证明AB⊥OC即可。
例2 如图，已知：O为∠BAC平分线上一
点，OD⊥AB于D,以O为圆心，OD为半径作
⊙O。
求证：⊙O与AC相切。
O
A
B
C
E
D
O
B
A
C
O
A
B
C
E
D
例1与例2的证法有何不同
(1)如果已知直线经过圆上一点,则连结这点和圆心,得到辅助半径,再证所作半径与这直线垂直.简记为：有交点，连半径,证垂直.
(2)如果已知条件中不知直线与圆是否有公共点,则过圆心作直线的垂线段,再证垂线段长等于半径长.简记为：无交点,作垂直,证半径.
2、如图,△ABC中,AB=AC,AO⊥BC于O，OE⊥AC于E,以O为圆心,OE为半径作⊙O.
求证：AB是⊙O的切线.
F
E
C
O
B
A
3、如图,AB是⊙O的直径,点D在AB的延长线上,BD=OB,点C在⊙O上, ∠CAB=30°.
求证:DC是⊙O的切线.
A
B
C
D
O
如图，如果直线l是⊙O的切线，切点为A，那么半径OA与直线l是不是一定垂直呢？
O
A
l
∵ l是⊙O的切线，切点为A
∴ l ⊥OA
切线的性质定理：圆的切线垂直于过切点的半径。
O
A
l
①过半径外端;
②垂直于这条半径.
切线
①圆的切线;
②过切点的半径.
切线垂直于半径
切线判定定理：
切线性质定理：
O
A
l
1、如图, ⊙O切PB于点B,PB=4,PA=2,则⊙O的半径多少？
注：已知切线、切点，则连接半径，应用切线的性质定理得到垂直关系，从而应用勾股定理计算。
2、如图，AB、AC分别切⊙O于B、C，若∠A=600，点P是圆上异于B、C的一动点，则∠BPC的度数是（ ） A、600 B、1200 C、600或1200 D、1400或600
B
P
C
A
O
1、知识：切线的判定定理．着重分析了定理成立的条件，在应用定理时，注重两个条件缺一不可．
2、方法：判定一条直线是圆的切线的三种方法：
(1) 根据切线定义判定．即与圆有唯一公共点的直线是圆的切线.
(2)根据圆心到直线的距离来判定，即与圆心的距离等于圆的半径的直线是圆的切线．
(3)根据切线的判定定理来判定．
其中(2)和(3)本质相同，只是表达形式不同．解题时，灵活选用其中之一．
谈谈今天的收获
1. 判定切线的方法有哪些？
直线l
与圆有唯一公共点
与圆心的距离等于圆的半径
经过半径外端且垂直这条半径
l是圆的切线
2. 证明圆的切线常用辅助线作法：
⑴连半径，证垂直
⑵作垂直，证半径
l是圆的切线
l是圆的切线
切线的性质定理：圆的切线垂直于过切点的半径。
O
A
l
例1 如图,AB是⊙O的直径, ⊙O过BC的中点D,
DE⊥AC.求证:DE是⊙O是切线.
证明:连接OD. ∵BD=CD,OA=OB,
∴OD是△ABC的中位线,
∴OD//AC.
又∵∠DEC=90
∴∠ODE=90
又∵D在圆周上,
∴DE是⊙O是切线..
A
O
B
D
C
E
例2 如图. AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.
求证:AC平分∠DAB.
A
B
O
C
D
证明:连接OC,
∴OC⊥CD.
又∵AD⊥CD,
∴OC//AD.由此得 ∠ACO=∠CAD.
∵OC=OA.
∴ ∠CAO=∠ACO.
∴ ∠CAD=∠CAO.
故AC平分∠DAB.
∵CD是⊙O的切线,
2.已知:OA和OB是⊙O的半径,并且OA⊥OB,P是OA
上任意一点,BP的延长线交⊙O于Q.过Q作⊙O的切
线交OA的延长线于R,.
求证:RP=RQ
B
O
P
A
R
Q
∠AQO= ∠APQ
3.AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD.
求证:DC是⊙O的切线.
A
O
B
C
D
1
3
2
4
△COD与COB全等
1、矩形的两边长分别为2.5和5，若以较长一边为直径作半圆，则矩形的各边与半圆相切的线段最多有（ ）
A、0条 B、 1条 C、 2条 D、 3条
D