湖南省长沙市明德教育集团2020-2021学年八年级下学期期末考试数学试题(word版含答案)
文档属性
| 名称 | 湖南省长沙市明德教育集团2020-2021学年八年级下学期期末考试数学试题(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 601.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-08 00:00:00 | ||
图片预览


文档简介
明德教育集团期末考试
八年级
数学试卷
20-21学年第二学期
时量:120分钟
满分:120
分
一、选择题(在下列各题的四个选项中,只有一项是符合题意的,请在答题卡中填涂符合题意的选项,本题共10题,每小题3分,共30分)
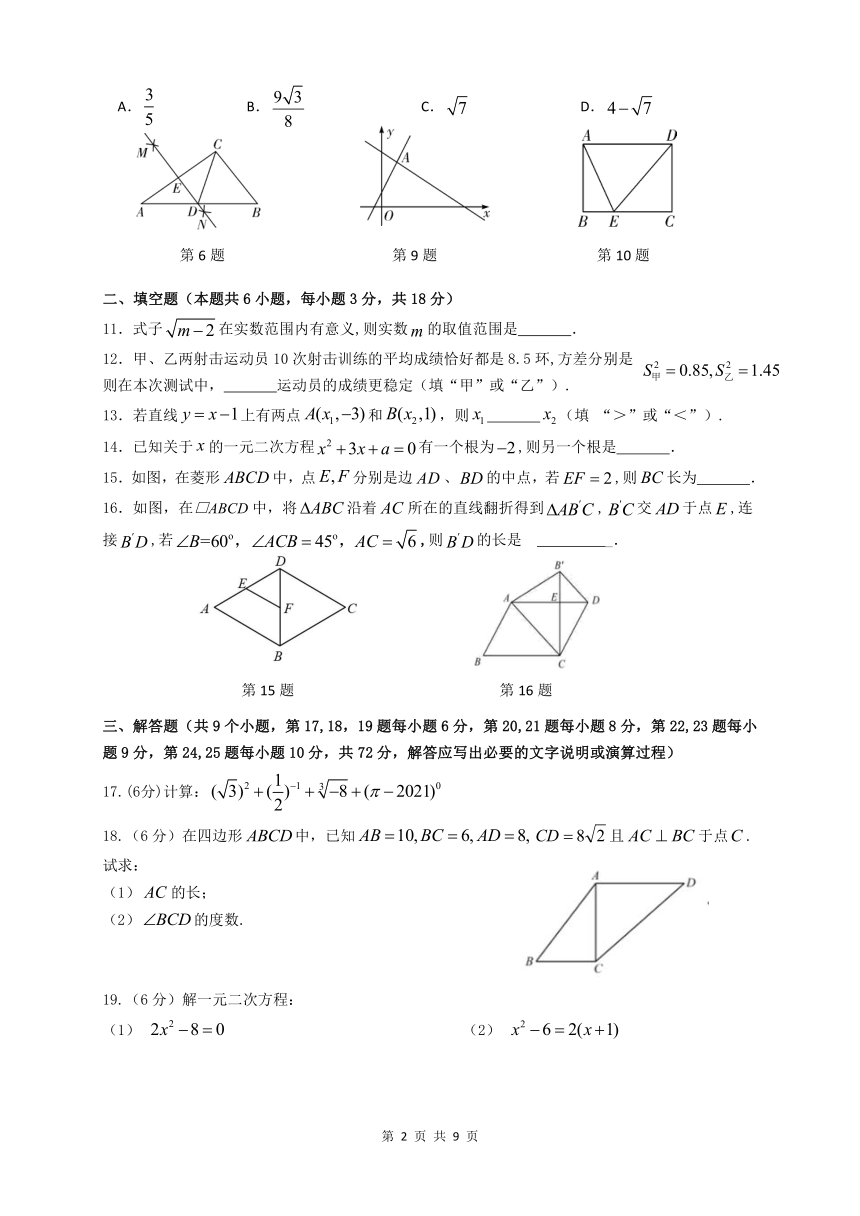
1.如图,下列的四个图象中,不能表示是的函数图象的是(
).
A.
B.
C.
D.
2.下列运算结果正确的是(
)
A.
B.
C.
D.
3.下列各组数中,不能构成直角三角形的一组是
(
)
A.7,24,25
B.,4,5
C.3,4,5
D.4,5,6
4.在□ABCD中,如果,那么的大小是(
)
A.70°
B.75°
C.40°
D.20°
5.为了向建党一百周年献礼,我市中小学生开展了图说党史比赛.某参赛小组名同学的成绩(单位:分)分别为:关于这组数据,下列说法错误的是(
)
A.众数是
B.中位数是
C.平均数是
D.方差是
6.正方形具有而菱形不具有的性质是(
)
A.对角相等
B.对角线互相平分
C.对角线相等
D.对角线互相垂直
7.如图,在中,,分别以点A和点为圆心,以大于长为半径画弧,两弧交于点和点,作直线交于点,交于点,连接,则长为( )
A.3
B.2.5
C.2
D.1.5
8.对于一元二次方程,则它根的情况为(
)
A.没有实数根
B.两根之和是
C.两根之积是
D.有两个不相等的实数根
9.如图,直线和直线相交于点,则关于的不等式的解集为(
)
A.
B.
C.
D.
10.如图,在矩形中,,点在边上,连接,若平分,则的长为(
)
A.
B.
C.
D.
二、填空题(本题共6小题,每小题3分,共18分)
11.式子在实数范围内有意义,则实数的取值范围是
.
12.甲、乙两射击运动员10次射击训练的平均成绩恰好都是8.5环,方差分别是
则在本次测试中,
运动员的成绩更稳定(填“甲”或“乙”).
13.若直线上有两点和,则
(填
“>”或“<”).
14.已知关于的一元二次方程有一个根为,则另一个根是
.
15.如图,在菱形中,点分别是边、的中点,若,则长为
.
16.如图,在□ABCD中,将沿着所在的直线翻折得到,交于点,连接,若,则的长是
_.
三、解答题(共9个小题,第17,18,19题每小题6分,第20,21题每小题8分,第22,23题每小题9分,第24,25题每小题10分,共72分,解答应写出必要的文字说明或演算过程)
17.(6分)计算:
18.(6分)在四边形中,已知且于点.
试求:
(1)的长;
(2)的度数.
19.(6分)解一元二次方程:
(1)
(2)
20.(
8分)某校要选举一名学生会主席,先对甲、乙、丙三名候选人进行了笔试和面试,成绩如下表,又进行了学生投票,每个学生都投了一张票,且选票上只写了三名候选人中的一名,每张选票记0.5分,对选票进行统计后,绘有如图1,图2尚不完整的统计图.
请完成下列问题;
(1)乙的得票率是
,选票的总数为
__;
(2)补全图2的条形统计图;
(3)根据实际情况,学校选取票数最多的两位学生,从笔试、面试、学生投票三项得分按2∶4∶4的比例确定每人最终成绩,高者当选,请通过计算说明,哪位候选人当选?
(8分)点在第一象限,且,点的坐标为,设的面积为.
用含的式子表示,写出的取值范围,画出函数的图象;
当点的横坐标为时,的面积是多少?
22.(9分)如图,□ABCD的对角线,相交于点,是等边三角形,.
(1)求证:□ABCD是矩形;
(2)求点到线段的距离.
23.(9分)为了积极响应新旧功能转换,提高公司的经济效益,某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为35万元时,年销售量为550台;每台售价为40万元时,年销售量为500台,假定该设备的年销售量(单位:台)和销售单价(单位:万元)成一次函数关系.
求年销售量与销售单价的函数关系式;
根据相关规定,此设备的销售单价不得高于60万元,如果该公司想获得8000万元的年利润,则该设备的销售单价应为多少万元?
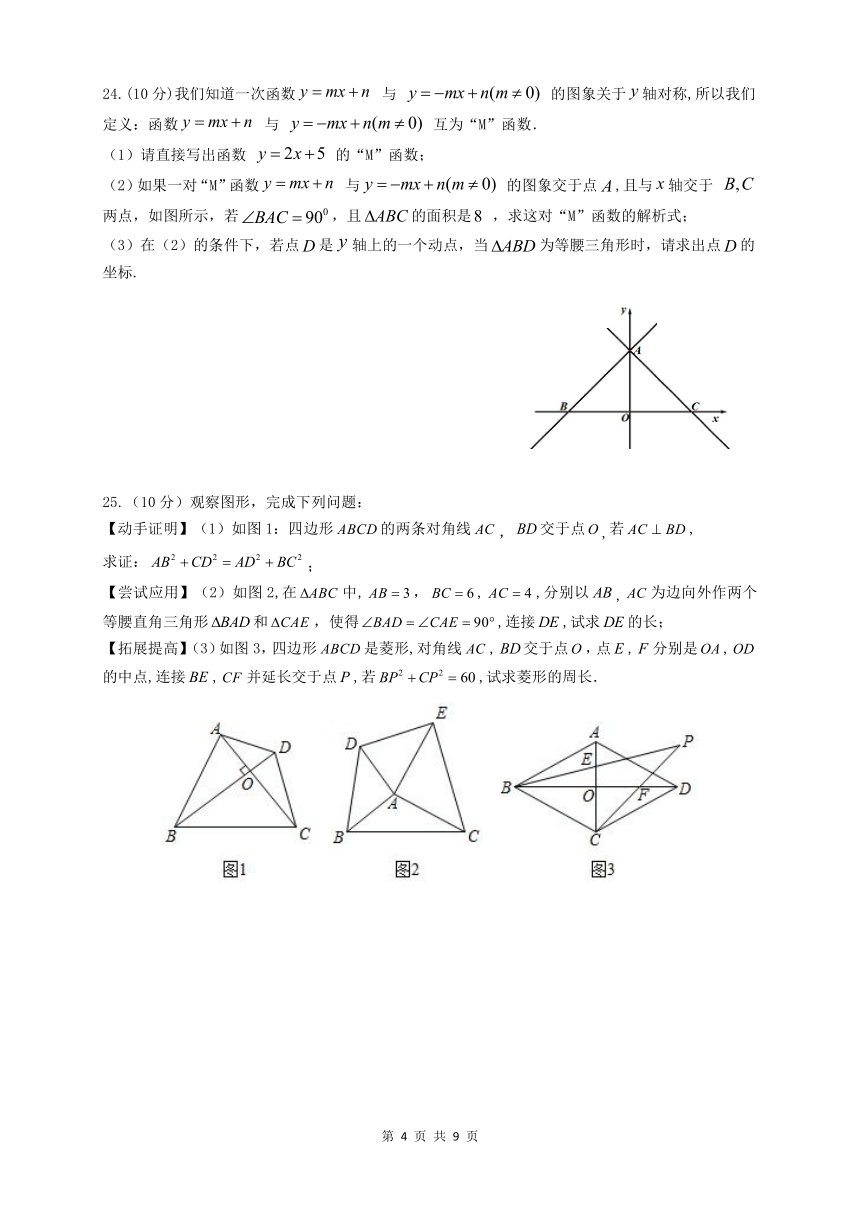
24.(10分)我们知道一次函数
与
的图象关于轴对称,所以我们定义:函数
与
互为“M”函数.
(1)请直接写出函数
的“M”函数;
(2)如果一对“M”函数
与
的图象交于点,且与轴交于
两点,如图所示,若,且的面积是
,求这对“M”函数的解析式;
(3)在(2)的条件下,若点是轴上的一个动点,当为等腰三角形时,请求出点的坐标.
25.(10分)观察图形,完成下列问题:
【动手证明】(1)如图1:四边形的两条对角线,交于点,若,
求证:;
【尝试应用】(2)如图2,在中,,,,分别以,为边向外作两个等腰直角三角形和,使得,连接,试求的长;
【拓展提高】(3)如图3,四边形是菱形,对角线,交于点,点,分别是,的中点,连接,并延长交于点,若,试求菱形的周长.
明德教育集团八年级期末考试
八年级数学试卷答案20-21学年第二学期
一、选择题(在下列各题的四个选项中,只有一项是符合题意的,请在答题卡中填涂符合题意的选项,本题共10题,每小题3分,共30分)
题次
1
2
3
4
5
6
7
8
9
10
答案
D
C
D
A
D
C
B
A
B
C
填空题(本题共6小题,每小题3分,共18分)
12.甲
14.
16.
三、解答题(共9个小题,第17,18,19题每小题6分,第20,21题每小题8分,第22,23题每小题9分,第24,25题每小题10分,共72分,解答应写出必要的文字说明或演算过程)
17.(6分)解:原式=3+2-2+1
----------------------4分
=4
----------------------6分
(6分)
解:(1)
--------------------------------3分
(2)
--------------------------------6分
(6分)(1)
----------------------3分
(2)
----------------------6分
20.(8分)解:(1).
---------------------------------------2分
(2)120人,图略.
-----------------------------------------4分
(3)甲、乙票数最多.
-
-------------------------------8分
21.(8分)解:(1)由题可知
OA=,图略.
--------------------------------6分
(2)当=5时,
----------
------------------8分
22.(9分)(1)证明:
------------------4分
(2)
-----------------------9分
(9分)解:(1)设
,依题意可得:
???
----------------------------4分
(2)设此设备的销售单价为万元/台,则每台设备的利润为
万元,销售数量为
台,根据题意得:
整理得:
,解得:
-------------------------9分
(10分)(1)解:根据题意,“M”函数为关于
轴对称的两个函数,
∴原函数的“M函数”为
--------------------3分
解:根据题意,
和
为一对“M函数”.
∴
,即
为等腰直角三角形,
即
,
∴
,
又∵
且
,
∴解得
,
那么
和
------------6分
解:根据等腰三角形的性质,分情况,
∵
,
,
∴以
为顶点,则
,得
,
,
以
为顶点,则
,得
,
以
为顶点,则
,得
-------------10分
25.(10分)(1)证明:,
,
,,,,
,,
.
-----------------------3分
(2)解:连接、交于点,交于,如图2所示:
和是等腰直角三角形,
,,,
,
即,
,
,
,,
,
,
,
由(1)得:,
在中,,
,
在中,,
,
,
解得:;
------------------------------6分
(3)解:连接,如图3所示:
四边形是菱形,
,,,
点,分别是,的中点,
是的中位线,
,,
是的中位线,
,,
在四边形中,,
,
即,
,
,
,
,
菱形的周长.
------------------------------10分
第
7
页
共
8
页
八年级
数学试卷
20-21学年第二学期
时量:120分钟
满分:120
分
一、选择题(在下列各题的四个选项中,只有一项是符合题意的,请在答题卡中填涂符合题意的选项,本题共10题,每小题3分,共30分)
1.如图,下列的四个图象中,不能表示是的函数图象的是(
).
A.
B.
C.
D.
2.下列运算结果正确的是(
)
A.
B.
C.
D.
3.下列各组数中,不能构成直角三角形的一组是
(
)
A.7,24,25
B.,4,5
C.3,4,5
D.4,5,6
4.在□ABCD中,如果,那么的大小是(
)
A.70°
B.75°
C.40°
D.20°
5.为了向建党一百周年献礼,我市中小学生开展了图说党史比赛.某参赛小组名同学的成绩(单位:分)分别为:关于这组数据,下列说法错误的是(
)
A.众数是
B.中位数是
C.平均数是
D.方差是
6.正方形具有而菱形不具有的性质是(
)
A.对角相等
B.对角线互相平分
C.对角线相等
D.对角线互相垂直
7.如图,在中,,分别以点A和点为圆心,以大于长为半径画弧,两弧交于点和点,作直线交于点,交于点,连接,则长为( )
A.3
B.2.5
C.2
D.1.5
8.对于一元二次方程,则它根的情况为(
)
A.没有实数根
B.两根之和是
C.两根之积是
D.有两个不相等的实数根
9.如图,直线和直线相交于点,则关于的不等式的解集为(
)
A.
B.
C.
D.
10.如图,在矩形中,,点在边上,连接,若平分,则的长为(
)
A.
B.
C.
D.
二、填空题(本题共6小题,每小题3分,共18分)
11.式子在实数范围内有意义,则实数的取值范围是
.
12.甲、乙两射击运动员10次射击训练的平均成绩恰好都是8.5环,方差分别是
则在本次测试中,
运动员的成绩更稳定(填“甲”或“乙”).
13.若直线上有两点和,则
(填
“>”或“<”).
14.已知关于的一元二次方程有一个根为,则另一个根是
.
15.如图,在菱形中,点分别是边、的中点,若,则长为
.
16.如图,在□ABCD中,将沿着所在的直线翻折得到,交于点,连接,若,则的长是
_.
三、解答题(共9个小题,第17,18,19题每小题6分,第20,21题每小题8分,第22,23题每小题9分,第24,25题每小题10分,共72分,解答应写出必要的文字说明或演算过程)
17.(6分)计算:
18.(6分)在四边形中,已知且于点.
试求:
(1)的长;
(2)的度数.
19.(6分)解一元二次方程:
(1)
(2)
20.(
8分)某校要选举一名学生会主席,先对甲、乙、丙三名候选人进行了笔试和面试,成绩如下表,又进行了学生投票,每个学生都投了一张票,且选票上只写了三名候选人中的一名,每张选票记0.5分,对选票进行统计后,绘有如图1,图2尚不完整的统计图.
请完成下列问题;
(1)乙的得票率是
,选票的总数为
__;
(2)补全图2的条形统计图;
(3)根据实际情况,学校选取票数最多的两位学生,从笔试、面试、学生投票三项得分按2∶4∶4的比例确定每人最终成绩,高者当选,请通过计算说明,哪位候选人当选?
(8分)点在第一象限,且,点的坐标为,设的面积为.
用含的式子表示,写出的取值范围,画出函数的图象;
当点的横坐标为时,的面积是多少?
22.(9分)如图,□ABCD的对角线,相交于点,是等边三角形,.
(1)求证:□ABCD是矩形;
(2)求点到线段的距离.
23.(9分)为了积极响应新旧功能转换,提高公司的经济效益,某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为35万元时,年销售量为550台;每台售价为40万元时,年销售量为500台,假定该设备的年销售量(单位:台)和销售单价(单位:万元)成一次函数关系.
求年销售量与销售单价的函数关系式;
根据相关规定,此设备的销售单价不得高于60万元,如果该公司想获得8000万元的年利润,则该设备的销售单价应为多少万元?
24.(10分)我们知道一次函数
与
的图象关于轴对称,所以我们定义:函数
与
互为“M”函数.
(1)请直接写出函数
的“M”函数;
(2)如果一对“M”函数
与
的图象交于点,且与轴交于
两点,如图所示,若,且的面积是
,求这对“M”函数的解析式;
(3)在(2)的条件下,若点是轴上的一个动点,当为等腰三角形时,请求出点的坐标.
25.(10分)观察图形,完成下列问题:
【动手证明】(1)如图1:四边形的两条对角线,交于点,若,
求证:;
【尝试应用】(2)如图2,在中,,,,分别以,为边向外作两个等腰直角三角形和,使得,连接,试求的长;
【拓展提高】(3)如图3,四边形是菱形,对角线,交于点,点,分别是,的中点,连接,并延长交于点,若,试求菱形的周长.
明德教育集团八年级期末考试
八年级数学试卷答案20-21学年第二学期
一、选择题(在下列各题的四个选项中,只有一项是符合题意的,请在答题卡中填涂符合题意的选项,本题共10题,每小题3分,共30分)
题次
1
2
3
4
5
6
7
8
9
10
答案
D
C
D
A
D
C
B
A
B
C
填空题(本题共6小题,每小题3分,共18分)
12.甲
14.
16.
三、解答题(共9个小题,第17,18,19题每小题6分,第20,21题每小题8分,第22,23题每小题9分,第24,25题每小题10分,共72分,解答应写出必要的文字说明或演算过程)
17.(6分)解:原式=3+2-2+1
----------------------4分
=4
----------------------6分
(6分)
解:(1)
--------------------------------3分
(2)
--------------------------------6分
(6分)(1)
----------------------3分
(2)
----------------------6分
20.(8分)解:(1).
---------------------------------------2分
(2)120人,图略.
-----------------------------------------4分
(3)甲、乙票数最多.
-
-------------------------------8分
21.(8分)解:(1)由题可知
OA=,图略.
--------------------------------6分
(2)当=5时,
----------
------------------8分
22.(9分)(1)证明:
------------------4分
(2)
-----------------------9分
(9分)解:(1)设
,依题意可得:
???
----------------------------4分
(2)设此设备的销售单价为万元/台,则每台设备的利润为
万元,销售数量为
台,根据题意得:
整理得:
,解得:
-------------------------9分
(10分)(1)解:根据题意,“M”函数为关于
轴对称的两个函数,
∴原函数的“M函数”为
--------------------3分
解:根据题意,
和
为一对“M函数”.
∴
,即
为等腰直角三角形,
即
,
∴
,
又∵
且
,
∴解得
,
那么
和
------------6分
解:根据等腰三角形的性质,分情况,
∵
,
,
∴以
为顶点,则
,得
,
,
以
为顶点,则
,得
,
以
为顶点,则
,得
-------------10分
25.(10分)(1)证明:,
,
,,,,
,,
.
-----------------------3分
(2)解:连接、交于点,交于,如图2所示:
和是等腰直角三角形,
,,,
,
即,
,
,
,,
,
,
,
由(1)得:,
在中,,
,
在中,,
,
,
解得:;
------------------------------6分
(3)解:连接,如图3所示:
四边形是菱形,
,,,
点,分别是,的中点,
是的中位线,
,,
是的中位线,
,,
在四边形中,,
,
即,
,
,
,
,
菱形的周长.
------------------------------10分
第
7
页
共
8
页
同课章节目录
