黑龙江省哈尔滨市木兰高级中学2011-2012学年高一物理课件:5.2 质点在平面内的运动
文档属性
| 名称 | 黑龙江省哈尔滨市木兰高级中学2011-2012学年高一物理课件:5.2 质点在平面内的运动 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2012-04-27 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
第六章 曲线运动
2、质点在平面内的运动
v0
回顾
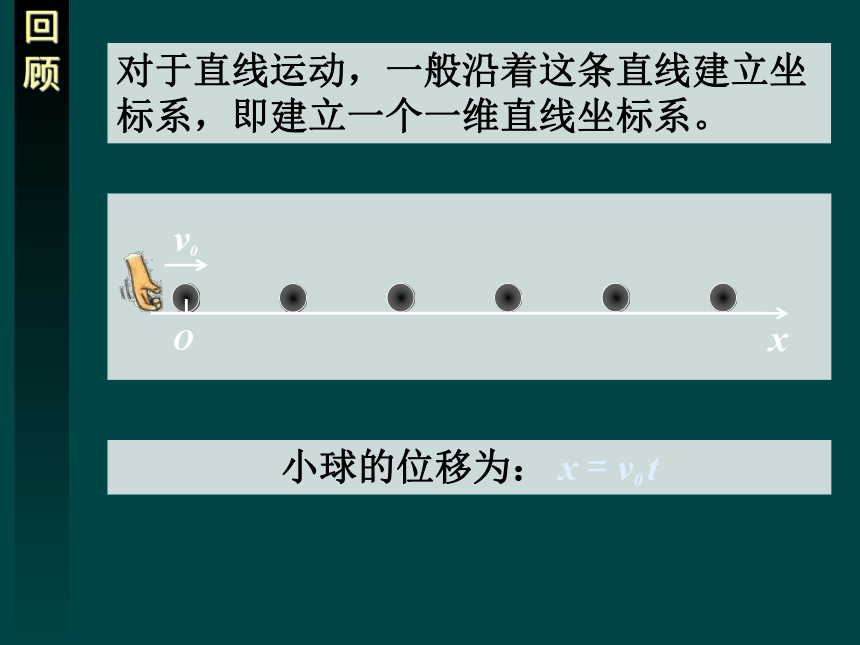
对于直线运动,一般沿着这条直线建立坐标系,即建立一个一维直线坐标系。
小球的位移为: x = v0 t
O
x
回顾
对于直线运动,一般沿着这条直线建立坐标系,即建立一个一维直线坐标系。
O
y
小球的位移为: y = a t 2
1
2
思考
如果物体运动的轨迹不是直线而是曲线,怎样研究、描述这样的曲线运动呢?
建立平面直角坐标系
蜡块的运动
思考:蜡块的实际运动的轨迹是直线吗?实际运动是匀速运动吗?
蜡块既向上做匀速运动,又由于玻璃管的移动向右做匀速运动,即蜡块是向右上方运动的。
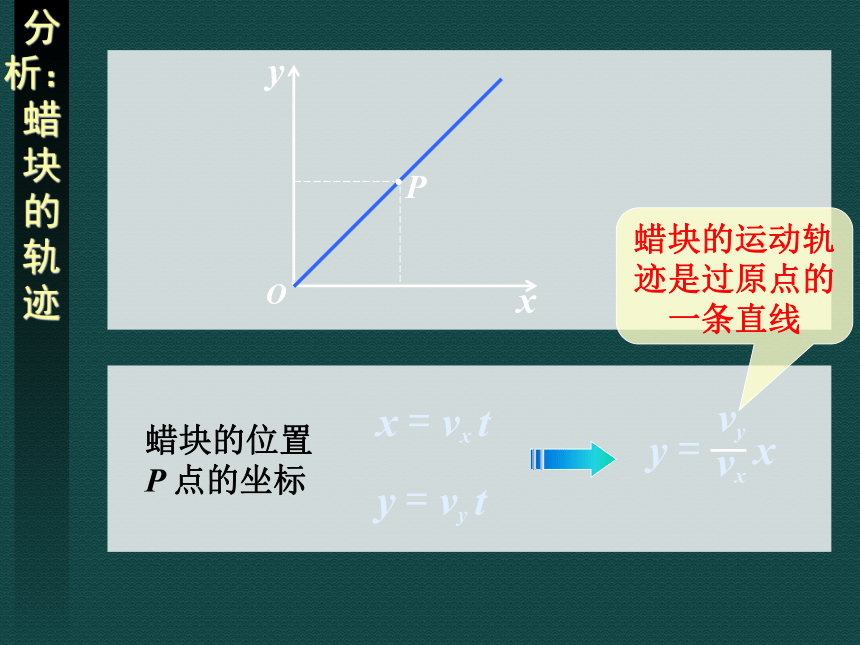
分析:蜡块的轨迹
O
x
y
P
蜡块的位置P 点的坐标
y = x
vx
vy
蜡块的运动轨迹是过原点的一条直线
y = vy t
x = vx t
O
x
y
P
θ
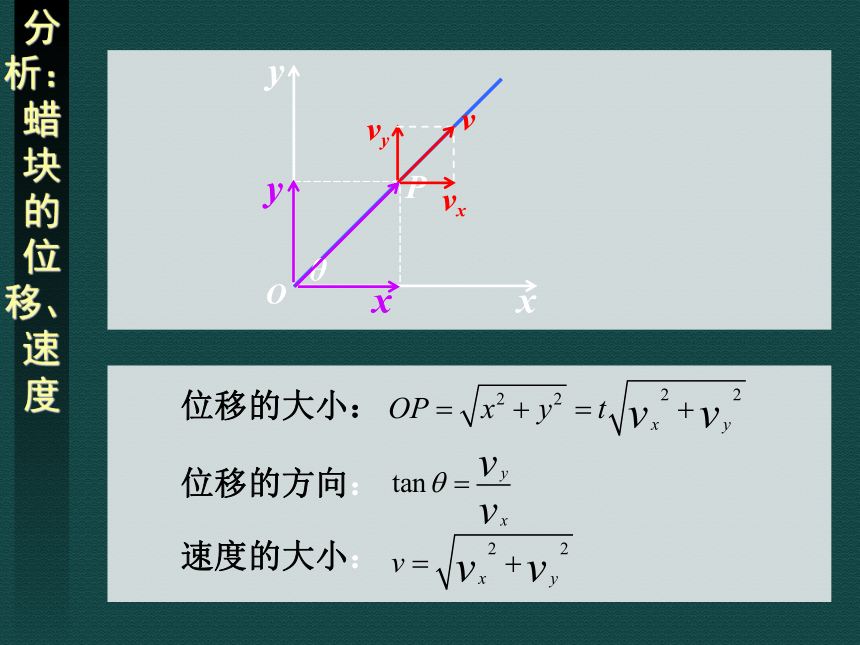
分析:蜡块的位移、速度
vy
vx
v
y
x
位移的大小:
位移的方向:
速度的大小:
运动的合成与分解
1、物体实际的运动叫合运动
2、物体同时参与合成的运动的运动叫分运动
3、由分运动求合运动的过程叫运动的合成
4、由合运动求分运动的过程叫运动的分解
说明
1、运动的独立性
2、运动的等时性
3、运动的等效性
4、运动的同体性
a
a1
a2
v1
v2
v
运动的合成与分解
运动的合成与分解是指 x 、v、 a 的合成与分解。
速度、位移、加速度都是矢量,合成时均遵循平行四边形定则
A
B
x
x1
x2
分速度
分速度
合速度
分加速度
合加速度
位移的合成
速度的合成
加速度的合成
分加速度
合位移
分位移
分位移
运动的合成是惟一的,而运动的分解不是惟一的,通常按运动所产生的实际效果分解。
课本例题
飞机起飞时以 300km/h 的速度斜向上飞,飞行方向与水平方面的夹角30°。求水平方向的分速度vx和竖直方向的分速度vy 。
v
vy
vx
30°
vy= v sin30°
vx= v cos30°
思考与讨论
如果物体在一个方向上的分运动是匀速直线运动,在与它垂直方向的分运动是匀加速运动,合运动的轨迹是什么样的?
P
x = vx t
物体的位置P 的坐标
y = vy t+ at2
1
2
y = x+ x2
vx
vy
2vx2
a
v
x
y
O
F合
vy
vx
结论
1、两个互成角度的匀速直线运动的合运动
匀速直线运动
2、两个互成角度的匀速直线运动与匀变速直线运动的合运动
匀变速曲线运动
a1
v1
a1
v1
思考与讨论
3、两个互成角度的匀变速直线运动的合运动
①两个初速度为0 的匀加速直线运动
判断几个分运动的合运动,可先把各分运动的合速度以及合加速度求出来,然后根据合速度与合加速度是否在一条直线上加以判断。
②两个初速度不为0 的匀变速直线运动
初速度为0的匀加速直线运动
匀变速直线运动
a2
v2
v
a2
v2
v
a
匀变速曲线运动
a
练习
关于运动的合成,下列说法中正确的是
A、合运动的速度一定比每一个分运动的速度大
B、两个速度不等的匀速直线运动的合运动,一定是匀速直线运动
C、两个分运动是直线运动的合运动,一定是直线运动
D、两个分运动的时间,一定与它们的合运动的时间相等
B D
小结
1、合运动与分运动的概念
3、运动的合成与分解遵循平行四边形定则
4、两个直线运动的合运动可能是直线运动,也可能是曲线运动
2、合运动与分运动的关系:独立性、等时性、等效性、同体性
第六章 曲线运动
2、质点在平面内的运动
v0
回顾
对于直线运动,一般沿着这条直线建立坐标系,即建立一个一维直线坐标系。
小球的位移为: x = v0 t
O
x
回顾
对于直线运动,一般沿着这条直线建立坐标系,即建立一个一维直线坐标系。
O
y
小球的位移为: y = a t 2
1
2
思考
如果物体运动的轨迹不是直线而是曲线,怎样研究、描述这样的曲线运动呢?
建立平面直角坐标系
蜡块的运动
思考:蜡块的实际运动的轨迹是直线吗?实际运动是匀速运动吗?
蜡块既向上做匀速运动,又由于玻璃管的移动向右做匀速运动,即蜡块是向右上方运动的。
分析:蜡块的轨迹
O
x
y
P
蜡块的位置P 点的坐标
y = x
vx
vy
蜡块的运动轨迹是过原点的一条直线
y = vy t
x = vx t
O
x
y
P
θ
分析:蜡块的位移、速度
vy
vx
v
y
x
位移的大小:
位移的方向:
速度的大小:
运动的合成与分解
1、物体实际的运动叫合运动
2、物体同时参与合成的运动的运动叫分运动
3、由分运动求合运动的过程叫运动的合成
4、由合运动求分运动的过程叫运动的分解
说明
1、运动的独立性
2、运动的等时性
3、运动的等效性
4、运动的同体性
a
a1
a2
v1
v2
v
运动的合成与分解
运动的合成与分解是指 x 、v、 a 的合成与分解。
速度、位移、加速度都是矢量,合成时均遵循平行四边形定则
A
B
x
x1
x2
分速度
分速度
合速度
分加速度
合加速度
位移的合成
速度的合成
加速度的合成
分加速度
合位移
分位移
分位移
运动的合成是惟一的,而运动的分解不是惟一的,通常按运动所产生的实际效果分解。
课本例题
飞机起飞时以 300km/h 的速度斜向上飞,飞行方向与水平方面的夹角30°。求水平方向的分速度vx和竖直方向的分速度vy 。
v
vy
vx
30°
vy= v sin30°
vx= v cos30°
思考与讨论
如果物体在一个方向上的分运动是匀速直线运动,在与它垂直方向的分运动是匀加速运动,合运动的轨迹是什么样的?
P
x = vx t
物体的位置P 的坐标
y = vy t+ at2
1
2
y = x+ x2
vx
vy
2vx2
a
v
x
y
O
F合
vy
vx
结论
1、两个互成角度的匀速直线运动的合运动
匀速直线运动
2、两个互成角度的匀速直线运动与匀变速直线运动的合运动
匀变速曲线运动
a1
v1
a1
v1
思考与讨论
3、两个互成角度的匀变速直线运动的合运动
①两个初速度为0 的匀加速直线运动
判断几个分运动的合运动,可先把各分运动的合速度以及合加速度求出来,然后根据合速度与合加速度是否在一条直线上加以判断。
②两个初速度不为0 的匀变速直线运动
初速度为0的匀加速直线运动
匀变速直线运动
a2
v2
v
a2
v2
v
a
匀变速曲线运动
a
练习
关于运动的合成,下列说法中正确的是
A、合运动的速度一定比每一个分运动的速度大
B、两个速度不等的匀速直线运动的合运动,一定是匀速直线运动
C、两个分运动是直线运动的合运动,一定是直线运动
D、两个分运动的时间,一定与它们的合运动的时间相等
B D
小结
1、合运动与分运动的概念
3、运动的合成与分解遵循平行四边形定则
4、两个直线运动的合运动可能是直线运动,也可能是曲线运动
2、合运动与分运动的关系:独立性、等时性、等效性、同体性
