山东省潍坊市2011-2012学年度第二学期期中质量检测八年级数学试题(带答案)
文档属性
| 名称 | 山东省潍坊市2011-2012学年度第二学期期中质量检测八年级数学试题(带答案) |  | |
| 格式 | zip | ||
| 文件大小 | 287.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-03 10:33:00 | ||
图片预览




文档简介
2011-2012学年度第二学期期中质量检测
八年级数学试题
(时间120分钟)
注意事项:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.
2.答卷前,考生务必将自己的姓名、准考证号填写在试题卷上.
3.选择题每小题选出答案后,将正确答案填写在第Ⅱ卷的表格里,答在原题上无效.
4.填空题和解答题答案用黑色或蓝色墨水钢笔在相应位置书写.
第I卷 选择题
一、选择题:本大题共10小题,在每小题给出的四个选项中,只有一项是符合题目要求的,将正确选项的代号填写在答题纸的表格中.
1. 下列各式中,计算正确的是
A、 B、
C、 D、
2. 下列结论正确的是
A、所有正五边形都相似 B、所有平行四边形都相似
C、所有菱形都相似 D、所有长方形都相似
3. 在Rt△中,,,则的度数为
A、 B、 C、 D、
4. 如图,已知,是垂足,,下列判断:①△≌△; ②△与△不全等;
③; ④;
⑤平分.其中正确的是
A、①③④ B、②③④⑤ C、①③④⑤ D、③⑤
5. 如图,小正方形边长均为1,则下列图形中三角形(阴影部分)与△ABC相似的是
6. 化简二次根式(),得
A、 B、 C、 D、
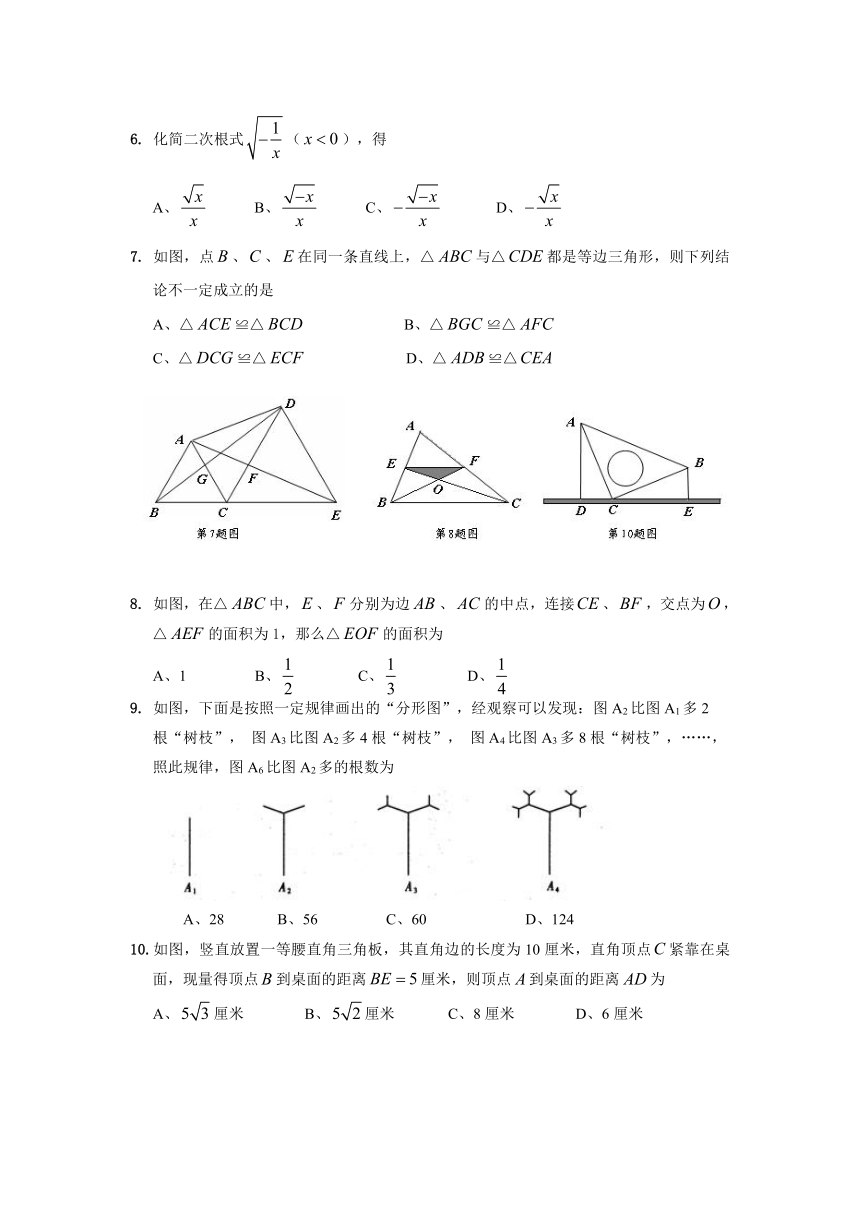
7. 如图,点、、在同一条直线上,△与△都是等边三角形,则下列结论不一定成立的是
A、△≌△ B、△≌△
C、△≌△ D、△≌△
8. 如图,在△中,、分别为边、的中点,连接、,交点为,△的面积为1,那么△的面积为
A、1 B、 C、 D、
9. 如图,下面是按照一定规律画出的“分形图”,经观察可以发现:图A2比图A1多2
根“树枝”, 图A3比图A2多4根“树枝”, 图A4比图A3多8根“树枝”,……,
照此规律,图A6比图A2多的根数为
A、28 B、56 C、60 D、124
10.如图,竖直放置一等腰直角三角板,其直角边的长度为10厘米,直角顶点紧靠在桌面,现量得顶点到桌面的距离厘米,则顶点到桌面的距离为
A、厘米 B、厘米 C、8厘米 D、6厘米
2011-2012学年度第二学期期中质量检测
八年级数学试题
题号 一 二 三 总分
19 20 21 22 23 24
得分
阅卷人
第Ⅱ卷 非选择题
一、选择题答题表:
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题:本大题共8小题,把答案填写在相应的横线上.
11. 将化成最简二次根式为______________.
12. 如图,胶州湾大桥是一座斜拉式大桥,斜拉式大桥多采用三角形结构,使其不易变形,这种做法的依据是______________.
13. 如图,小亮欲测量一建筑物的高度. 他站在该建筑物的影子上,前后移动,直到他本身影子的顶端正好与建筑物影子的顶端重叠. 此时,他距离该建筑物18米. 小亮的身高是1.6米,他的影子长是2米,那么该建筑物的高度是______________.
14. 如图所示,正方形中,点在上,点在上,请添加一个条件: ,使△≌△(只添一个条件即可).
15. 在Rt△中,,,那么______________.
16. 如图,、为、的中点,将△沿线段折叠,使点落在点处,若∠=55°,则∠=_____________.
17. 如图,质地均匀的空心圆柱形零件的外直径为,现用一个交叉钳(和的长相等)测量,如果,而且,那么这个零件的厚度为__________________.
18. 由,得;
由,得;
……
观察上面的规律,写出你的发现____________________. (用含的式子表示)
三、解答题:本大题共6小题,解答应写出必要的计算过程、推演步骤或文字说明.
19.计算题:
(1) (2)
(3)
20. 如图,线段∥,=,连接,、是上的两点,且∥.
(1)求证:△≌△;
(2)若,且,,求的长.
21. 如图,线段与交于点,且,,,.
(1)图1,△与△相似吗?如果相似,请予以证明;如果不相似,说明理由;
(2)图2,作∥,求△与△的面积之比.
22. 由于全球气候变暖,导致一些冰川融化消失.在冰川消失12年后,一种低等植物苔藓就开始在岩石上丛生.每一丛苔藓都会近似长成圆形,毎丛苔藓的直径(单位:厘米)与冰川消失之后经过的时间(单位:年)近似地满足关系式.
(1)求关系中的取值范围;
(2)计算冰川消失21年后,一丛苔藓的直径;
(3)如果测得一丛苔藓的直径是42厘米,那么冰川大约是在多少年前消失的?
23. 如图,在△中,,点在上,,,. 求:
(1)的长;
(2)的值.
24. 如图,在直角三角形中,∠=90°,点在线段上,∠=∠,,垂足为,与相交于点.
(1)当时(如图1),作∥,交于,交延长线于点.
①∠=_______°;
②通过证明△≌△与△≌△,可得,请说明这一推理过程.
(2)当时(如图2),证明:.
2011-2012学年度第二学期期中质量检测
八年级数学试题答案及评分标准
一、选择题:本大题共10小题,每小题3分,共30分
题号 1 2 3 4 5 6 7 8 9 10
答案 D A B C B C D C C A
二、填空题:本大题共8小题,每小题3分,共24分.
11.,12.三角形的稳定性,13.16米,14.(答案不唯一),15.,
16.,17.,18.
三、解答题:本大题共6小题,共66分.
19.(每题4分,满分12分)解:(1);(2);(3)5.
20.(满分10分)解:(1)∵,∥
∴.又∵∥, ∴.……………2分
()
()
∴()
∴△≌△(ASA)(AAS). ……………6分
(2).……………10分
21.(满分10分)证明:(1)相似.∵,,,.
∴,,又,
∴△∽△.……………5分
(2)∵∥,∴,又,
∴△∽△. ∴.……10分
22.(每问4分,满分12分)解:(1)≥12;(2)21;(3)48.
23.(满分10分)解:(1)设,在△中,∵,
∴,即.∴,解得,.…………5分
(2)由(1)知,,∴.
在△中,,
∴.……………10分
24.(满分12分)解:(1)①22.5;②证明如下:
∵∥,∠=∠,∴∠=∠.
又∵⊥,∴∠=∠=90°.
又∵,∴△≌△(AAS).
∴,即.……………4分
∵∥,∠A=90°,,∴∠=∠=90°,.
又∵,∴△≌△(AAS).∴.
∴.……………7分
(2)作∥,交于,交延长线于点.
同(1)可证.∵∥,
∴,
又∵,∴△∽△,∴
∵∥,∴△∽△,∴.…………10分
∴,即,.……………12分
八年级数学试题
(时间120分钟)
注意事项:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.
2.答卷前,考生务必将自己的姓名、准考证号填写在试题卷上.
3.选择题每小题选出答案后,将正确答案填写在第Ⅱ卷的表格里,答在原题上无效.
4.填空题和解答题答案用黑色或蓝色墨水钢笔在相应位置书写.
第I卷 选择题
一、选择题:本大题共10小题,在每小题给出的四个选项中,只有一项是符合题目要求的,将正确选项的代号填写在答题纸的表格中.
1. 下列各式中,计算正确的是
A、 B、
C、 D、
2. 下列结论正确的是
A、所有正五边形都相似 B、所有平行四边形都相似
C、所有菱形都相似 D、所有长方形都相似
3. 在Rt△中,,,则的度数为
A、 B、 C、 D、
4. 如图,已知,是垂足,,下列判断:①△≌△; ②△与△不全等;
③; ④;
⑤平分.其中正确的是
A、①③④ B、②③④⑤ C、①③④⑤ D、③⑤
5. 如图,小正方形边长均为1,则下列图形中三角形(阴影部分)与△ABC相似的是
6. 化简二次根式(),得
A、 B、 C、 D、
7. 如图,点、、在同一条直线上,△与△都是等边三角形,则下列结论不一定成立的是
A、△≌△ B、△≌△
C、△≌△ D、△≌△
8. 如图,在△中,、分别为边、的中点,连接、,交点为,△的面积为1,那么△的面积为
A、1 B、 C、 D、
9. 如图,下面是按照一定规律画出的“分形图”,经观察可以发现:图A2比图A1多2
根“树枝”, 图A3比图A2多4根“树枝”, 图A4比图A3多8根“树枝”,……,
照此规律,图A6比图A2多的根数为
A、28 B、56 C、60 D、124
10.如图,竖直放置一等腰直角三角板,其直角边的长度为10厘米,直角顶点紧靠在桌面,现量得顶点到桌面的距离厘米,则顶点到桌面的距离为
A、厘米 B、厘米 C、8厘米 D、6厘米
2011-2012学年度第二学期期中质量检测
八年级数学试题
题号 一 二 三 总分
19 20 21 22 23 24
得分
阅卷人
第Ⅱ卷 非选择题
一、选择题答题表:
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题:本大题共8小题,把答案填写在相应的横线上.
11. 将化成最简二次根式为______________.
12. 如图,胶州湾大桥是一座斜拉式大桥,斜拉式大桥多采用三角形结构,使其不易变形,这种做法的依据是______________.
13. 如图,小亮欲测量一建筑物的高度. 他站在该建筑物的影子上,前后移动,直到他本身影子的顶端正好与建筑物影子的顶端重叠. 此时,他距离该建筑物18米. 小亮的身高是1.6米,他的影子长是2米,那么该建筑物的高度是______________.
14. 如图所示,正方形中,点在上,点在上,请添加一个条件: ,使△≌△(只添一个条件即可).
15. 在Rt△中,,,那么______________.
16. 如图,、为、的中点,将△沿线段折叠,使点落在点处,若∠=55°,则∠=_____________.
17. 如图,质地均匀的空心圆柱形零件的外直径为,现用一个交叉钳(和的长相等)测量,如果,而且,那么这个零件的厚度为__________________.
18. 由,得;
由,得;
……
观察上面的规律,写出你的发现____________________. (用含的式子表示)
三、解答题:本大题共6小题,解答应写出必要的计算过程、推演步骤或文字说明.
19.计算题:
(1) (2)
(3)
20. 如图,线段∥,=,连接,、是上的两点,且∥.
(1)求证:△≌△;
(2)若,且,,求的长.
21. 如图,线段与交于点,且,,,.
(1)图1,△与△相似吗?如果相似,请予以证明;如果不相似,说明理由;
(2)图2,作∥,求△与△的面积之比.
22. 由于全球气候变暖,导致一些冰川融化消失.在冰川消失12年后,一种低等植物苔藓就开始在岩石上丛生.每一丛苔藓都会近似长成圆形,毎丛苔藓的直径(单位:厘米)与冰川消失之后经过的时间(单位:年)近似地满足关系式.
(1)求关系中的取值范围;
(2)计算冰川消失21年后,一丛苔藓的直径;
(3)如果测得一丛苔藓的直径是42厘米,那么冰川大约是在多少年前消失的?
23. 如图,在△中,,点在上,,,. 求:
(1)的长;
(2)的值.
24. 如图,在直角三角形中,∠=90°,点在线段上,∠=∠,,垂足为,与相交于点.
(1)当时(如图1),作∥,交于,交延长线于点.
①∠=_______°;
②通过证明△≌△与△≌△,可得,请说明这一推理过程.
(2)当时(如图2),证明:.
2011-2012学年度第二学期期中质量检测
八年级数学试题答案及评分标准
一、选择题:本大题共10小题,每小题3分,共30分
题号 1 2 3 4 5 6 7 8 9 10
答案 D A B C B C D C C A
二、填空题:本大题共8小题,每小题3分,共24分.
11.,12.三角形的稳定性,13.16米,14.(答案不唯一),15.,
16.,17.,18.
三、解答题:本大题共6小题,共66分.
19.(每题4分,满分12分)解:(1);(2);(3)5.
20.(满分10分)解:(1)∵,∥
∴.又∵∥, ∴.……………2分
()
()
∴()
∴△≌△(ASA)(AAS). ……………6分
(2).……………10分
21.(满分10分)证明:(1)相似.∵,,,.
∴,,又,
∴△∽△.……………5分
(2)∵∥,∴,又,
∴△∽△. ∴.……10分
22.(每问4分,满分12分)解:(1)≥12;(2)21;(3)48.
23.(满分10分)解:(1)设,在△中,∵,
∴,即.∴,解得,.…………5分
(2)由(1)知,,∴.
在△中,,
∴.……………10分
24.(满分12分)解:(1)①22.5;②证明如下:
∵∥,∠=∠,∴∠=∠.
又∵⊥,∴∠=∠=90°.
又∵,∴△≌△(AAS).
∴,即.……………4分
∵∥,∠A=90°,,∴∠=∠=90°,.
又∵,∴△≌△(AAS).∴.
∴.……………7分
(2)作∥,交于,交延长线于点.
同(1)可证.∵∥,
∴,
又∵,∴△∽△,∴
∵∥,∴△∽△,∴.…………10分
∴,即,.……………12分
同课章节目录
