11.2.1 三角形的内角 课时达标检测(含解析)
文档属性
| 名称 | 11.2.1 三角形的内角 课时达标检测(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-08 14:26:38 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版2021年八年级上册数学同步练习卷
11.2与三角形有关的角
11.2.1 三角形的内角
一、单选题
1.如果三角形的两个内角都小于,那么这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
2.如图,直线,三角尺的直角顶点在直线m上,且三角尺的直角被直线m平分,若,则下列结论错误的是( )
A. B. C. D.
3.如图,已知直线AB∥CD,直线AC和BD相交于点E,若∠ABE=75°,∠ACD=35°,则∠AEB等于( )
A.60° B.70° C.75° D.80°
4.如图,直线,点、在上,射线交于点,平分交于点,若,则的度数是( )
A. B. C. D.
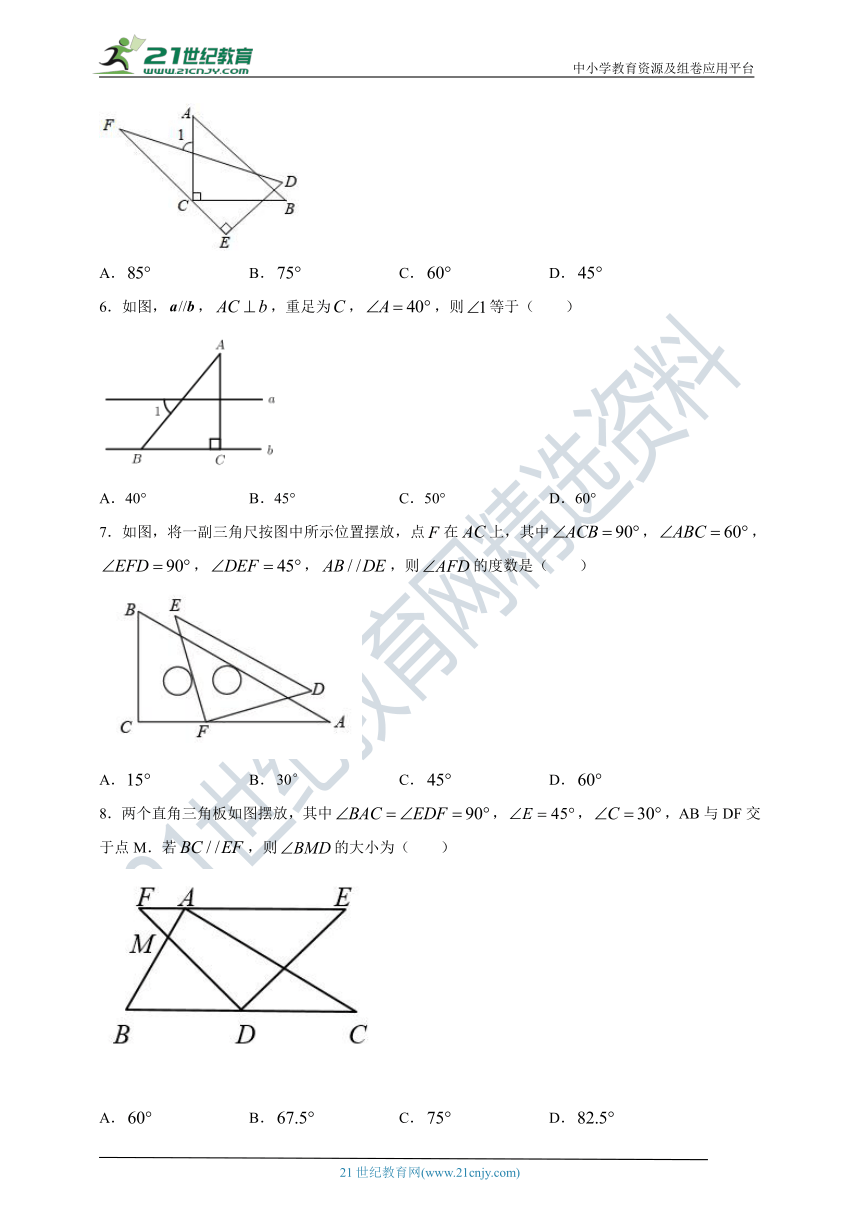
5.将一副直角三角板按如图放置(其中),使含角的三角板的较长直角边与等腰直角三角板的斜边平行,则图中的度数为( )
A. B. C. D.
6.如图,,,重足为,,则等于( )
A.40° B.45° C.50° D.60°
7.如图,将一副三角尺按图中所示位置摆放,点在上,其中,,,,,则的度数是( )
A. B. C. D.
8.两个直角三角板如图摆放,其中,,,AB与DF交于点M.若,则的大小为( )
A. B. C. D.
9.如图,平分交于点E,,,M,N分别是延长线上的点,和的平分线交于点F.下列结论:①;②;③平分;④为定值.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
10.如图,在中,是的平分线,是外角的平分线,与相交于点,若,则是( )
A. B. C. D.
11.若△ABC内有一个点P1,当P1、A、B、C没有任何三点在同一直线上时,如图1,可构成3个互不重叠的小三角形;若△ABC内有两个点P1、P2,其它条件不变,如图2,可构成5个互不重叠的小三角形:……若△ABC内有n个点,其它条件不变,则构成若干个互不重叠的小三角形,这些小三角形的内角和为()
A.n·180° B.(n+2)·180° C.(2n-1)·180° D.(2n+1)·180°
12.如图所示,在四边形纸片ABCD中,∠A=80°,∠B=70°,将纸片沿着MN折叠,使C,D分别落在直线AB上的,处,则∠+∠等于( )
A.50° B.60° C.70° D.80°
二、填空题
13.在中,,,则的度数是______.
14.一个三角形三个内角的比是,它的面积是12,则它的周长是______.
15.如图,平面直角坐标系中的两个点,过C作轴于B,过B作交y轴于D,且,分别平分,,则的度数为______________________.
16.如图,把沿线段折叠,使点A落在点F处,,若,则__.
17.如图,△ABC中,∠BDC=90°,BE、CE分别平分∠ABD和∠ACD,BF、CF分别平分∠ABE和∠ACE,若∠A=40°,则∠F=__°.
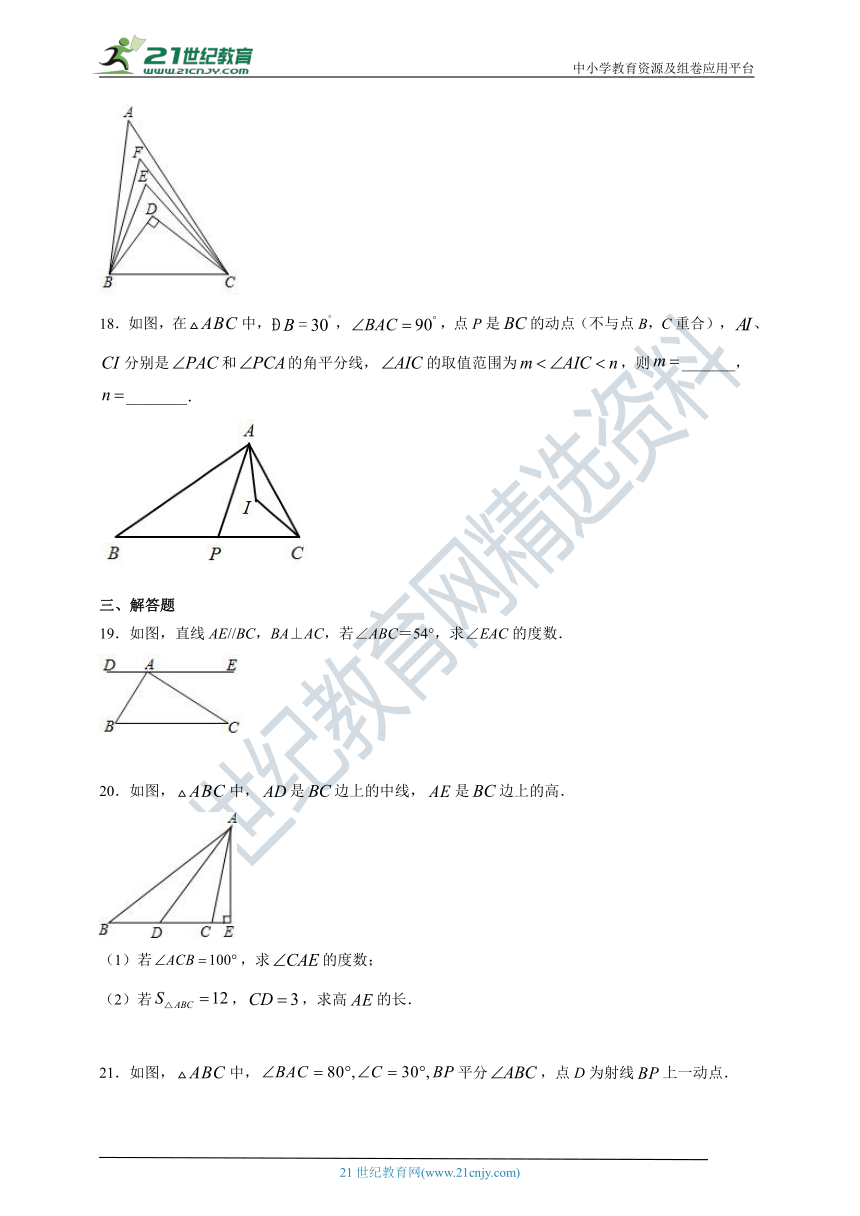
18.如图,在中,,,点P是的动点(不与点B,C重合),、分别是和的角平分线,的取值范围为,则_______,________.
三、解答题
19.如图,直线AE//BC,BA⊥AC,若∠ABC=54°,求∠EAC的度数.
20.如图,中,是边上的中线,是边上的高.
(1)若,求的度数;
(2)若,,求高的长.
21.如图,中,平分,点D为射线上一动点.
(1)连接,若,求的度数;
(2)连接,若所在的直线垂直于的一边,则所有满足条件的的度数为__________.
22.已知,
(1)若,则________,
(2)如图1,分别平分,试说明.;
(3)如图2.若分别平分.求的度数.
23.如图1,含角的直角三角板与含角的直角三角板的斜边在同一直线上,D为的中点,将直角三角板绕点D按逆时针方向旋转,在旋转过程中:
(1)如图2,当________时,;当______时,;
(2)如图③,当直角三角板的边、分别交、的延长线于点M、N时;
①与度数的和是否变化?若不变,求出与度数的和;若变化,请说明理由;
②若使得,求出、的度数,并直接写出此时的度数;
③若使得,求的度数范围.
参考答案
1.C
【详解】
设中
是钝角三角形
故选C.
2.D
【详解】
首先根据三角尺的直角被直线m平分,
∴∠6=∠7=45°;
A、∵∠1=60°,∠6=45°,∴∠8=180°-∠1-∠6=180-60°-45°=75°,m∥n,∴∠2=∠8=75°结论正确,选项不合题意;
B、∵∠7=45°,m∥n,∴∠3=∠7=45°,结论正确,选项不合题意;
C、∵∠8=75°,∴∠4=180-∠8=180-75°=105°,结论正确,选项不合题意;
D、∵∠7=45°,∴∠5=180-∠7=180-45°=135°,结论错误,选项符合题意.
3.B
【详解】
解:∵AB∥CD,
∴∠BAE=∠ACD=35°.
∵∠AEB+∠BAE+∠ABE=180°,∠ABE=75°,
∴∠AEB=70°.
4.B
【详解】
解:如图,
∵,
∴∠3=∠1=80°
∴∠ABD=180°-80°=100°
∵平分
∴
又
∴
5.B
【详解】
解:如图:根据特殊直角三角形的性质可知,∠A=45°,∠F=30°,
∵AB∥EF,
∴∠ACF=∠A=45°,
∴∠CHF=180°-∠F-∠ACF=180°-30°-45°=105°,
∴∠1=180°-∠CHF=108°-105°=75°,
故选:B.
6.C
【详解】
解:∵,
∴∠ACB=90°,
∵,
∴∠ABC=90°-=50°,
∵
∴,
7.A
【详解】
解:设AB与EF交于点M,
∵,
∴,
∵,,
∴,
∴,
∵,
∴=,
8.C
【详解】
由图可得
∵,
∴
∴
9.C
【详解】
解:∵AB⊥BC,AE⊥DE,
∴∠1+∠AEB=90°,∠DEC+∠AEB=90°,
∴∠1=∠DEC,
又∵∠1+∠2=90°,
∴∠DEC+∠2=90°,
∴∠C=90°,
∴∠B+∠C=180°,
∴AB∥CD,故①正确;
∴∠ADN=∠BAD,
∵∠ADC+∠ADN=180°,
∴∠BAD+∠ADC=180°,
又∵∠AEB≠∠BAD,
∴AEB+∠ADC≠180°,故②错误;
∵∠4+∠3=90°,∠2+∠1=90°,而∠3=∠1,
∴∠2=∠4,
∴ED平分∠ADC,故③正确;
∵∠1+∠2=90°,
∴∠EAM+∠EDN=360°-90°=270°.
∵∠EAM和∠EDN的平分线交于点F,
∴∠EAF+∠EDF=×270°=135°.
∵AE⊥DE,
∴∠3+∠4=90°,
∴∠FAD+∠FDA=135°-90°=45°,
∴∠F=180°-(∠FAD+∠FDA)=180-45°=135°,故④正确.
10.C
【详解】
解:∵是的平分线,
∴∠ABC=2∠DBC,
同理,∠ACM=2∠DCM,
∵∠ACM=∠A+∠ABC,
∴2∠DCM=∠A+2∠DBC
∵∠DCM=∠D+∠DBC,
∴∠A=2∠D,
∵,
∴,
11.D
【详解】
图1中,当△ABC内只有1个点时,可分割成3个互不重叠的小三角形;
图2中,当△ABC内只有2个点时,可分割成5个互不重叠的小三角形;
图3中,当△ABC内只有3个点时,可分割成7个互不重叠的小三角形;
根据以上规律,当△ABC内有n个点(P1,P2,…,Pn)时,可以把△ABC分割成S=2n+1个互不重叠的三角形,所以这些小三角形的内角和为(2n+1)·180°.
12.B
【详解】
∵∠A=80°,∠B=70°,
∴∠D+∠C=360°?∠A?∠B=210°,
由折叠性质可得:∠=∠D,∠=∠C,
∴∠+∠=210°,
∴∠+∠=360°?(∠+∠)=150°,
∴∠+∠=360°?(∠+∠)?(∠A+∠B)=60°,
13.75°
【详解】
.
14.
【详解】
解:此三角形各角的度数分别是:
,
,
由此知三角形是等腰直角三角形;
设直角边为a,根据勾股定理可知斜边为,
∵,
即,
∴,
则斜边应是,
那么,
即,
故答案为:.
15.45°
【详解】
连接AD,如图所示:
∵BD∥AC,
∴∠BAC=∠ABD,
∵∠ABD+∠ODB=90°,
∴∠BAC+∠ODB=90°,
∵AE,DE分别平分∠CAB,∠ODB,
∴,
∴,
∵∠AED+∠EAD+∠EDA=180°,即∠AED+∠EAO+∠OAD+∠EDO+∠ODA=180°,
∵∠OAD+∠ODA=90°,
∴∠AED+45°+90°=180°,
∴∠AED=45°.
16.60
【详解】
解:∵BC∥DE,若∠B=60°,
∴∠ADE=60°,
又∵△ABC沿线段DE折叠,使点A落在点F处,
∴∠ADE=∠EDF=60°,
∴∠BDF=180°-60°-60°=60°,
17.52.5.
【详解】
解:∵∠A=40°,
∴∠ABC+∠ACB=180°﹣40°=140°,
∵∠BDC=90°,
∴∠DBC+∠DCB=90°,
∴∠ABD+∠ACD=140°﹣90°=50°,
∵BE、CE分别平分∠ABD和∠ACD,BF、CF分别平分∠ABE和∠ACE,
∴∠FBD+∠FCD=×50°=37.5°,
∴∠FBC+∠FCB=37.5°+90°=127.5°,
∴∠F=180°﹣127.5°=52.5°,
18.105° 150°
【详解】
解:设∠BAP=α,则∠APC=α+30°,
∵∠BAC=90°,
∴∠PCA=60°,∠PAC=90°-α,
∵AI、CI分别平分∠PAC,∠PCA,
∴∠IAC=∠PAC,∠ICA=∠PCA,
∴∠AIC=180°-(∠IAC+∠ICA)
=180°-(∠PAC+∠PCA)
=180°-(90°-α+60°)
=α+105°,
∵0<α<90°,
∴105°<α+105°<150°,即105°<∠AIC<150°,
∴m=105°,n=150°.
19.36°.
【详解】
∵BA⊥AC,
∴∠BAC=90°,
∵∠ABC=54°,
∴∠C=90°-54°=36°,
∵AE//BC,
∴∠EAC=∠C=36°.
20.(1);(2)
【详解】
解:(1)∵AE是BC边上的高,
∴∠E=90°,
又∵∠ACB=100°,∠ACB+∠ACE=180°,
∴∠ACE=80°,
∵∠CAE+∠ACE+∠E=180°
∴∠CAE=180°-90°-80°=10°;
(2)∵AD是BC上的中线,DC=3,
∴D为BC的中点,
∴BC=2DC=6,
∵AE是BC边上的高,S△ABC=12,
∴S△ABC=BC?AE,
即×6×AE=12,
∴AE=4.
21.(1)35°;(2)125°或25°或55°
【详解】
解:(1)∵,,
∴,
∵BP平分,
∴,
∵,
∴.
(2)①当时,延长至,
,,
∴,
②当时,,
∴,
③当时,,,
∴.
22.(1)150°(2)证明见解析;(3).
【详解】
解:(1)作EF//AB,
∴∠ABE=∠BEF,
又∵,
∴EF//CD,
∴∠DEF=∠EDC,
∴,
∵,
∴,
故答案为:150°.
(2)∵分别平分,
∴,
由(1)得,
作PG//AB,与(1)同理可证,
∴
(3)如下图,延长BM、DN,交于E,
∵,
∴∠EMN=47°,∠ENM=35°,
∴∠E=180°-∠EMN-∠ENM=98°,
∴由(2)可知.
23.(1)15°,105°;(2)①不变,60°;②∠1=40°,∠2=20°,∠α=85°;③69°≤α<90°
【详解】
解:(1),
当时,,
而,
,解得;
当时,,
此时,
,解得;
故答案为,;
(2)①与度数的和不变.
连接,如图3,
在中,,
,
在中,,
即,
;
②根据题意得,解得;
,
即,
;
③,,
,
,
,
即,
,
,解得,
的度数范围为.
_21?????????è?????(www.21cnjy.com)_
人教版2021年八年级上册数学同步练习卷
11.2与三角形有关的角
11.2.1 三角形的内角
一、单选题
1.如果三角形的两个内角都小于,那么这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
2.如图,直线,三角尺的直角顶点在直线m上,且三角尺的直角被直线m平分,若,则下列结论错误的是( )
A. B. C. D.
3.如图,已知直线AB∥CD,直线AC和BD相交于点E,若∠ABE=75°,∠ACD=35°,则∠AEB等于( )
A.60° B.70° C.75° D.80°
4.如图,直线,点、在上,射线交于点,平分交于点,若,则的度数是( )
A. B. C. D.
5.将一副直角三角板按如图放置(其中),使含角的三角板的较长直角边与等腰直角三角板的斜边平行,则图中的度数为( )
A. B. C. D.
6.如图,,,重足为,,则等于( )
A.40° B.45° C.50° D.60°
7.如图,将一副三角尺按图中所示位置摆放,点在上,其中,,,,,则的度数是( )
A. B. C. D.
8.两个直角三角板如图摆放,其中,,,AB与DF交于点M.若,则的大小为( )
A. B. C. D.
9.如图,平分交于点E,,,M,N分别是延长线上的点,和的平分线交于点F.下列结论:①;②;③平分;④为定值.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
10.如图,在中,是的平分线,是外角的平分线,与相交于点,若,则是( )
A. B. C. D.
11.若△ABC内有一个点P1,当P1、A、B、C没有任何三点在同一直线上时,如图1,可构成3个互不重叠的小三角形;若△ABC内有两个点P1、P2,其它条件不变,如图2,可构成5个互不重叠的小三角形:……若△ABC内有n个点,其它条件不变,则构成若干个互不重叠的小三角形,这些小三角形的内角和为()
A.n·180° B.(n+2)·180° C.(2n-1)·180° D.(2n+1)·180°
12.如图所示,在四边形纸片ABCD中,∠A=80°,∠B=70°,将纸片沿着MN折叠,使C,D分别落在直线AB上的,处,则∠+∠等于( )
A.50° B.60° C.70° D.80°
二、填空题
13.在中,,,则的度数是______.
14.一个三角形三个内角的比是,它的面积是12,则它的周长是______.
15.如图,平面直角坐标系中的两个点,过C作轴于B,过B作交y轴于D,且,分别平分,,则的度数为______________________.
16.如图,把沿线段折叠,使点A落在点F处,,若,则__.
17.如图,△ABC中,∠BDC=90°,BE、CE分别平分∠ABD和∠ACD,BF、CF分别平分∠ABE和∠ACE,若∠A=40°,则∠F=__°.
18.如图,在中,,,点P是的动点(不与点B,C重合),、分别是和的角平分线,的取值范围为,则_______,________.
三、解答题
19.如图,直线AE//BC,BA⊥AC,若∠ABC=54°,求∠EAC的度数.
20.如图,中,是边上的中线,是边上的高.
(1)若,求的度数;
(2)若,,求高的长.
21.如图,中,平分,点D为射线上一动点.
(1)连接,若,求的度数;
(2)连接,若所在的直线垂直于的一边,则所有满足条件的的度数为__________.
22.已知,
(1)若,则________,
(2)如图1,分别平分,试说明.;
(3)如图2.若分别平分.求的度数.
23.如图1,含角的直角三角板与含角的直角三角板的斜边在同一直线上,D为的中点,将直角三角板绕点D按逆时针方向旋转,在旋转过程中:
(1)如图2,当________时,;当______时,;
(2)如图③,当直角三角板的边、分别交、的延长线于点M、N时;
①与度数的和是否变化?若不变,求出与度数的和;若变化,请说明理由;
②若使得,求出、的度数,并直接写出此时的度数;
③若使得,求的度数范围.
参考答案
1.C
【详解】
设中
是钝角三角形
故选C.
2.D
【详解】
首先根据三角尺的直角被直线m平分,
∴∠6=∠7=45°;
A、∵∠1=60°,∠6=45°,∴∠8=180°-∠1-∠6=180-60°-45°=75°,m∥n,∴∠2=∠8=75°结论正确,选项不合题意;
B、∵∠7=45°,m∥n,∴∠3=∠7=45°,结论正确,选项不合题意;
C、∵∠8=75°,∴∠4=180-∠8=180-75°=105°,结论正确,选项不合题意;
D、∵∠7=45°,∴∠5=180-∠7=180-45°=135°,结论错误,选项符合题意.
3.B
【详解】
解:∵AB∥CD,
∴∠BAE=∠ACD=35°.
∵∠AEB+∠BAE+∠ABE=180°,∠ABE=75°,
∴∠AEB=70°.
4.B
【详解】
解:如图,
∵,
∴∠3=∠1=80°
∴∠ABD=180°-80°=100°
∵平分
∴
又
∴
5.B
【详解】
解:如图:根据特殊直角三角形的性质可知,∠A=45°,∠F=30°,
∵AB∥EF,
∴∠ACF=∠A=45°,
∴∠CHF=180°-∠F-∠ACF=180°-30°-45°=105°,
∴∠1=180°-∠CHF=108°-105°=75°,
故选:B.
6.C
【详解】
解:∵,
∴∠ACB=90°,
∵,
∴∠ABC=90°-=50°,
∵
∴,
7.A
【详解】
解:设AB与EF交于点M,
∵,
∴,
∵,,
∴,
∴,
∵,
∴=,
8.C
【详解】
由图可得
∵,
∴
∴
9.C
【详解】
解:∵AB⊥BC,AE⊥DE,
∴∠1+∠AEB=90°,∠DEC+∠AEB=90°,
∴∠1=∠DEC,
又∵∠1+∠2=90°,
∴∠DEC+∠2=90°,
∴∠C=90°,
∴∠B+∠C=180°,
∴AB∥CD,故①正确;
∴∠ADN=∠BAD,
∵∠ADC+∠ADN=180°,
∴∠BAD+∠ADC=180°,
又∵∠AEB≠∠BAD,
∴AEB+∠ADC≠180°,故②错误;
∵∠4+∠3=90°,∠2+∠1=90°,而∠3=∠1,
∴∠2=∠4,
∴ED平分∠ADC,故③正确;
∵∠1+∠2=90°,
∴∠EAM+∠EDN=360°-90°=270°.
∵∠EAM和∠EDN的平分线交于点F,
∴∠EAF+∠EDF=×270°=135°.
∵AE⊥DE,
∴∠3+∠4=90°,
∴∠FAD+∠FDA=135°-90°=45°,
∴∠F=180°-(∠FAD+∠FDA)=180-45°=135°,故④正确.
10.C
【详解】
解:∵是的平分线,
∴∠ABC=2∠DBC,
同理,∠ACM=2∠DCM,
∵∠ACM=∠A+∠ABC,
∴2∠DCM=∠A+2∠DBC
∵∠DCM=∠D+∠DBC,
∴∠A=2∠D,
∵,
∴,
11.D
【详解】
图1中,当△ABC内只有1个点时,可分割成3个互不重叠的小三角形;
图2中,当△ABC内只有2个点时,可分割成5个互不重叠的小三角形;
图3中,当△ABC内只有3个点时,可分割成7个互不重叠的小三角形;
根据以上规律,当△ABC内有n个点(P1,P2,…,Pn)时,可以把△ABC分割成S=2n+1个互不重叠的三角形,所以这些小三角形的内角和为(2n+1)·180°.
12.B
【详解】
∵∠A=80°,∠B=70°,
∴∠D+∠C=360°?∠A?∠B=210°,
由折叠性质可得:∠=∠D,∠=∠C,
∴∠+∠=210°,
∴∠+∠=360°?(∠+∠)=150°,
∴∠+∠=360°?(∠+∠)?(∠A+∠B)=60°,
13.75°
【详解】
.
14.
【详解】
解:此三角形各角的度数分别是:
,
,
由此知三角形是等腰直角三角形;
设直角边为a,根据勾股定理可知斜边为,
∵,
即,
∴,
则斜边应是,
那么,
即,
故答案为:.
15.45°
【详解】
连接AD,如图所示:
∵BD∥AC,
∴∠BAC=∠ABD,
∵∠ABD+∠ODB=90°,
∴∠BAC+∠ODB=90°,
∵AE,DE分别平分∠CAB,∠ODB,
∴,
∴,
∵∠AED+∠EAD+∠EDA=180°,即∠AED+∠EAO+∠OAD+∠EDO+∠ODA=180°,
∵∠OAD+∠ODA=90°,
∴∠AED+45°+90°=180°,
∴∠AED=45°.
16.60
【详解】
解:∵BC∥DE,若∠B=60°,
∴∠ADE=60°,
又∵△ABC沿线段DE折叠,使点A落在点F处,
∴∠ADE=∠EDF=60°,
∴∠BDF=180°-60°-60°=60°,
17.52.5.
【详解】
解:∵∠A=40°,
∴∠ABC+∠ACB=180°﹣40°=140°,
∵∠BDC=90°,
∴∠DBC+∠DCB=90°,
∴∠ABD+∠ACD=140°﹣90°=50°,
∵BE、CE分别平分∠ABD和∠ACD,BF、CF分别平分∠ABE和∠ACE,
∴∠FBD+∠FCD=×50°=37.5°,
∴∠FBC+∠FCB=37.5°+90°=127.5°,
∴∠F=180°﹣127.5°=52.5°,
18.105° 150°
【详解】
解:设∠BAP=α,则∠APC=α+30°,
∵∠BAC=90°,
∴∠PCA=60°,∠PAC=90°-α,
∵AI、CI分别平分∠PAC,∠PCA,
∴∠IAC=∠PAC,∠ICA=∠PCA,
∴∠AIC=180°-(∠IAC+∠ICA)
=180°-(∠PAC+∠PCA)
=180°-(90°-α+60°)
=α+105°,
∵0<α<90°,
∴105°<α+105°<150°,即105°<∠AIC<150°,
∴m=105°,n=150°.
19.36°.
【详解】
∵BA⊥AC,
∴∠BAC=90°,
∵∠ABC=54°,
∴∠C=90°-54°=36°,
∵AE//BC,
∴∠EAC=∠C=36°.
20.(1);(2)
【详解】
解:(1)∵AE是BC边上的高,
∴∠E=90°,
又∵∠ACB=100°,∠ACB+∠ACE=180°,
∴∠ACE=80°,
∵∠CAE+∠ACE+∠E=180°
∴∠CAE=180°-90°-80°=10°;
(2)∵AD是BC上的中线,DC=3,
∴D为BC的中点,
∴BC=2DC=6,
∵AE是BC边上的高,S△ABC=12,
∴S△ABC=BC?AE,
即×6×AE=12,
∴AE=4.
21.(1)35°;(2)125°或25°或55°
【详解】
解:(1)∵,,
∴,
∵BP平分,
∴,
∵,
∴.
(2)①当时,延长至,
,,
∴,
②当时,,
∴,
③当时,,,
∴.
22.(1)150°(2)证明见解析;(3).
【详解】
解:(1)作EF//AB,
∴∠ABE=∠BEF,
又∵,
∴EF//CD,
∴∠DEF=∠EDC,
∴,
∵,
∴,
故答案为:150°.
(2)∵分别平分,
∴,
由(1)得,
作PG//AB,与(1)同理可证,
∴
(3)如下图,延长BM、DN,交于E,
∵,
∴∠EMN=47°,∠ENM=35°,
∴∠E=180°-∠EMN-∠ENM=98°,
∴由(2)可知.
23.(1)15°,105°;(2)①不变,60°;②∠1=40°,∠2=20°,∠α=85°;③69°≤α<90°
【详解】
解:(1),
当时,,
而,
,解得;
当时,,
此时,
,解得;
故答案为,;
(2)①与度数的和不变.
连接,如图3,
在中,,
,
在中,,
即,
;
②根据题意得,解得;
,
即,
;
③,,
,
,
,
即,
,
,解得,
的度数范围为.
_21?????????è?????(www.21cnjy.com)_
