山东省梁山一中2011-2012学年高二下学期期中试题数学理
文档属性
| 名称 | 山东省梁山一中2011-2012学年高二下学期期中试题数学理 |  | |
| 格式 | zip | ||
| 文件大小 | 233.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-28 10:22:10 | ||
图片预览



文档简介
梁山一中11-12学年高二下学期期中考试
数学(理)试题
选择题 (本大题共12个小题;每小题5分,共60分.在每小题给出的4个选项中,只有一项符合题目要求.)
1.已知复数是虚数单位,则复数的虚部是( )
A. B. C. D.
2.若,且,则实数的值是( )
A . -1 B . 0 C . 1 D . -2
3.曲线在点(1,-3)处的切线倾斜角为( )
A. B . C. D.
4. 已知函数,则( )
A. B. C. D.
5.函数的图象上一点处的切线的斜率为( )
A. B. C. D.
6.用数学归纳法证明()时,从“到”左边需增乘的代数式为( )
A. B. C. D.
7.函数的图象如图所示,若,则等于( )
A. B.
C.0 D.
8.续抛两枚骰子分别得到的点数是,,则向量与向量垂直的概率是( )
A. B. C. D.
9.利用数学归纳法证明“”,在验证成立时,左边应该是. ( )
A. B. C. D.
10. 已知二次函数的导数为,,对于任意实数都有,则的最小值为( )
A. B. C. D.
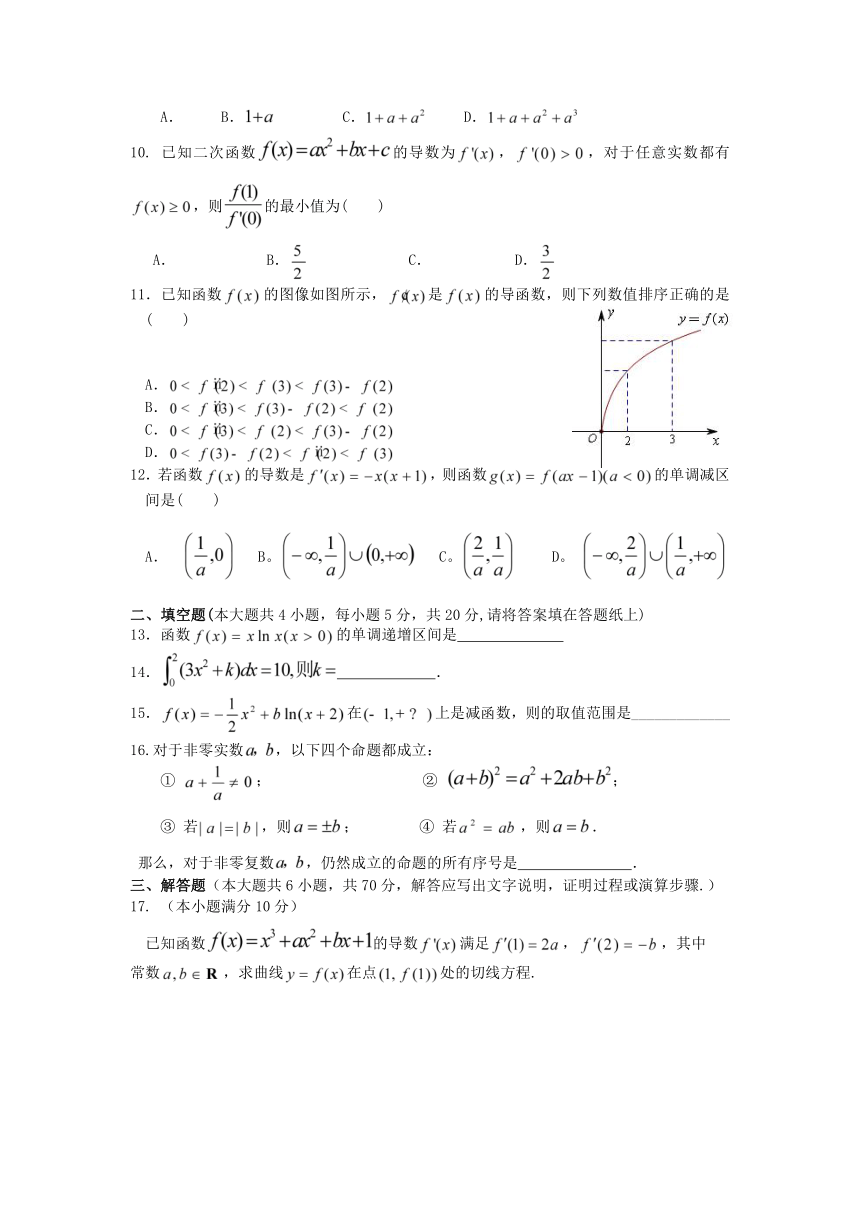
11.已知函数的图像如图所示,是的导函数,则下列数值排序正确的是( )
A.
B.
C.
D.
12.若函数的导数是,则函数的单调减区间是( )
A. B。 C。 D。
二、填空题(本大题共4小题,每小题5分,共20分,请将答案填在答题纸上)
13.函数的单调递增区间是
14. .
15.在上是减函数,则的取值范围是_____________
16.对于非零实数,以下四个命题都成立:
① ; ② ;
③ 若,则; ④ 若,则.
那么,对于非零复数,仍然成立的命题的所有序号是 .
三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.)
17. (本小题满分10分)
已知函数的导数满足,,其中
常数,求曲线在点处的切线方程.
18. (本小题满分12分)
如图,在直三棱柱中, AB=1,,∠ABC=60.
(1 )证明:;
(2)求二面角A——B的正切值。
19. (本小题满分12分)
设的垂直平分线。
(1)当且仅当
(2)当直线的斜率为2时,求轴上截距的取值范围。
20. (本小题满分12分)
如图,四棱锥中,底面为平行四边形,,,⊥底面.
(1)证明:平面平面;
(2)若二面角为,求与平面所成角的正弦值。
21. (本小题满分12分)
统计表明,某种型号的汽车在匀速行驶中每小时耗油量y(升)关于行驶速度x(千米/小时)的函数解析式可以表示为:(≤120).已知甲、乙两地相距100千米。
(Ⅰ)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(Ⅱ)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
22. (本小题满分12分)
已知函数.
(1)若曲线在处的切线的方程为,求实数的值;
(2)求证:≥0恒成立的充要条件是;
(3)若,且对任意,都有,求实数的取值范围。
参考答案:
1-5 DDADD 6-10 BCBCC 11-12 BA
13.; 14.1 ; 15. ; 16.②④
17. 解:因为,所以
令得.
由已知,所以. 解得.
又令得.
由已知 所以解得
所以,.
又因为
故曲线处的切线方程为
,即.
18.(1)证: 三棱柱为直三棱柱,
在中,,由正弦定理
,又
(2)解如图,作交于点D点,连结BD,
由三垂线定理知
为二面角的平面角
在
19.解:(1)
依题意不同时为0
上述条件等价于
即当且仅当
(2);
过点
。
,则
,由
于是
20. (1)证明:平面平面;
(2)若二面角为,求与平面所成角的正弦值。
(1)证明:∵ ∴
又∵⊥底面 ∴
又∵ ∴平面
而平面
∴平面平面
(2)由(1)所证,平面
所以∠即为二面角P-BC-D的平面角,即∠
而,所以
分别以、、为轴、轴、轴建立空间直角坐标系。
则,,,
所以,,,
设平面的法向量为,则
即 可解得
∴与平面所成角的正弦值为
21. 解: (1)当x=40时,汽车从甲地到乙地行驶了小时,
要耗油(.
答:当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地耗油17.5升.
(2)当速度为x千米/小时,汽车从甲地到乙地行驶了设耗油量为h(x)升,依题意得h(x)=()·,
(x)= 其中0<x≤120
令(x)=0,得x=80.
当x∈(0,80)时,(x)<0,h(x)是减函数;
当x∈(80,120)时,(x)>0,h(x)是增函数.
∴当x=80时,h(x)取到极小值h(80)=11.25.
因为h(x)在(0,120)上只有一个极值,所以它是最小值.
22.
。
(2)①充分性
所以当
上是增函数,当,所以函数在(0,1)上是减函数,所以
②必要性
(i)当时,恒成立,所以函数在(0,+)上是增函数。而,所以当
综上所述,恒成立的充要条件是a=1.
(3)由(2)可知
当a<0时,函数f(x)在上是增函数,又函数在是减函数。
,则
(第7题图)
C
B
A
C1
B1
A1
数学(理)试题
选择题 (本大题共12个小题;每小题5分,共60分.在每小题给出的4个选项中,只有一项符合题目要求.)
1.已知复数是虚数单位,则复数的虚部是( )
A. B. C. D.
2.若,且,则实数的值是( )
A . -1 B . 0 C . 1 D . -2
3.曲线在点(1,-3)处的切线倾斜角为( )
A. B . C. D.
4. 已知函数,则( )
A. B. C. D.
5.函数的图象上一点处的切线的斜率为( )
A. B. C. D.
6.用数学归纳法证明()时,从“到”左边需增乘的代数式为( )
A. B. C. D.
7.函数的图象如图所示,若,则等于( )
A. B.
C.0 D.
8.续抛两枚骰子分别得到的点数是,,则向量与向量垂直的概率是( )
A. B. C. D.
9.利用数学归纳法证明“”,在验证成立时,左边应该是. ( )
A. B. C. D.
10. 已知二次函数的导数为,,对于任意实数都有,则的最小值为( )
A. B. C. D.
11.已知函数的图像如图所示,是的导函数,则下列数值排序正确的是( )
A.
B.
C.
D.
12.若函数的导数是,则函数的单调减区间是( )
A. B。 C。 D。
二、填空题(本大题共4小题,每小题5分,共20分,请将答案填在答题纸上)
13.函数的单调递增区间是
14. .
15.在上是减函数,则的取值范围是_____________
16.对于非零实数,以下四个命题都成立:
① ; ② ;
③ 若,则; ④ 若,则.
那么,对于非零复数,仍然成立的命题的所有序号是 .
三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.)
17. (本小题满分10分)
已知函数的导数满足,,其中
常数,求曲线在点处的切线方程.
18. (本小题满分12分)
如图,在直三棱柱中, AB=1,,∠ABC=60.
(1 )证明:;
(2)求二面角A——B的正切值。
19. (本小题满分12分)
设的垂直平分线。
(1)当且仅当
(2)当直线的斜率为2时,求轴上截距的取值范围。
20. (本小题满分12分)
如图,四棱锥中,底面为平行四边形,,,⊥底面.
(1)证明:平面平面;
(2)若二面角为,求与平面所成角的正弦值。
21. (本小题满分12分)
统计表明,某种型号的汽车在匀速行驶中每小时耗油量y(升)关于行驶速度x(千米/小时)的函数解析式可以表示为:(≤120).已知甲、乙两地相距100千米。
(Ⅰ)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(Ⅱ)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
22. (本小题满分12分)
已知函数.
(1)若曲线在处的切线的方程为,求实数的值;
(2)求证:≥0恒成立的充要条件是;
(3)若,且对任意,都有,求实数的取值范围。
参考答案:
1-5 DDADD 6-10 BCBCC 11-12 BA
13.; 14.1 ; 15. ; 16.②④
17. 解:因为,所以
令得.
由已知,所以. 解得.
又令得.
由已知 所以解得
所以,.
又因为
故曲线处的切线方程为
,即.
18.(1)证: 三棱柱为直三棱柱,
在中,,由正弦定理
,又
(2)解如图,作交于点D点,连结BD,
由三垂线定理知
为二面角的平面角
在
19.解:(1)
依题意不同时为0
上述条件等价于
即当且仅当
(2);
过点
。
,则
,由
于是
20. (1)证明:平面平面;
(2)若二面角为,求与平面所成角的正弦值。
(1)证明:∵ ∴
又∵⊥底面 ∴
又∵ ∴平面
而平面
∴平面平面
(2)由(1)所证,平面
所以∠即为二面角P-BC-D的平面角,即∠
而,所以
分别以、、为轴、轴、轴建立空间直角坐标系。
则,,,
所以,,,
设平面的法向量为,则
即 可解得
∴与平面所成角的正弦值为
21. 解: (1)当x=40时,汽车从甲地到乙地行驶了小时,
要耗油(.
答:当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地耗油17.5升.
(2)当速度为x千米/小时,汽车从甲地到乙地行驶了设耗油量为h(x)升,依题意得h(x)=()·,
(x)= 其中0<x≤120
令(x)=0,得x=80.
当x∈(0,80)时,(x)<0,h(x)是减函数;
当x∈(80,120)时,(x)>0,h(x)是增函数.
∴当x=80时,h(x)取到极小值h(80)=11.25.
因为h(x)在(0,120)上只有一个极值,所以它是最小值.
22.
。
(2)①充分性
所以当
上是增函数,当,所以函数在(0,1)上是减函数,所以
②必要性
(i)当时,恒成立,所以函数在(0,+)上是增函数。而,所以当
综上所述,恒成立的充要条件是a=1.
(3)由(2)可知
当a<0时,函数f(x)在上是增函数,又函数在是减函数。
,则
(第7题图)
C
B
A
C1
B1
A1
同课章节目录
