分式方程公开课
图片预览







文档简介
(共24张PPT)
分式方程
温故知新
解方程:
解:去分母 3(x-1)+2(2x+1)=6
去括号 3x-3+4x+2=6
移项 3x+4x=3+3-2
合并同类项 7x=7
系数化为1 x=7
你做对了吗
学习目标:
1、掌握分式方程的概念;
2、理解分式方程的解题思路;
3、初步掌握解简单的分式方程的一般步骤;
4、了解分式方程产生增根的原因及掌握验根的方法。
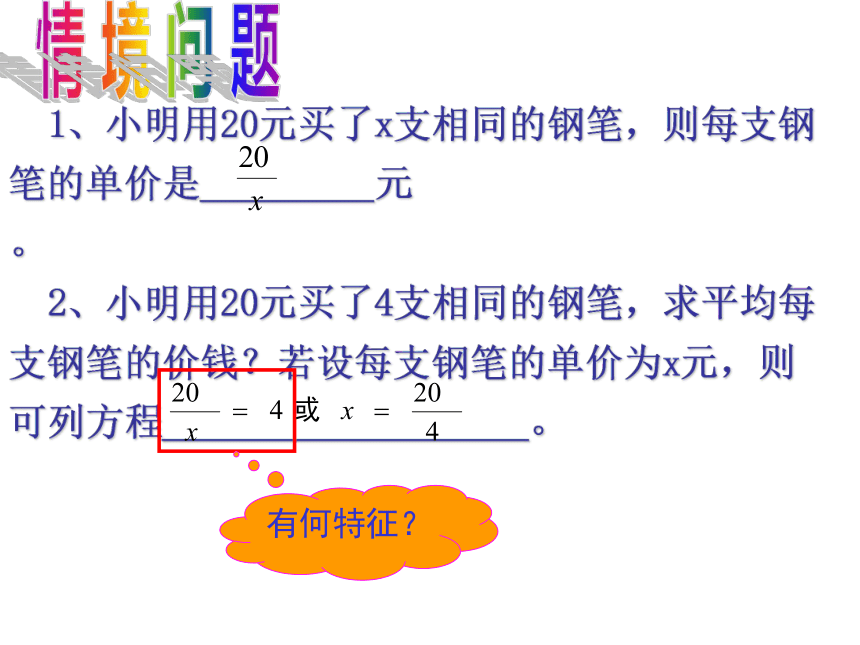
1、小明用20元买了x支相同的钢笔,则每支钢笔的单价是 元
。
2、小明用20元买了4支相同的钢笔,求平均每支钢笔的价钱?若设每支钢笔的单价为x元,则可列方程 。
有何特征?
概括:
分母中含有未知数的方程,叫做分式方程
方程 与 有什么不同?
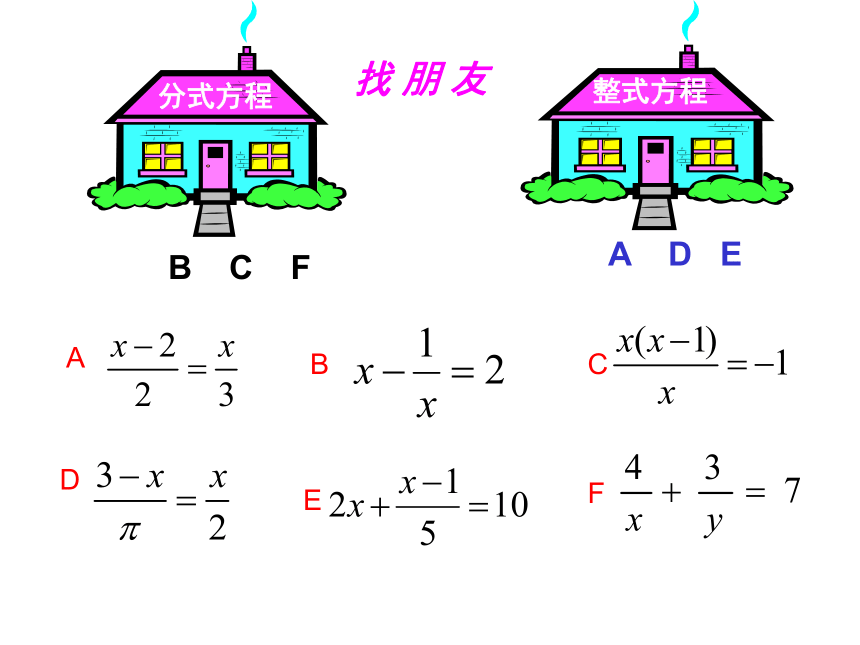
议一议
找 朋 友
整式方程
分式方程
A
B
C
D
E
F
B C F
A D E
解得:
下面我们一起研究如何解这个分式方程:
解:方程两边同乘以 x,得:
检验:将x=5代入分式方程,左边=4=右边,所以x=5是原分式方程的解。
讨论:怎样化为整式方程?
解:方程两边同乘以最简公分母 得 ,
检验:将
代入原分式方程检验发现分母
相应的分式无意义,因此x=3不是分式方程的解,此分式方程无解
试解方程
解得:
解:方程两边同乘以最简公分母 得 ,
检验:将
代入原分式方程检验发现分母
观察方程①方程②中x取值范围相同吗?
试解方程
解得:
②
①
增根的定义
产生的原因:分式方程两边同乘以一个零因式后,所得的根是整式方程的根,而不是分式方程的根.
····
····
增根:在去分母,将分式方程转化为整式方程的过程中出现的不适合于原方程的根.
使分母值为零的根
······
因此解分式方程可能产生增根,解分式方程必须检验 ( 代入最简公分母检验)
作 业
1.去分母(在方程的两边都乘以最简公分母,约去分母,化成整式方程).
2.解这个整式方程.
3.检验(把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解,是增根,必须舍去).
一化二解三检验
解分式方程的一般步骤
例1 解方程
x(x-3)
2x=3(x-3)
x=9
x=9
x(x-3)
x(x-3)= 54 ≠0
x=9
解:方程两边同乘以最简公分母 得,
解得:
检验: 把 代入最简公分母
∴原方程的解是
解方程
解:方程两边同乘以最简公分母(x-2)得,
x-1=3(x-2)
解得: x=
检验:把x= 代入最简公分母(x-2)
是原分式方程的解
还有其它解法吗
解方程
解:方程两边同乘以最简公分母(2-x)得,
-x+1=3(2-x)
解得: x=
检验:把x= 代入最简公分母(2-x)
是原分式方程的解
解法二
智力大比拼
收获
练习2
练习1
小测
体会
小结
解 方 程:
巩固练习
1. 分式方程 的最简公分母是 .
X=1
2.如果方程 有增根,那么增根为 .
X-2或2-X
练习2
解关于x的方程 产生增根,
则常数m的值等于( )
(A)-2 (B)-1 (C ) 1 (D) 2
A
解分式方程容易犯的错误有:
(1)去分母时,原方程的整式部分漏乘.
(2)约去分母后,分子是多项式时, 要注意添括号.(因分数线有括号的作用)
(3)增根不舍掉。
1、判断下列各式哪些是分式方程,哪些是整式方程。
是分式方程有 ,是整式方程有 。
3、解方程
小测:
2.若方程 无解,则m= .
X=1
X=5
(4)(5)
(1)(2)(6)
-3
1. 认识了分式方程
2. 解分式方程的一般步骤
1、解分式方程的思路是:
分式方程
整式方程
去分母
2、解分式方程的一般步骤:
一化二解三检验
1、去分母(在方程的两边都乘以最简公分母,约去分母,化成整式方程).
2、解这个整式方程.
3、检验(把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解,是增根,必须舍去)..
1. 书: 习题16.3
第一题
2. 学习指导
3. 预习新课
分式方程
温故知新
解方程:
解:去分母 3(x-1)+2(2x+1)=6
去括号 3x-3+4x+2=6
移项 3x+4x=3+3-2
合并同类项 7x=7
系数化为1 x=7
你做对了吗
学习目标:
1、掌握分式方程的概念;
2、理解分式方程的解题思路;
3、初步掌握解简单的分式方程的一般步骤;
4、了解分式方程产生增根的原因及掌握验根的方法。
1、小明用20元买了x支相同的钢笔,则每支钢笔的单价是 元
。
2、小明用20元买了4支相同的钢笔,求平均每支钢笔的价钱?若设每支钢笔的单价为x元,则可列方程 。
有何特征?
概括:
分母中含有未知数的方程,叫做分式方程
方程 与 有什么不同?
议一议
找 朋 友
整式方程
分式方程
A
B
C
D
E
F
B C F
A D E
解得:
下面我们一起研究如何解这个分式方程:
解:方程两边同乘以 x,得:
检验:将x=5代入分式方程,左边=4=右边,所以x=5是原分式方程的解。
讨论:怎样化为整式方程?
解:方程两边同乘以最简公分母 得 ,
检验:将
代入原分式方程检验发现分母
相应的分式无意义,因此x=3不是分式方程的解,此分式方程无解
试解方程
解得:
解:方程两边同乘以最简公分母 得 ,
检验:将
代入原分式方程检验发现分母
观察方程①方程②中x取值范围相同吗?
试解方程
解得:
②
①
增根的定义
产生的原因:分式方程两边同乘以一个零因式后,所得的根是整式方程的根,而不是分式方程的根.
····
····
增根:在去分母,将分式方程转化为整式方程的过程中出现的不适合于原方程的根.
使分母值为零的根
······
因此解分式方程可能产生增根,解分式方程必须检验 ( 代入最简公分母检验)
作 业
1.去分母(在方程的两边都乘以最简公分母,约去分母,化成整式方程).
2.解这个整式方程.
3.检验(把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解,是增根,必须舍去).
一化二解三检验
解分式方程的一般步骤
例1 解方程
x(x-3)
2x=3(x-3)
x=9
x=9
x(x-3)
x(x-3)= 54 ≠0
x=9
解:方程两边同乘以最简公分母 得,
解得:
检验: 把 代入最简公分母
∴原方程的解是
解方程
解:方程两边同乘以最简公分母(x-2)得,
x-1=3(x-2)
解得: x=
检验:把x= 代入最简公分母(x-2)
是原分式方程的解
还有其它解法吗
解方程
解:方程两边同乘以最简公分母(2-x)得,
-x+1=3(2-x)
解得: x=
检验:把x= 代入最简公分母(2-x)
是原分式方程的解
解法二
智力大比拼
收获
练习2
练习1
小测
体会
小结
解 方 程:
巩固练习
1. 分式方程 的最简公分母是 .
X=1
2.如果方程 有增根,那么增根为 .
X-2或2-X
练习2
解关于x的方程 产生增根,
则常数m的值等于( )
(A)-2 (B)-1 (C ) 1 (D) 2
A
解分式方程容易犯的错误有:
(1)去分母时,原方程的整式部分漏乘.
(2)约去分母后,分子是多项式时, 要注意添括号.(因分数线有括号的作用)
(3)增根不舍掉。
1、判断下列各式哪些是分式方程,哪些是整式方程。
是分式方程有 ,是整式方程有 。
3、解方程
小测:
2.若方程 无解,则m= .
X=1
X=5
(4)(5)
(1)(2)(6)
-3
1. 认识了分式方程
2. 解分式方程的一般步骤
1、解分式方程的思路是:
分式方程
整式方程
去分母
2、解分式方程的一般步骤:
一化二解三检验
1、去分母(在方程的两边都乘以最简公分母,约去分母,化成整式方程).
2、解这个整式方程.
3、检验(把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解,是增根,必须舍去)..
1. 书: 习题16.3
第一题
2. 学习指导
3. 预习新课
