6.3.2 一次函数的图像-苏科版数学八年级上册课件(19张)
文档属性
| 名称 | 6.3.2 一次函数的图像-苏科版数学八年级上册课件(19张) |  | |
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-09 08:35:40 | ||
图片预览





文档简介
(共19张PPT)
6.3
一次函数的图像(2)
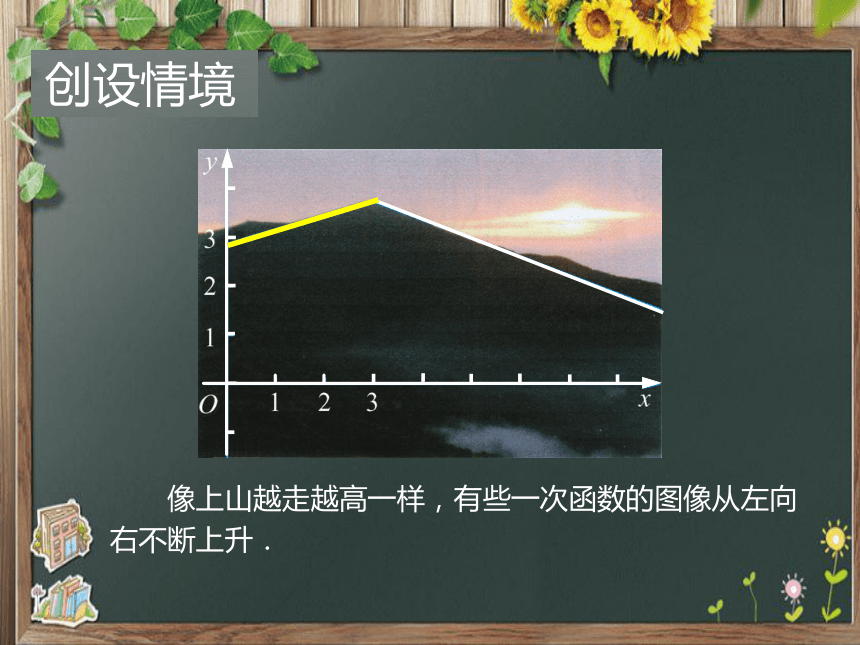
像上山越走越高一样,有些一次函数的图像从左向右不断上升.
创设情境
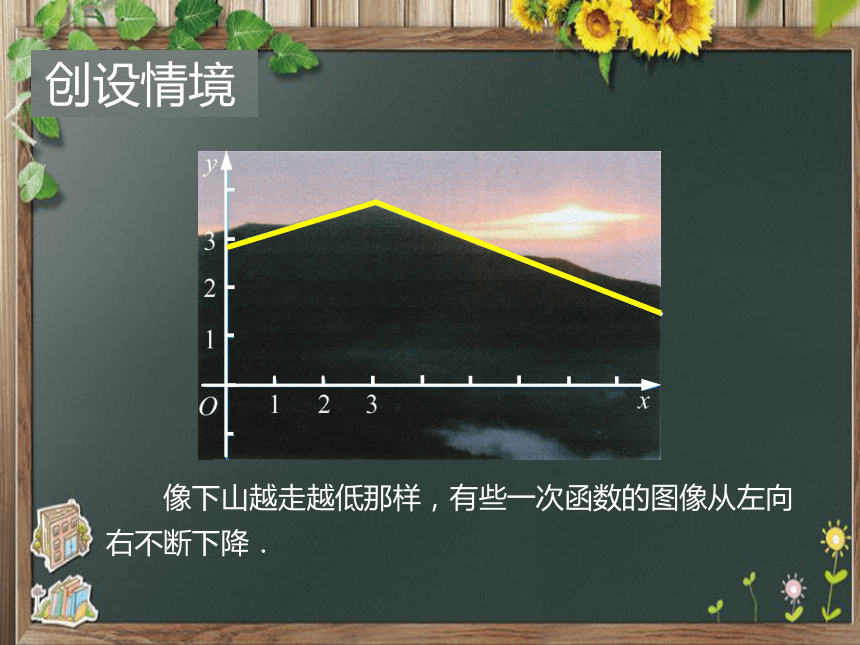
像下山越走越低那样,有些一次函数的图像从左向右不断下降.
创设情境
观察这两个函数的图像,你有什么发现?
x的值越大,对应的y值也越大。
x的值越大,对应的y值越小。
1、你觉得是什么决定了这个函数图像会上升还是下降?
2、请你写一个一次函数并画出图像来支持或反驳上面的猜想。
探索活动1
(1)如果k>0,那么函数值y随自变量x增大而增大,图像经
过一、三象限;
在一次函数y=kx+b
中:
(2)如果k<0,那么函数值y随自变量x增大而减小,图像经
过二、四象限。
小结1
(1)y=-1.6
x+4,(2)y=0.5
x-5,
(3)y=4
x,(4)y=-
x-3,
(5)y=5
x-7.
已知函数:
y
值随
x
值增大而增大的函数是
;
(2)(3)(5)
从左往右,图像是下降的函数是
.
(1)(4)
3
2
请你写一个和y=4
x
的图像平行的一次函数
.
考考你
通过刚才的活动,我们发现一次函数y=kx+b中,k的符号、绝对值等等对函数图像有决定性的影响。
那么,一次函数表达式中b的值又对函数图像有什么影响呢?
研究一次函数
y1=2x
、y2=2x+3、
y3=2x-3
的关系。
0
x
y
y=2x
3
-3
y=2x+3
y=2x-3
探索活动2
你觉得这里的b对函数图像产生了什么影响?
x
y
0
y=kx(b=0)
一般地,正比例函数y=kx的图像是经过原点的一条直线.
如果b>0,那么一次函数y=kx+b的图像可以由正比例函数y=kx向上平移b个单位长度得到。
b>0,交y轴于正半轴
b<0,交y轴于负半轴
y=kx+b(b>0)
y=kx+b(b<0)
如果b<0,那么一次函数y=kx+b的图像可以由正比例函数y=kx向下平移|b|个单位长度得到。
(1)将一次函数y=2x-3的图像沿y轴向上平移8个单位长度,所得直线的函数表达式为(
)
A、y=2x-5
B、y=2x+5
C、y=2x+8
D、y=2x-8
(2)将直线y=x+b沿y轴向下平移3个单位长度,点A(1,2)落在平移后的直线上,则b的值为______.
4
B
考考你
一次函数
y=k
x+b
(
k、b为常数,且
k≠0)中k、
b
的值对函数图像的影响.
图像特征
大致图像
k>0
b>0
上升,
交y轴于正半轴.
b=0
上升,
交点在原点.
b<0
上升,
交y轴于负半轴.
x
y
0
x
y
0
x
y
0
归纳小结
一次函数
y=k
x+b
(
k、b为常数,且
k≠0)中k、
b
的值对函数图像的影响.
图像特征
大致图像
k<0
b>0
下降,
交y轴于正半轴.
b=0
下降,
交点在原点.
b<0
下降,
交y轴于负半轴.
x
y
0
x
y
0
x
y
0
归纳总结
归纳小结
例1.一次函数y=2x-3的图像经过(
)
A.第一、二、三象限.
B.第一、二、四象限.
C.第一、三、四象限.
D.第二、三、四象限.
C
例题与变式
变式1.一次函数y=ax+b
的图像经过第一、二、四象限,则一次函数y=bx+a的图像经过(
)
C
A.第一、二、三象限.
B.第一、二、四象限.
C.第一、三、四象限.
D.第二、三、四象限.
变式2.A(x1,y1)、B(x2,y2)是直线y=kx+b(k<0)上的两点,如果x1例2.已知点(-1,y1)、(4,y2)在一次函数y=3x-2的图像上,则y1、y2的大小关系是_________.
>
y1练习.已知一次函数
y
=(6+3m)x+(4-n).
(1)当m、n分别取何值时,y随x的增大而增大?
(2)当m、n分别取何值时,函数图像交y轴于负半轴?
(3)若函数图像不经过第一象限,求m、n的取值范围.
直线y=kx+b与直线y=kbx,它们在同一个坐标系中的图像大致为(
)
C
挑战自我
x
0
y
x
0
y
x
0
y
x
0
y
A
B
C
D
6.3
一次函数的图像(2)
像上山越走越高一样,有些一次函数的图像从左向右不断上升.
创设情境
像下山越走越低那样,有些一次函数的图像从左向右不断下降.
创设情境
观察这两个函数的图像,你有什么发现?
x的值越大,对应的y值也越大。
x的值越大,对应的y值越小。
1、你觉得是什么决定了这个函数图像会上升还是下降?
2、请你写一个一次函数并画出图像来支持或反驳上面的猜想。
探索活动1
(1)如果k>0,那么函数值y随自变量x增大而增大,图像经
过一、三象限;
在一次函数y=kx+b
中:
(2)如果k<0,那么函数值y随自变量x增大而减小,图像经
过二、四象限。
小结1
(1)y=-1.6
x+4,(2)y=0.5
x-5,
(3)y=4
x,(4)y=-
x-3,
(5)y=5
x-7.
已知函数:
y
值随
x
值增大而增大的函数是
;
(2)(3)(5)
从左往右,图像是下降的函数是
.
(1)(4)
3
2
请你写一个和y=4
x
的图像平行的一次函数
.
考考你
通过刚才的活动,我们发现一次函数y=kx+b中,k的符号、绝对值等等对函数图像有决定性的影响。
那么,一次函数表达式中b的值又对函数图像有什么影响呢?
研究一次函数
y1=2x
、y2=2x+3、
y3=2x-3
的关系。
0
x
y
y=2x
3
-3
y=2x+3
y=2x-3
探索活动2
你觉得这里的b对函数图像产生了什么影响?
x
y
0
y=kx(b=0)
一般地,正比例函数y=kx的图像是经过原点的一条直线.
如果b>0,那么一次函数y=kx+b的图像可以由正比例函数y=kx向上平移b个单位长度得到。
b>0,交y轴于正半轴
b<0,交y轴于负半轴
y=kx+b(b>0)
y=kx+b(b<0)
如果b<0,那么一次函数y=kx+b的图像可以由正比例函数y=kx向下平移|b|个单位长度得到。
(1)将一次函数y=2x-3的图像沿y轴向上平移8个单位长度,所得直线的函数表达式为(
)
A、y=2x-5
B、y=2x+5
C、y=2x+8
D、y=2x-8
(2)将直线y=x+b沿y轴向下平移3个单位长度,点A(1,2)落在平移后的直线上,则b的值为______.
4
B
考考你
一次函数
y=k
x+b
(
k、b为常数,且
k≠0)中k、
b
的值对函数图像的影响.
图像特征
大致图像
k>0
b>0
上升,
交y轴于正半轴.
b=0
上升,
交点在原点.
b<0
上升,
交y轴于负半轴.
x
y
0
x
y
0
x
y
0
归纳小结
一次函数
y=k
x+b
(
k、b为常数,且
k≠0)中k、
b
的值对函数图像的影响.
图像特征
大致图像
k<0
b>0
下降,
交y轴于正半轴.
b=0
下降,
交点在原点.
b<0
下降,
交y轴于负半轴.
x
y
0
x
y
0
x
y
0
归纳总结
归纳小结
例1.一次函数y=2x-3的图像经过(
)
A.第一、二、三象限.
B.第一、二、四象限.
C.第一、三、四象限.
D.第二、三、四象限.
C
例题与变式
变式1.一次函数y=ax+b
的图像经过第一、二、四象限,则一次函数y=bx+a的图像经过(
)
C
A.第一、二、三象限.
B.第一、二、四象限.
C.第一、三、四象限.
D.第二、三、四象限.
变式2.A(x1,y1)、B(x2,y2)是直线y=kx+b(k<0)上的两点,如果x1
>
y1
y
=(6+3m)x+(4-n).
(1)当m、n分别取何值时,y随x的增大而增大?
(2)当m、n分别取何值时,函数图像交y轴于负半轴?
(3)若函数图像不经过第一象限,求m、n的取值范围.
直线y=kx+b与直线y=kbx,它们在同一个坐标系中的图像大致为(
)
C
挑战自我
x
0
y
x
0
y
x
0
y
x
0
y
A
B
C
D
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
