勾股定理(一)
图片预览






文档简介
(共20张PPT)
1、探索直角三角形三边关系,掌握勾股定理的运用思维。
2、经历观察与发现直角三角形三边关系的过程,感受勾股定理的应用意识。
3、培养学生严谨的数学学习的态度,体会勾股定理的应用价值。
了解勾股之理的演绎过程,掌握勾股定理的应用。
理解勾股定理的推导过程。
通过拼图的办法来探索勾股定理的证明过程,理解内涵。
自主探究、合作交流、引导启发
这就是本届大会会徽的图案.
你见过这个图案吗?
你听说过勾股定理吗?
1、你曾见过这个图案吗
赵爽弦图
这个图案是3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称之为“赵爽弦图”
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
目前世界上许多科学家正在试图寻找其它星球的“人”,为此向宇宙发出了许多信号,如地球上人类的语言,音乐,各种图形等.我国数学家华罗庚建议,发射一种反映勾股定理的图形,如果宇宙人是“文明人”,那么他们一定会识别这种语言的.
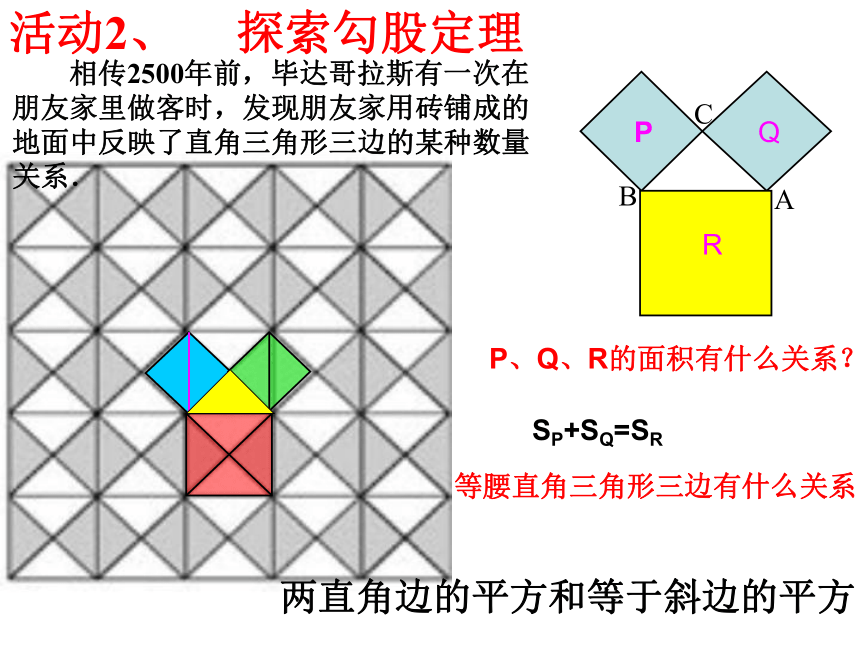
活动2、 探索勾股定理
P
Q
R
P、Q、R的面积有什么关系?
SP+SQ=SR
等腰直角三角形三边有什么关系?
两直角边的平方和等于斜边的平方
A
B
C
相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系.
对于等腰直角三角形有这样的性质:两直角边的平方和等于斜边的平方
那么对于一般的直角三角形是否也有这样的性质呢?
A
B
A
B
C
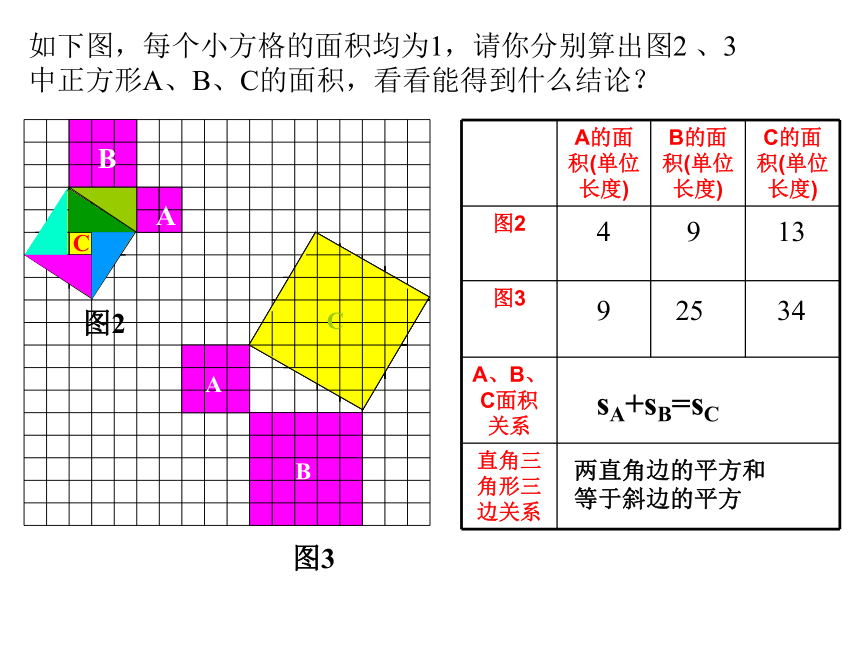
A的面积(单位长度) B的面积(单位长度) C的面积(单位长度)
图2
图3
A、B、C面积关系
直角三角形三边关系
图2
图3
4
9
13
9
25
34
sA+sB=sC
两直角边的平方和
等于斜边的平方
C
如下图,每个小方格的面积均为1,请你分别算出图2 、3中正方形A、B、C的面积,看看能得到什么结论?
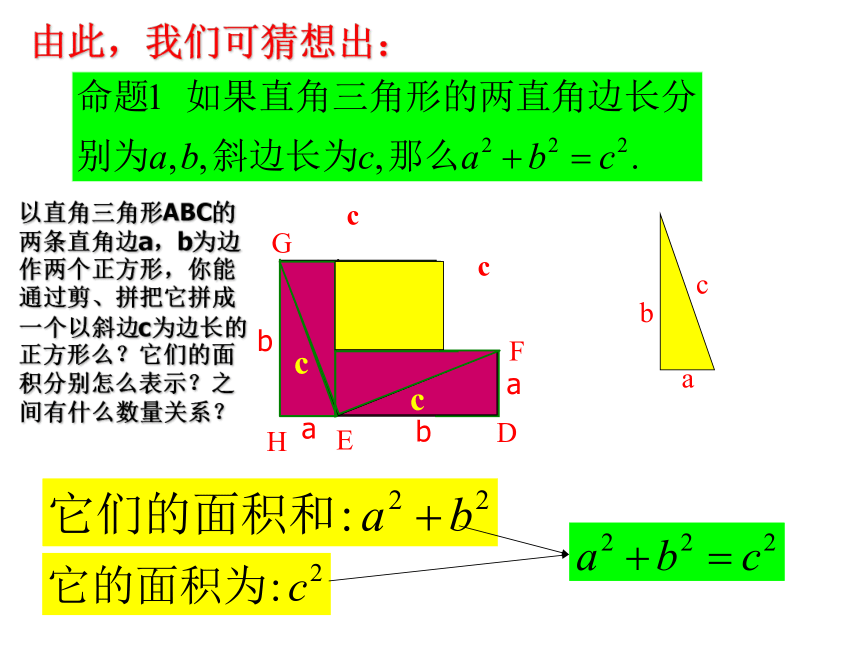
由此,我们可猜想出:
b
a
a
以直角三角形ABC的两条直角边a,b为边作两个正方形,你能通过剪、拼把它拼成一个以斜边c为边长的正方形么?它们的面积分别怎么表示?之间有什么数量关系?
c
c
c
c
b
E
D
F
G
H
a
b
c
a
b
c
①
②
③
④
⑤
青出
朱入
朱出
朱方
青方
青入
青入
青出
青出
华罗庚
青朱出入图
朱入
朱出
同学们,你能理解赵爽弦图的证明过程么?
a
b
c
b
c
a
大正方形面积:
还可看作四个直角三角形和一个小正方形之和:
即:
经过证明被确认正确的命题叫做定理.
E
F
G
H
I
J
K
L
“赵爽弦图’表现了我国古代人对数学的钻研精神和聪明才智,它是我国古代数学的骄傲,因此,这个图案被选为2002年在北京召开的国际数学家大会的会徽。
在西方,一般认为这个定理是毕达哥拉斯发现的,所以人们称这个定理为毕达哥拉斯定理。
以后我们要做更深入的研究!到底是谁最先发现勾股定理的,我们可以很自豪的说:“是我们中国,证据就是《周髀算经》”。
A
B
C
例1、蚂蚁沿图中的红色折线从A点爬到C点,一共爬了多少厘米?(小方格的边长为1厘米)
G
E
P
625
400
2
6
P的面积 =______________
X=____________
225
B
A
C
AB=__________
AC=__________
BC=__________
25
15
20
2、等边三角形的边长为12,
则它的高为______
3、在直角三角形中,如果有两边为3,4,那么另一边为_________
5或
A
B
C
D
1、 在直角三角形中,两条直角边分别为a,b, 斜边为c,则c2=____
a2+b2
6、一个长方形的长是宽的2 倍,其对角线的长是5㎝,那么它的宽是( )
A ㎝ B ㎝ C ㎝ D ㎝
4、如果直角三角形的一个锐角为30度,斜边长是 2 ,那么直角三角形的其它两边长是( )
A 1, B 1 ,3 C 1, D 1 ,5
5、如图,在RT△ABC中,∠C=90°,
∠B=45°,AC=1,则AB=( )
A 2 B 1 C D
A
C
B
A
B
C
翻开任何一部中国数学发展史,都不难发现,华夏祖先们每前进一步,都伴随着奋斗的汗水。中国数学起源于上古至西汉末期,中国数学的全盛时期是隋中叶至元后期。接下来在元后期至清中期,中国数学的发展缓慢。就在中国数学发展缓慢的时候,西方数学已大跨步超前,于是在中国数学发展史上出现了一个中西数学发展的合流期,这一时期约为公元1840年~1911年之间。近代数学的开端主要集中在公元1911年~1949年这一时期。尽管中国目前在世界数学的赛场上已处落后地位,然而,路遥识马力,今后鹿死谁手,仍未可知。
1、本节课我们经历了怎样的过程?
经历了从实际问题引入数学问题然后发现定理,再到探
索定理,最后学会验证定理及应用定理解决实际问题的过程。
2、本节课我们学到了什么?
通过本节课的学习我们不但知道了著名的勾股定理,还
知道从特殊到一般的探索方法及借助于图形的面积来探索、
验证数学结论的数形结合思想。
3、学了本节课后我们有什么感想?
很多的数学结论存在于平常的生活中,需要我们用数学
的眼光去观察、思考、发现,这节课我们还受到了数学文化
辉煌历史的教育。
1、P69-70第1、2题
2、通过书籍或网络查阅有关资料,了解勾股定理的历史背景和意义,了解更多的勾股定理证明方法。
1、探索直角三角形三边关系,掌握勾股定理的运用思维。
2、经历观察与发现直角三角形三边关系的过程,感受勾股定理的应用意识。
3、培养学生严谨的数学学习的态度,体会勾股定理的应用价值。
了解勾股之理的演绎过程,掌握勾股定理的应用。
理解勾股定理的推导过程。
通过拼图的办法来探索勾股定理的证明过程,理解内涵。
自主探究、合作交流、引导启发
这就是本届大会会徽的图案.
你见过这个图案吗?
你听说过勾股定理吗?
1、你曾见过这个图案吗
赵爽弦图
这个图案是3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称之为“赵爽弦图”
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
目前世界上许多科学家正在试图寻找其它星球的“人”,为此向宇宙发出了许多信号,如地球上人类的语言,音乐,各种图形等.我国数学家华罗庚建议,发射一种反映勾股定理的图形,如果宇宙人是“文明人”,那么他们一定会识别这种语言的.
活动2、 探索勾股定理
P
Q
R
P、Q、R的面积有什么关系?
SP+SQ=SR
等腰直角三角形三边有什么关系?
两直角边的平方和等于斜边的平方
A
B
C
相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系.
对于等腰直角三角形有这样的性质:两直角边的平方和等于斜边的平方
那么对于一般的直角三角形是否也有这样的性质呢?
A
B
A
B
C
A的面积(单位长度) B的面积(单位长度) C的面积(单位长度)
图2
图3
A、B、C面积关系
直角三角形三边关系
图2
图3
4
9
13
9
25
34
sA+sB=sC
两直角边的平方和
等于斜边的平方
C
如下图,每个小方格的面积均为1,请你分别算出图2 、3中正方形A、B、C的面积,看看能得到什么结论?
由此,我们可猜想出:
b
a
a
以直角三角形ABC的两条直角边a,b为边作两个正方形,你能通过剪、拼把它拼成一个以斜边c为边长的正方形么?它们的面积分别怎么表示?之间有什么数量关系?
c
c
c
c
b
E
D
F
G
H
a
b
c
a
b
c
①
②
③
④
⑤
青出
朱入
朱出
朱方
青方
青入
青入
青出
青出
华罗庚
青朱出入图
朱入
朱出
同学们,你能理解赵爽弦图的证明过程么?
a
b
c
b
c
a
大正方形面积:
还可看作四个直角三角形和一个小正方形之和:
即:
经过证明被确认正确的命题叫做定理.
E
F
G
H
I
J
K
L
“赵爽弦图’表现了我国古代人对数学的钻研精神和聪明才智,它是我国古代数学的骄傲,因此,这个图案被选为2002年在北京召开的国际数学家大会的会徽。
在西方,一般认为这个定理是毕达哥拉斯发现的,所以人们称这个定理为毕达哥拉斯定理。
以后我们要做更深入的研究!到底是谁最先发现勾股定理的,我们可以很自豪的说:“是我们中国,证据就是《周髀算经》”。
A
B
C
例1、蚂蚁沿图中的红色折线从A点爬到C点,一共爬了多少厘米?(小方格的边长为1厘米)
G
E
P
625
400
2
6
P的面积 =______________
X=____________
225
B
A
C
AB=__________
AC=__________
BC=__________
25
15
20
2、等边三角形的边长为12,
则它的高为______
3、在直角三角形中,如果有两边为3,4,那么另一边为_________
5或
A
B
C
D
1、 在直角三角形中,两条直角边分别为a,b, 斜边为c,则c2=____
a2+b2
6、一个长方形的长是宽的2 倍,其对角线的长是5㎝,那么它的宽是( )
A ㎝ B ㎝ C ㎝ D ㎝
4、如果直角三角形的一个锐角为30度,斜边长是 2 ,那么直角三角形的其它两边长是( )
A 1, B 1 ,3 C 1, D 1 ,5
5、如图,在RT△ABC中,∠C=90°,
∠B=45°,AC=1,则AB=( )
A 2 B 1 C D
A
C
B
A
B
C
翻开任何一部中国数学发展史,都不难发现,华夏祖先们每前进一步,都伴随着奋斗的汗水。中国数学起源于上古至西汉末期,中国数学的全盛时期是隋中叶至元后期。接下来在元后期至清中期,中国数学的发展缓慢。就在中国数学发展缓慢的时候,西方数学已大跨步超前,于是在中国数学发展史上出现了一个中西数学发展的合流期,这一时期约为公元1840年~1911年之间。近代数学的开端主要集中在公元1911年~1949年这一时期。尽管中国目前在世界数学的赛场上已处落后地位,然而,路遥识马力,今后鹿死谁手,仍未可知。
1、本节课我们经历了怎样的过程?
经历了从实际问题引入数学问题然后发现定理,再到探
索定理,最后学会验证定理及应用定理解决实际问题的过程。
2、本节课我们学到了什么?
通过本节课的学习我们不但知道了著名的勾股定理,还
知道从特殊到一般的探索方法及借助于图形的面积来探索、
验证数学结论的数形结合思想。
3、学了本节课后我们有什么感想?
很多的数学结论存在于平常的生活中,需要我们用数学
的眼光去观察、思考、发现,这节课我们还受到了数学文化
辉煌历史的教育。
1、P69-70第1、2题
2、通过书籍或网络查阅有关资料,了解勾股定理的历史背景和意义,了解更多的勾股定理证明方法。
