6.3.2一次函数的图像 苏科版数学八年级上册课件(21张)
文档属性
| 名称 | 6.3.2一次函数的图像 苏科版数学八年级上册课件(21张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-09 08:40:19 | ||
图片预览




文档简介
(共21张PPT)
5.3
一次函数图象
(2)
苏教版数学八年级上册
复
习
引
入
1.一次函数的图像是一条直线,所以画一次函数的
图像要先确定两个点,这两个点通常是哪两个点呢?
一般情况下,应找出直线与坐标轴的两个交点
2.直线y=2x+4
与x轴的交点是
;
与y轴的交点是
。
直线
与x轴的交点是
;
与y轴的交点是
。
直线y=kx+b(k≠0)与x轴的交点是
;
与y轴的交点是
。
(-2,0)
(0,4)
(-2,0)
(0,-3)
(0,b)
在坐标系中画出一次函数y=2x+4
,
的图像
探
究
活
动
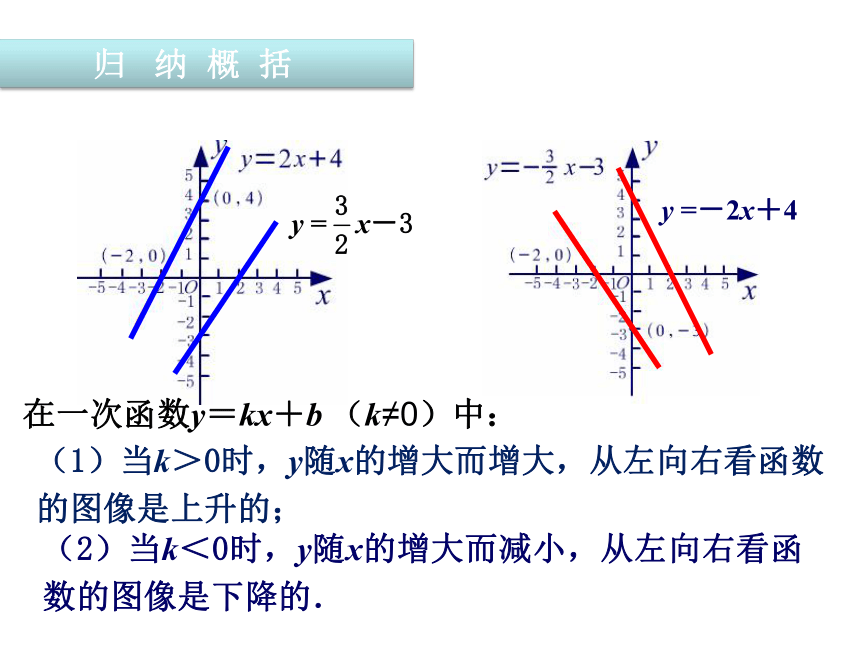
观察这两个函数的图像,回答以下几个问题
y
=-2x+4
(1)当k>0时,y随x的增大而增大,从左向右看函数的图像是上升的;
(2)当k<0时,y随x的增大而减小,从左向右看函数的图像是下降的.
在一次函数y=kx+b
(k≠0)中:
归
纳
概
括
y
= x-3
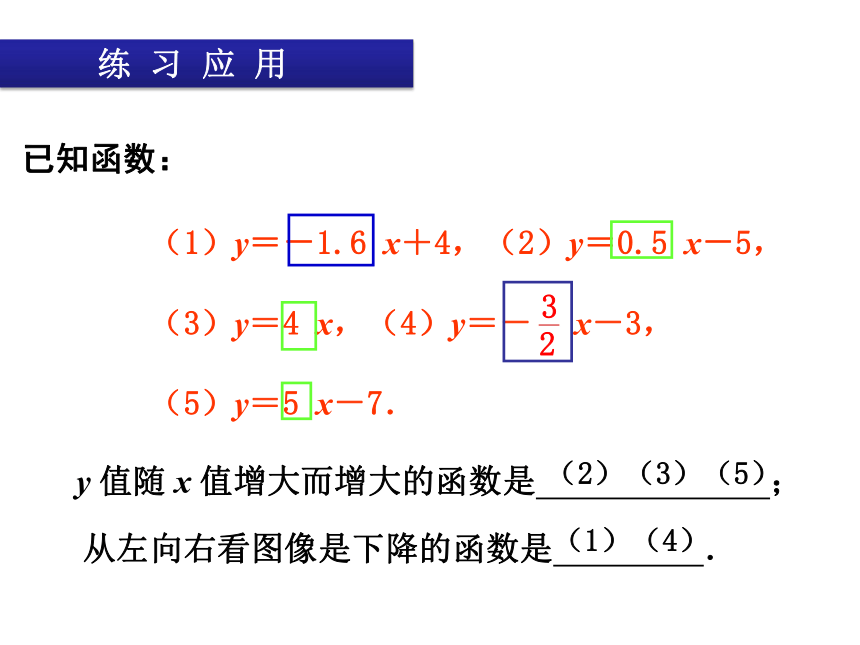
(1)y=-1.6
x+4,(2)y=0.5
x-5,
(3)y=4
x,(4)y=-
x-3,
(5)y=5
x-7.
已知函数:
y
值随
x
值增大而增大的函数是
;
(2)(3)(5)
从左向右看图像是下降的函数是
.
(1)(4)
练
习
应
用
3
2
x
-2
-1
0
1
2
…
y1=2x
-4
-2
0
2
4
…
y2=2x+3
-1
1
3
5
7
…
y3=2x-3
-7
-5
-3
-1
1
…
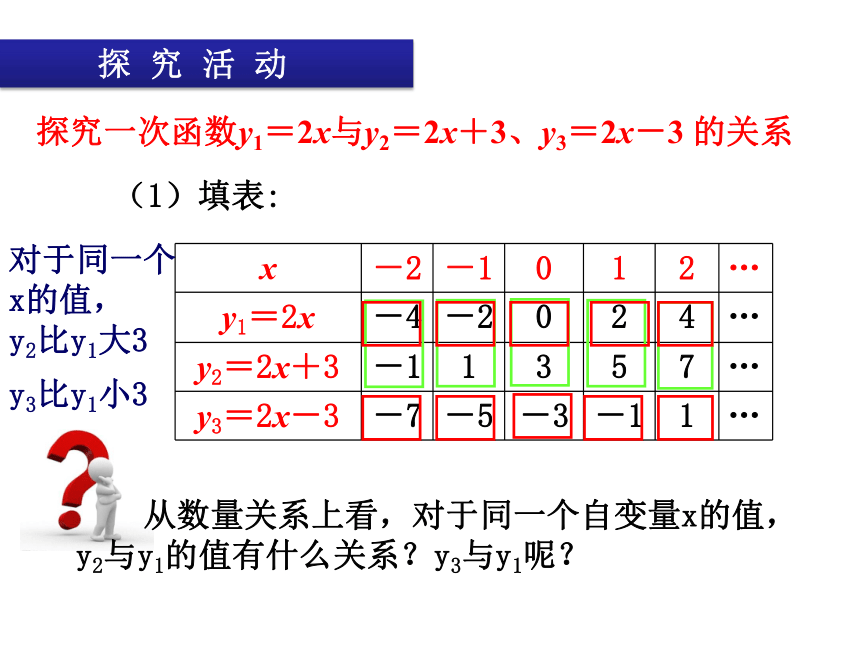
(1)填表:
从数量关系上看,对于同一个自变量x的值,y2与y1的值有什么关系?y3与y1呢?
探
究
活
动
探究一次函数y1=2x与y2=2x+3、y3=2x-3
的关系
对于同一个
x的值,
y2比y1大3
y3比y1小3
探
究
活
动
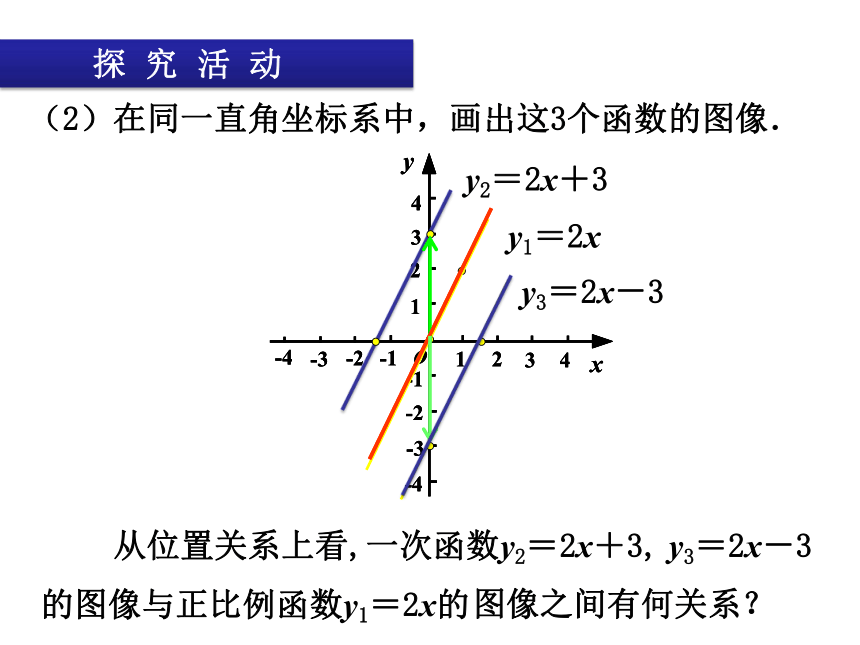
(2)在同一直角坐标系中,画出这3个函数的图像.
y3=2x-3
y1=2x
y2=2x+3
从位置关系上看,一次函数y2=2x+3,
y3=2x-3
的图像与正比例函数y1=2x的
图像之间有何关系?
归
纳
概
括
一次函数y=kx+b(k≠0)的图像可以由正比例
函数y=kx(k≠0)_______得到
平移
(1)一次函数
y=k
x+b(
b>0)的图像是由正比例函数y=k
x的图像沿y
轴向__平移__个单位长度得到的一条直线.
(2)一次函数y=k
x+b(
b<0)的图像是由正比例函数y=k
x的图像沿
y
轴向__平移__个单位长度得到的一条直线.
上
b
下
|b|
探
索
发
现
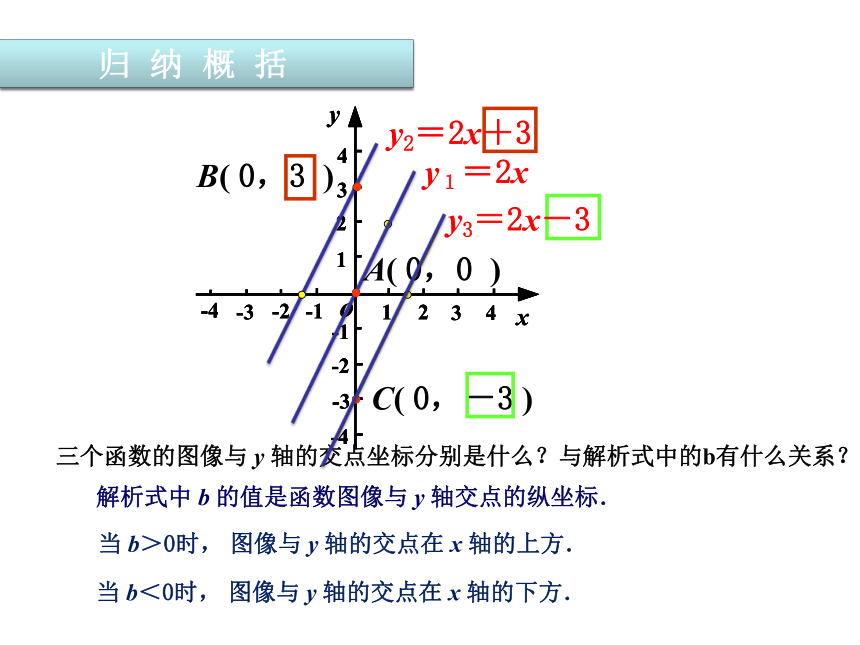
三个函数的图像与
y
轴的交点坐标分别是什么?与解析式中的b有什么关系?
A(
0,0
)
B(
0,3
)
C(
0,-3
)
解析式中
b
的值是函数图像与
y
轴交点的纵坐标.
y3=2x-3
y2=2x+3
y1=2x
当
b>0时,
图像与
y
轴的交点在
x
轴的上方.
当
b<0时,
图像与
y
轴的交点在
x
轴的下方.
归
纳
概
括
练
习
应
用
你能利用函数y=2x+3的图像画出函数y=2x-3
的图像吗?反过来呢?
y=2x+3
的图像
y=2x-3
的图像
沿
y轴向上平移6个单位长度
沿
y轴向下平移6个单位长度
y=2x
一次函数
y=k
x+b
(
k、b为常数,且
k≠0)中k、
b
的值对函数图像的影响.
图像经过的象限
图像特征
k>0
x
y
0
x
y
0
x
y
0
归
纳
概
括
一,二,三象限
一,三象限
一,三,四象限
y随x的增大而增大;
从左向右看函数图像是上升的
大致图像
b>0
b
=
0
b
<
0
一次函数
y=k
x+b
(
k、b为常数,且
k≠0)中k、
b
的值对函数图像的影响.
图像经过的象限
图像特征
k<0
x
y
0
x
y
0
x
y
0
归
纳
概
括
一,二,四象限
二,四象限
二,三,四象限
y随x的增大而减小;
从左向右看函数图像是下降的
大致图像
b>0
b
=
0
b
<
0
例1.已知一次函数y
=(2k-1)x+3k+2.
(1)当k=_____时,直线经过原点.
(3)当k
时,与
y
轴的交点在
x
轴的上方.
(2)当k______时,y
随
x
的增大而增大.
(4)当k满足
时,它的图像经过
一、二、四象限.
例
题
分
析
>
>
且k≠
例
题
分
析
例2.
(1)直线y=2x+1向上平移2个单位得直线_______;
向下平移2个单位得直线______;
(2)直线y=-4x+1是由直线________向上平移3单
位得到的;
(3)已知直线y=kx-1向下平移2个单位后经过点(1,1),则k=______。
y=2x+3
y=2x-1
y=-4x-2
4
(4)已知直线y1=kx+b经过点(1,2)且与直线
y2=-x+1平行,则k=____;b=
-1
3
例
题
分
析
例3、一次函数y=2
x+4的图像如图所示.
(1)当x为何值时,y=0?
(2)当x为何值时,y
<0?
(3)当x为何值时,y
>
0?
x=-2
x<-2
x>-2
1.一次函数y=2x-3的图像经过(
)
A.第一、二、三象限.
B.第一、二、四象限.
C.第一、三、四象限.
D.第二、三、四象限.
练
习
应
用
C
2.根据图像确定一次函数y=kx+b(k≠0)中k,b的符号。
练
习
应
用
x
y
o
x
x
y
y
o
o
k>0
b>0
k<0
b<0
k>0
b=0
练
习
应
用
3.
一次函数y=k
x+b
(k≠0)的图像如图所示.
(1)求函数关系式.
(2)观察图像
当x为何值时,y
>
0
?
当x为何值时,y
<
0
?
y=-x-3
x<-3
x>-3
应
用
提
高
4.一次函数y=kx+b
(k≠0)中,kb>0,且y随x的增大而减小,则它的图像大致为(
)
D
C
B
A
x
y
o
x
x
x
y
y
y
o
o
o
C
5.3
一次函数图象
(2)
苏教版数学八年级上册
复
习
引
入
1.一次函数的图像是一条直线,所以画一次函数的
图像要先确定两个点,这两个点通常是哪两个点呢?
一般情况下,应找出直线与坐标轴的两个交点
2.直线y=2x+4
与x轴的交点是
;
与y轴的交点是
。
直线
与x轴的交点是
;
与y轴的交点是
。
直线y=kx+b(k≠0)与x轴的交点是
;
与y轴的交点是
。
(-2,0)
(0,4)
(-2,0)
(0,-3)
(0,b)
在坐标系中画出一次函数y=2x+4
,
的图像
探
究
活
动
观察这两个函数的图像,回答以下几个问题
y
=-2x+4
(1)当k>0时,y随x的增大而增大,从左向右看函数的图像是上升的;
(2)当k<0时,y随x的增大而减小,从左向右看函数的图像是下降的.
在一次函数y=kx+b
(k≠0)中:
归
纳
概
括
y
= x-3
(1)y=-1.6
x+4,(2)y=0.5
x-5,
(3)y=4
x,(4)y=-
x-3,
(5)y=5
x-7.
已知函数:
y
值随
x
值增大而增大的函数是
;
(2)(3)(5)
从左向右看图像是下降的函数是
.
(1)(4)
练
习
应
用
3
2
x
-2
-1
0
1
2
…
y1=2x
-4
-2
0
2
4
…
y2=2x+3
-1
1
3
5
7
…
y3=2x-3
-7
-5
-3
-1
1
…
(1)填表:
从数量关系上看,对于同一个自变量x的值,y2与y1的值有什么关系?y3与y1呢?
探
究
活
动
探究一次函数y1=2x与y2=2x+3、y3=2x-3
的关系
对于同一个
x的值,
y2比y1大3
y3比y1小3
探
究
活
动
(2)在同一直角坐标系中,画出这3个函数的图像.
y3=2x-3
y1=2x
y2=2x+3
从位置关系上看,一次函数y2=2x+3,
y3=2x-3
的图像与正比例函数y1=2x的
图像之间有何关系?
归
纳
概
括
一次函数y=kx+b(k≠0)的图像可以由正比例
函数y=kx(k≠0)_______得到
平移
(1)一次函数
y=k
x+b(
b>0)的图像是由正比例函数y=k
x的图像沿y
轴向__平移__个单位长度得到的一条直线.
(2)一次函数y=k
x+b(
b<0)的图像是由正比例函数y=k
x的图像沿
y
轴向__平移__个单位长度得到的一条直线.
上
b
下
|b|
探
索
发
现
三个函数的图像与
y
轴的交点坐标分别是什么?与解析式中的b有什么关系?
A(
0,0
)
B(
0,3
)
C(
0,-3
)
解析式中
b
的值是函数图像与
y
轴交点的纵坐标.
y3=2x-3
y2=2x+3
y1=2x
当
b>0时,
图像与
y
轴的交点在
x
轴的上方.
当
b<0时,
图像与
y
轴的交点在
x
轴的下方.
归
纳
概
括
练
习
应
用
你能利用函数y=2x+3的图像画出函数y=2x-3
的图像吗?反过来呢?
y=2x+3
的图像
y=2x-3
的图像
沿
y轴向上平移6个单位长度
沿
y轴向下平移6个单位长度
y=2x
一次函数
y=k
x+b
(
k、b为常数,且
k≠0)中k、
b
的值对函数图像的影响.
图像经过的象限
图像特征
k>0
x
y
0
x
y
0
x
y
0
归
纳
概
括
一,二,三象限
一,三象限
一,三,四象限
y随x的增大而增大;
从左向右看函数图像是上升的
大致图像
b>0
b
=
0
b
<
0
一次函数
y=k
x+b
(
k、b为常数,且
k≠0)中k、
b
的值对函数图像的影响.
图像经过的象限
图像特征
k<0
x
y
0
x
y
0
x
y
0
归
纳
概
括
一,二,四象限
二,四象限
二,三,四象限
y随x的增大而减小;
从左向右看函数图像是下降的
大致图像
b>0
b
=
0
b
<
0
例1.已知一次函数y
=(2k-1)x+3k+2.
(1)当k=_____时,直线经过原点.
(3)当k
时,与
y
轴的交点在
x
轴的上方.
(2)当k______时,y
随
x
的增大而增大.
(4)当k满足
时,它的图像经过
一、二、四象限.
例
题
分
析
>
>
且k≠
例
题
分
析
例2.
(1)直线y=2x+1向上平移2个单位得直线_______;
向下平移2个单位得直线______;
(2)直线y=-4x+1是由直线________向上平移3单
位得到的;
(3)已知直线y=kx-1向下平移2个单位后经过点(1,1),则k=______。
y=2x+3
y=2x-1
y=-4x-2
4
(4)已知直线y1=kx+b经过点(1,2)且与直线
y2=-x+1平行,则k=____;b=
-1
3
例
题
分
析
例3、一次函数y=2
x+4的图像如图所示.
(1)当x为何值时,y=0?
(2)当x为何值时,y
<0?
(3)当x为何值时,y
>
0?
x=-2
x<-2
x>-2
1.一次函数y=2x-3的图像经过(
)
A.第一、二、三象限.
B.第一、二、四象限.
C.第一、三、四象限.
D.第二、三、四象限.
练
习
应
用
C
2.根据图像确定一次函数y=kx+b(k≠0)中k,b的符号。
练
习
应
用
x
y
o
x
x
y
y
o
o
k>0
b>0
k<0
b<0
k>0
b=0
练
习
应
用
3.
一次函数y=k
x+b
(k≠0)的图像如图所示.
(1)求函数关系式.
(2)观察图像
当x为何值时,y
>
0
?
当x为何值时,y
<
0
?
y=-x-3
x<-3
x>-3
应
用
提
高
4.一次函数y=kx+b
(k≠0)中,kb>0,且y随x的增大而减小,则它的图像大致为(
)
D
C
B
A
x
y
o
x
x
x
y
y
y
o
o
o
C
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
