6.4.1用一次函数解决问题 苏科版数学八年级上册课件(22张)
文档属性
| 名称 | 6.4.1用一次函数解决问题 苏科版数学八年级上册课件(22张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-09 08:40:23 | ||
图片预览






文档简介
(共22张PPT)
与
名闻遐迩的玉龙雪山,位于云南省丽江城北15km,由12座山峰组成,主峰海拔5596m,海拔4500m处远远望去,一条黑白分明的雪线蜿蜒山头,雪线以上是银光闪烁的冰雪世界,雪线以下是草木葱葱的原始森林.
由于气候变暖等原因,2002~2007年间,玉龙雪山的雪线平均每年约上升10m,假如按此速度推算,经过几年,玉龙雪山的雪线将由现在的4500m退至山顶而消失?
1.从这段文字中,获得了哪些数量的信息?
名闻遐迩的玉龙雪山,位于云南省丽江城北15km,由12座山峰组成,主峰海拔5596m,海拔4500m处远远望去,一条黑白分明的雪线蜿蜒山头,雪线以上是银光闪烁的冰雪世界,雪线以下是草木葱葱的原始森林.
2.这些数量之间有什么关系?
5596
4500
数年后
雪线海拔
4500m
数年内雪线上升总高度
常量
变量
探寻数量关系:
如何解决这个问题?
由于气候变暖等原因,2002~2007年间,玉龙雪山的雪线平均每年约上升10m,假如按此速度推算,经过几年,玉龙雪山的雪线将由现在的4500m退至山顶而消失?
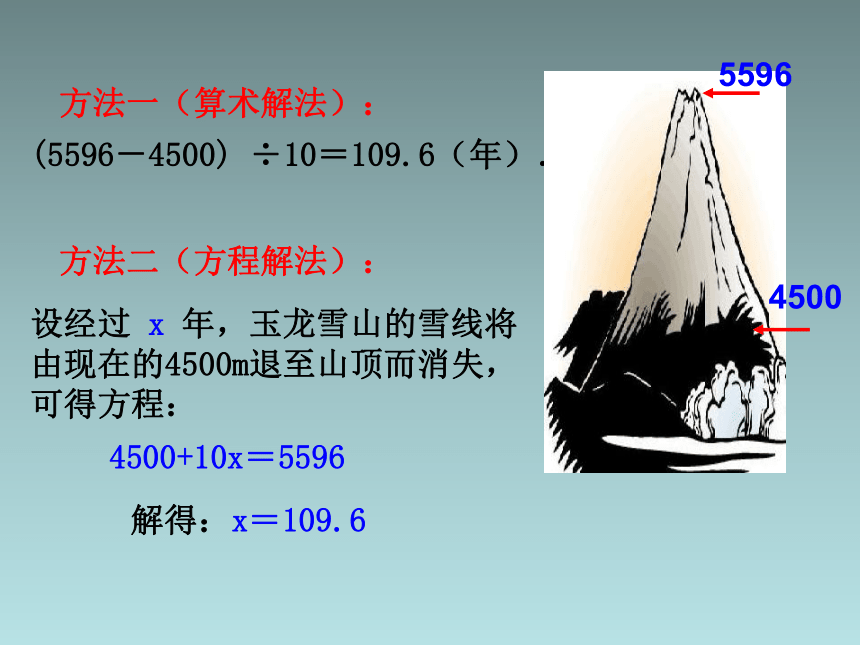
方法一(算术解法):
(5596-4500)
÷10=109.6(年).
方法二(方程解法):
设经过
x
年,玉龙雪山的雪线将由现在的4500m退至山顶而消失,可得方程:
4500+10x=5596
解得:x=109.6
5596
4500
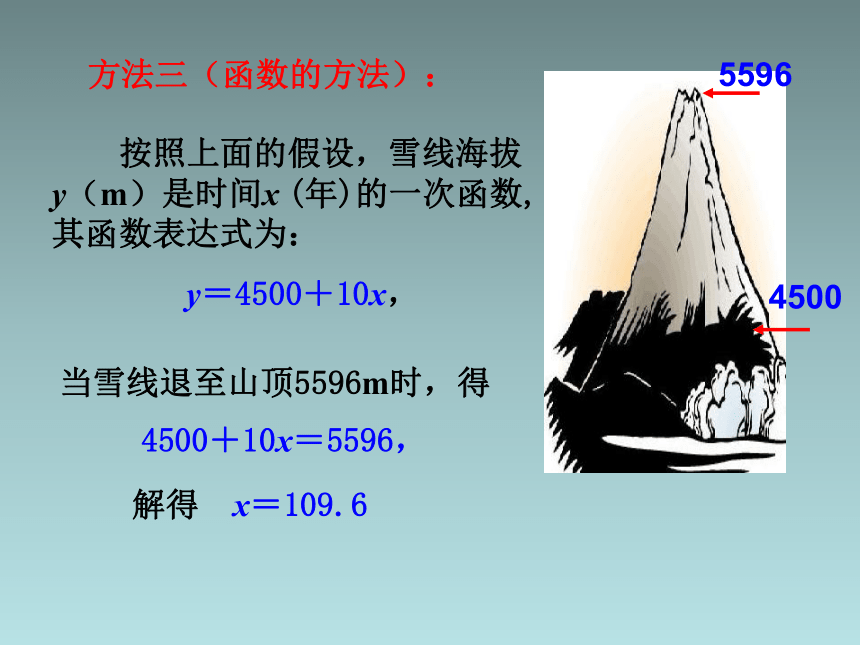
方法三(函数的方法):
按照上面的假设,雪线海拔
y(m)是时间x
(年)的一次函数,其函数表达式为:
y=4500+10x,
当雪线退至山顶5596m时,得
4500+10x=5596,
解得 x=109.6
5596
4500
实际问题
表
示
(变量与变量之间的关系)
一次函数
解
决
问题1
某工厂生产某种产品,已知该工厂正常运转的固定成本为每天12000元,生产该产品的原料成本为每件900元.
(1)
写出每天的生产成本(包括固定成本和原料成本)与产量之间的函数表达式;
每天的
生产成本
数量关系:
固定成本
原料成本
常量
变量
每天的
生产成本
仔细审题,寻找数量关系!
问题1
某工厂生产某种产品,已知该工厂正常运转的固定成本为每天12000元,生产该产品的原料成本为每件900元.
(1)
写出每天的生产成本(包括固定成本和原料成本)与产量之间的函数表达式;
y1=900x+12000.
解:每天的生产成本y1(元)与产量x(件)之间的函数表达式是:
根据数量关系,列函数表达式!
问题1
某工厂生产某种产品,已知该工厂正常运转的固定成本为每天12000元,生产该产品的原料成本为每件900元.
(2)
如果每件产品的出厂价为1200元,那么每天生产多少件产品,该工厂才有赢利?
y2=1200x.
解:每天的销售收入y2(元)与
产量x
(件)之间的函数表达式是:
每天的销售收入
>
生产成本
问题1
某工厂生产某种产品,已知该工厂正常运转的固定成本为每天12000元,生产该产品的原料成本为每件900元.
(2)
如果每件产品的出厂价为1200元,那么每天生产多少件产品,该工厂才有赢利?
y2=1200x.
解:每天的销售收入y2(元)与
产量x
(件)之间的函数表达式是:
当销售收入y2大于生产成本y1时,工厂有赢利,即
1200x>900x+12000.
解得 x
>40.
答:每天生产的产品超过40件,该工厂才会有赢利。
【交流】问题2
在人才招聘会上,某公司承诺:应聘者被录用后第
1
年的月工资为
2
000元,在以后的一段时间内,每年的月工资比上一年的月工资增加
300元.
(1)某人在该公司连续工作n年,写出他第n年的月工资
y与n的函数表达式.
解:他第
n
年的月工资
y与n的函数表达式是:
y=300(n-1)+2000.
仔细审题,寻找数量关系!
根据数量关系,列函数表达式!
(2)他第
5
年的年收入能否超过40
000元?
解:当
n=5
时,y=
300×(5-1)+2000
=3200(元)
∴第
5
年的月工资为3200元
∴年收入为:3200×12=38400(元)
<40000(元)
∴他第5年的年收入不能超过40000元.
已知一变量,求另一变量的值
(1)某人在该公司连续工作n年,写出他第n年的月工资
y与n的函数表达式.
解:他第
n
年的月工资
y与n的函数表达式是:
y=300(n-1)+2000.
转化
(一次函数)
解决
实际问题
数学模型
用一次函数解决问题
(1)分析数量关系
(2)根据数量关系,列出一次函数表达式
(3)已知一个变量,求另一个变量的值或范围
具体过程:
【练习】某市出租车收费标准:不超过3千米计费为7.0元,3千米后按2.4元/千米计费.
(1)当路程表显示2km时,应付费多少元?
(2)当路程表显示7km时,应付费多少元?
解:应付费7元。
解:7.0+2.4×(7-3)=16.6(元)
∴应付费16.6元。
【练习】某市出租车收费标准:不超过3千米计费为7.0元,3千米后按2.4元/千米计费.
(3)写出车费
y
(元)与路程
x
(千米)之间的函数表达式;
解:当
0时,
y=7
当
x>3
时,
y=7+2.4(x-3)
注意一次函数自变量的取值范围要与实际问题相符!
【练习】某市出租车收费标准:不超过3千米计费为7.0元,3千米后按2.4元/千米计费.
(4)小亮乘出租车出行,付费19元,计算小亮乘车的路程.
(3)写出车费
y
(元)与路程
x
(千米)之间的函数表达式;
解:当
0时,
y=7
当
x>3
时,
y=7+2.4(x-3)
解:∵19>7
∴乘车路程>3km
∴当y=19时,19=7+2.4(x-3)
解得:x=8
∴小亮的乘车路程为8km。
【拓展提高】1.
如图,公路上有A、B、C三个汽车站,一辆汽车8:00从离A站10km处的P地出发,向C站匀速行驶,15min后离A站30km
(1)设出发x
h后,汽车离A站y
km,写出
y与
x之间的函数表达式
(2)当汽车行驶到离A站250km的B站时,接到通知要在12:00前赶到离B站60km的C站。汽车按原速行驶,能否准时到达?如果能,那么汽车何时到达C站?
A
P
B
C
【拓展提高】2.某技工培训中心有钳工20名、车工30名。现将这50名技工派往A、B两地工作,两地技工的月工资情况如下:
钳工(元/月)
车工(元/月)
A地
1800
1600
B地
1600
1200
(1)若派往A地
x
名钳工,余下的技工全部派往B地,写出这50名技工的月工资总额
y(元)与
x
之间的函数表达式,并写出x的取值范围。
(2)若派往A地
x
名车工,余下的技工全部派往B地,写出这50名技工的月工资总额
y(元)与
x
之间的函数表达式,并写出x的取值范围。
【拓展提高】某技工培训中心有钳工20名、车工30名。现将这50名技工派往A、B两地工作,两地技工的月工资情况如下:
钳工(元/月)
车工(元/月)
A地
1800
1600
B地
1600
1200
(1)若派往A地
x
名钳工,余下的技工全部派往B地,写出这50名技工的月工资总额
y(元)与
x
之间的函数表达式,并写出x的取值范围。
B地
20名钳工
30名车工
A地
x
20-x
30
【拓展提高】某技工培训中心有钳工20名、车工30名。现将这50名技工派往A、B两地工作,两地技工的月工资情况如下:
钳工(元/月)
车工(元/月)
A地
1800
1600
B地
1600
1200
(2)若派往A地
x
名车工,余下的技工全部派往B地,写出这50名技工的月工资总额
y(元)与
x
之间的函数表达式,并写出x的取值范围。
B地
20名钳工
30名车工
A地
30-x
x
20
转化
(一次函数)
解决
实际问题
数学模型
【小结】
通过这节课的学习,你学习到什么新知识?获得了什么经验?还有什么疑问?
【作业】教科书P159习题6.4——1、2、4.
与
名闻遐迩的玉龙雪山,位于云南省丽江城北15km,由12座山峰组成,主峰海拔5596m,海拔4500m处远远望去,一条黑白分明的雪线蜿蜒山头,雪线以上是银光闪烁的冰雪世界,雪线以下是草木葱葱的原始森林.
由于气候变暖等原因,2002~2007年间,玉龙雪山的雪线平均每年约上升10m,假如按此速度推算,经过几年,玉龙雪山的雪线将由现在的4500m退至山顶而消失?
1.从这段文字中,获得了哪些数量的信息?
名闻遐迩的玉龙雪山,位于云南省丽江城北15km,由12座山峰组成,主峰海拔5596m,海拔4500m处远远望去,一条黑白分明的雪线蜿蜒山头,雪线以上是银光闪烁的冰雪世界,雪线以下是草木葱葱的原始森林.
2.这些数量之间有什么关系?
5596
4500
数年后
雪线海拔
4500m
数年内雪线上升总高度
常量
变量
探寻数量关系:
如何解决这个问题?
由于气候变暖等原因,2002~2007年间,玉龙雪山的雪线平均每年约上升10m,假如按此速度推算,经过几年,玉龙雪山的雪线将由现在的4500m退至山顶而消失?
方法一(算术解法):
(5596-4500)
÷10=109.6(年).
方法二(方程解法):
设经过
x
年,玉龙雪山的雪线将由现在的4500m退至山顶而消失,可得方程:
4500+10x=5596
解得:x=109.6
5596
4500
方法三(函数的方法):
按照上面的假设,雪线海拔
y(m)是时间x
(年)的一次函数,其函数表达式为:
y=4500+10x,
当雪线退至山顶5596m时,得
4500+10x=5596,
解得 x=109.6
5596
4500
实际问题
表
示
(变量与变量之间的关系)
一次函数
解
决
问题1
某工厂生产某种产品,已知该工厂正常运转的固定成本为每天12000元,生产该产品的原料成本为每件900元.
(1)
写出每天的生产成本(包括固定成本和原料成本)与产量之间的函数表达式;
每天的
生产成本
数量关系:
固定成本
原料成本
常量
变量
每天的
生产成本
仔细审题,寻找数量关系!
问题1
某工厂生产某种产品,已知该工厂正常运转的固定成本为每天12000元,生产该产品的原料成本为每件900元.
(1)
写出每天的生产成本(包括固定成本和原料成本)与产量之间的函数表达式;
y1=900x+12000.
解:每天的生产成本y1(元)与产量x(件)之间的函数表达式是:
根据数量关系,列函数表达式!
问题1
某工厂生产某种产品,已知该工厂正常运转的固定成本为每天12000元,生产该产品的原料成本为每件900元.
(2)
如果每件产品的出厂价为1200元,那么每天生产多少件产品,该工厂才有赢利?
y2=1200x.
解:每天的销售收入y2(元)与
产量x
(件)之间的函数表达式是:
每天的销售收入
>
生产成本
问题1
某工厂生产某种产品,已知该工厂正常运转的固定成本为每天12000元,生产该产品的原料成本为每件900元.
(2)
如果每件产品的出厂价为1200元,那么每天生产多少件产品,该工厂才有赢利?
y2=1200x.
解:每天的销售收入y2(元)与
产量x
(件)之间的函数表达式是:
当销售收入y2大于生产成本y1时,工厂有赢利,即
1200x>900x+12000.
解得 x
>40.
答:每天生产的产品超过40件,该工厂才会有赢利。
【交流】问题2
在人才招聘会上,某公司承诺:应聘者被录用后第
1
年的月工资为
2
000元,在以后的一段时间内,每年的月工资比上一年的月工资增加
300元.
(1)某人在该公司连续工作n年,写出他第n年的月工资
y与n的函数表达式.
解:他第
n
年的月工资
y与n的函数表达式是:
y=300(n-1)+2000.
仔细审题,寻找数量关系!
根据数量关系,列函数表达式!
(2)他第
5
年的年收入能否超过40
000元?
解:当
n=5
时,y=
300×(5-1)+2000
=3200(元)
∴第
5
年的月工资为3200元
∴年收入为:3200×12=38400(元)
<40000(元)
∴他第5年的年收入不能超过40000元.
已知一变量,求另一变量的值
(1)某人在该公司连续工作n年,写出他第n年的月工资
y与n的函数表达式.
解:他第
n
年的月工资
y与n的函数表达式是:
y=300(n-1)+2000.
转化
(一次函数)
解决
实际问题
数学模型
用一次函数解决问题
(1)分析数量关系
(2)根据数量关系,列出一次函数表达式
(3)已知一个变量,求另一个变量的值或范围
具体过程:
【练习】某市出租车收费标准:不超过3千米计费为7.0元,3千米后按2.4元/千米计费.
(1)当路程表显示2km时,应付费多少元?
(2)当路程表显示7km时,应付费多少元?
解:应付费7元。
解:7.0+2.4×(7-3)=16.6(元)
∴应付费16.6元。
【练习】某市出租车收费标准:不超过3千米计费为7.0元,3千米后按2.4元/千米计费.
(3)写出车费
y
(元)与路程
x
(千米)之间的函数表达式;
解:当
0
y=7
当
x>3
时,
y=7+2.4(x-3)
注意一次函数自变量的取值范围要与实际问题相符!
【练习】某市出租车收费标准:不超过3千米计费为7.0元,3千米后按2.4元/千米计费.
(4)小亮乘出租车出行,付费19元,计算小亮乘车的路程.
(3)写出车费
y
(元)与路程
x
(千米)之间的函数表达式;
解:当
0
y=7
当
x>3
时,
y=7+2.4(x-3)
解:∵19>7
∴乘车路程>3km
∴当y=19时,19=7+2.4(x-3)
解得:x=8
∴小亮的乘车路程为8km。
【拓展提高】1.
如图,公路上有A、B、C三个汽车站,一辆汽车8:00从离A站10km处的P地出发,向C站匀速行驶,15min后离A站30km
(1)设出发x
h后,汽车离A站y
km,写出
y与
x之间的函数表达式
(2)当汽车行驶到离A站250km的B站时,接到通知要在12:00前赶到离B站60km的C站。汽车按原速行驶,能否准时到达?如果能,那么汽车何时到达C站?
A
P
B
C
【拓展提高】2.某技工培训中心有钳工20名、车工30名。现将这50名技工派往A、B两地工作,两地技工的月工资情况如下:
钳工(元/月)
车工(元/月)
A地
1800
1600
B地
1600
1200
(1)若派往A地
x
名钳工,余下的技工全部派往B地,写出这50名技工的月工资总额
y(元)与
x
之间的函数表达式,并写出x的取值范围。
(2)若派往A地
x
名车工,余下的技工全部派往B地,写出这50名技工的月工资总额
y(元)与
x
之间的函数表达式,并写出x的取值范围。
【拓展提高】某技工培训中心有钳工20名、车工30名。现将这50名技工派往A、B两地工作,两地技工的月工资情况如下:
钳工(元/月)
车工(元/月)
A地
1800
1600
B地
1600
1200
(1)若派往A地
x
名钳工,余下的技工全部派往B地,写出这50名技工的月工资总额
y(元)与
x
之间的函数表达式,并写出x的取值范围。
B地
20名钳工
30名车工
A地
x
20-x
30
【拓展提高】某技工培训中心有钳工20名、车工30名。现将这50名技工派往A、B两地工作,两地技工的月工资情况如下:
钳工(元/月)
车工(元/月)
A地
1800
1600
B地
1600
1200
(2)若派往A地
x
名车工,余下的技工全部派往B地,写出这50名技工的月工资总额
y(元)与
x
之间的函数表达式,并写出x的取值范围。
B地
20名钳工
30名车工
A地
30-x
x
20
转化
(一次函数)
解决
实际问题
数学模型
【小结】
通过这节课的学习,你学习到什么新知识?获得了什么经验?还有什么疑问?
【作业】教科书P159习题6.4——1、2、4.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
