3.4.1 第2课时 相似三角形的判定定理1 课件(共15张PPT)
文档属性
| 名称 | 3.4.1 第2课时 相似三角形的判定定理1 课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-10 06:53:14 | ||
图片预览






文档简介
(共15张PPT)
3.4.1相似三角形的判定定理1
湘教版·九年级数学上册
激趣引入
A
B
C
一块三角形玻璃碎了,只留下了完整的∠A和∠B,用这两个角可以去配制一块完全一模一样的玻璃吗?
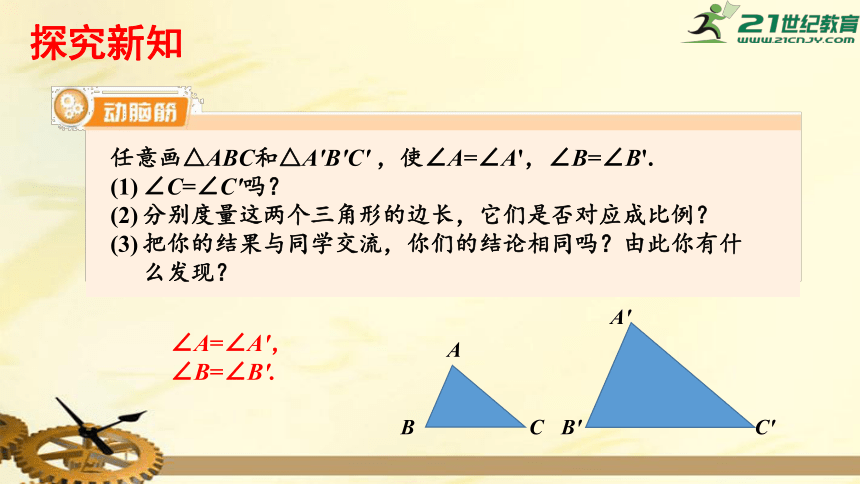
任意画△ABC和△A'B'C'
,使∠A=∠A',∠B=∠B'.
∠C=∠C'吗?
分别度量这两个三角形的边长,它们是否对应成比例?
把你的结果与同学交流,你们的结论相同吗?由此你有什么发现?
A
B
C
A′
B′
C′
探究新知
∠A=∠A',
∠B=∠B'.
A
B
C
A′
B′
C′
在△ABC与△A'B'C'中,已知∠A=∠A',∠B=∠B'.
在△A'B'C'的边A'B'上取一点D,使A'D=AB.
过点D作DE∥B'C',交A′C′于点E.
在△A'DE与△ABC中,
∵∠A′=∠A,A′D=AB,
∠A′DE=∠B′=∠B
,
∴△A'DE≌△ABC.
又
DE∥B'C',
∴△A'DE∽△A'B'C'.
∴△ABC∽△A'B'C'.
两角分别相等的两个三角形相似.
D
E
例3
如图,在△ABC中,∠C=90°.过点D分别作边AB,BC的垂线,垂足分别为点E,F,DF与AB交于点H.求证:△DEH∽△BCA.
证明:∵∠C=90°,∴AC⊥BC.
∵DF⊥BC,∴DF∥AC.
∴∠BHF=∠A,而∠BHF=∠DHE,
∴∠DHE
=∠A.
又DE⊥AB,∴∠DEH=90°=∠C,
∴
△DEH∽△BCA(两角分别相等的两个三角形相似).
如图,在△ABC中,AB=AC,BD=CD,CE⊥AB于E.求证:△ABD∽△CBE.
分析:已知∠B是公共角,判定两三角形相似,再找一组角相等即可,由题易证AD⊥BC,有∠ADB=∠CEB=90°,即可得证.
证明:在△ABC中,AB=AC,BD=CD,
∴AD⊥BC,
∵CE⊥AB,
∴∠ADB=∠CEB=90°,又∠B=∠B,
∴△ABD∽△CBE.
例4
如图,在Rt△ABC与Rt△DEF中,∠C=90°,
∠F=90°.若∠A=∠D,AB=5,BC=4,DE=3,求EF的长.
解:∵∠C=90°,
∠F=90°,∠A=∠D,
∴
△ABC∽△DEF.
∴
又
AB=5,BC=4,DE=3.
∴EF=2.4.
两角分别相等的两个三角形相似
分析:证明相似三角形应先找相等的角,显然∠C是公共角,而另一组相等的角则可以通过计算来求得.借助于计算也是一种常用的方法.
证明:∵∠A=36°,△ABC是等腰三角形,
∴∠ABC=∠C=72°,
又BD平分∠ABC,则∠DBC=36°,
在△ABC和△BCD中,∠C为公共角,∠A=∠DBC=36°,
∴△ABC∽△BCD.
已知△ABC中,AB=AC,∠A=36°,BD是角平分线,求证:△ABC∽△BCD.
已知:如图,在Rt△ABC中,CD是斜边AB
上的高.
求证:△ACD∽△ABC∽△CBD.
证明:
∵∠A=∠A,∠ADC=∠ACB=90°,
∴△ACD∽△ABC,(两角分别相等的两个三角形相似)
同理△CBD∽△ABC,
∴△ABC∽△CBD∽△ACD.
练习
课后练习
1.如图,点E为□ABCD
的边BC延长线上一点,连接AE,交CD于点F.请指出图中有几对相似三角形,并说明理由.
△ABE∽△FCE,
证明:∵四边形ABCD为平行四边形,
∴CD∥AB,AD∥BE.
∴△ABE∽△FCE,∠FCE=∠D,∠E=∠DAF.
∴△FCE∽△FDA.
△FCE∽△FDA,
△ABE∽△FDA
∴△ABE∽△FDA.
2.如图,AB⊥BD,ED⊥BD,点C是线段BD的中点,
且AC⊥CE.已知ED=1,BD=4,求AB的长.
证明:∵
AB⊥BD,ED⊥BD,
AC⊥CE,
∴∠B=∠D=∠ACE=90°.
∵∠A+∠ACB=∠ECD+∠ACB=90°,
∴∠A=∠ECD,
∴△ABC∽△CDE.
∴
∵BD=4,C是BD中点,
∴BC=CD=
∴
即AB=4.
课堂小结
A
B
C
A′
B′
C′
D
E
两角分别相等的两个三角形相似.
∠A=∠A',
∠B=∠B'.
∴△ABC∽△A'B'C'.
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
谢谢观看
THANKS
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
3.4.1相似三角形的判定定理1
湘教版·九年级数学上册
激趣引入
A
B
C
一块三角形玻璃碎了,只留下了完整的∠A和∠B,用这两个角可以去配制一块完全一模一样的玻璃吗?
任意画△ABC和△A'B'C'
,使∠A=∠A',∠B=∠B'.
∠C=∠C'吗?
分别度量这两个三角形的边长,它们是否对应成比例?
把你的结果与同学交流,你们的结论相同吗?由此你有什么发现?
A
B
C
A′
B′
C′
探究新知
∠A=∠A',
∠B=∠B'.
A
B
C
A′
B′
C′
在△ABC与△A'B'C'中,已知∠A=∠A',∠B=∠B'.
在△A'B'C'的边A'B'上取一点D,使A'D=AB.
过点D作DE∥B'C',交A′C′于点E.
在△A'DE与△ABC中,
∵∠A′=∠A,A′D=AB,
∠A′DE=∠B′=∠B
,
∴△A'DE≌△ABC.
又
DE∥B'C',
∴△A'DE∽△A'B'C'.
∴△ABC∽△A'B'C'.
两角分别相等的两个三角形相似.
D
E
例3
如图,在△ABC中,∠C=90°.过点D分别作边AB,BC的垂线,垂足分别为点E,F,DF与AB交于点H.求证:△DEH∽△BCA.
证明:∵∠C=90°,∴AC⊥BC.
∵DF⊥BC,∴DF∥AC.
∴∠BHF=∠A,而∠BHF=∠DHE,
∴∠DHE
=∠A.
又DE⊥AB,∴∠DEH=90°=∠C,
∴
△DEH∽△BCA(两角分别相等的两个三角形相似).
如图,在△ABC中,AB=AC,BD=CD,CE⊥AB于E.求证:△ABD∽△CBE.
分析:已知∠B是公共角,判定两三角形相似,再找一组角相等即可,由题易证AD⊥BC,有∠ADB=∠CEB=90°,即可得证.
证明:在△ABC中,AB=AC,BD=CD,
∴AD⊥BC,
∵CE⊥AB,
∴∠ADB=∠CEB=90°,又∠B=∠B,
∴△ABD∽△CBE.
例4
如图,在Rt△ABC与Rt△DEF中,∠C=90°,
∠F=90°.若∠A=∠D,AB=5,BC=4,DE=3,求EF的长.
解:∵∠C=90°,
∠F=90°,∠A=∠D,
∴
△ABC∽△DEF.
∴
又
AB=5,BC=4,DE=3.
∴EF=2.4.
两角分别相等的两个三角形相似
分析:证明相似三角形应先找相等的角,显然∠C是公共角,而另一组相等的角则可以通过计算来求得.借助于计算也是一种常用的方法.
证明:∵∠A=36°,△ABC是等腰三角形,
∴∠ABC=∠C=72°,
又BD平分∠ABC,则∠DBC=36°,
在△ABC和△BCD中,∠C为公共角,∠A=∠DBC=36°,
∴△ABC∽△BCD.
已知△ABC中,AB=AC,∠A=36°,BD是角平分线,求证:△ABC∽△BCD.
已知:如图,在Rt△ABC中,CD是斜边AB
上的高.
求证:△ACD∽△ABC∽△CBD.
证明:
∵∠A=∠A,∠ADC=∠ACB=90°,
∴△ACD∽△ABC,(两角分别相等的两个三角形相似)
同理△CBD∽△ABC,
∴△ABC∽△CBD∽△ACD.
练习
课后练习
1.如图,点E为□ABCD
的边BC延长线上一点,连接AE,交CD于点F.请指出图中有几对相似三角形,并说明理由.
△ABE∽△FCE,
证明:∵四边形ABCD为平行四边形,
∴CD∥AB,AD∥BE.
∴△ABE∽△FCE,∠FCE=∠D,∠E=∠DAF.
∴△FCE∽△FDA.
△FCE∽△FDA,
△ABE∽△FDA
∴△ABE∽△FDA.
2.如图,AB⊥BD,ED⊥BD,点C是线段BD的中点,
且AC⊥CE.已知ED=1,BD=4,求AB的长.
证明:∵
AB⊥BD,ED⊥BD,
AC⊥CE,
∴∠B=∠D=∠ACE=90°.
∵∠A+∠ACB=∠ECD+∠ACB=90°,
∴∠A=∠ECD,
∴△ABC∽△CDE.
∴
∵BD=4,C是BD中点,
∴BC=CD=
∴
即AB=4.
课堂小结
A
B
C
A′
B′
C′
D
E
两角分别相等的两个三角形相似.
∠A=∠A',
∠B=∠B'.
∴△ABC∽△A'B'C'.
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
谢谢观看
THANKS
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
