3.5 相似三角形的应用 课件(共17张PPT)
文档属性
| 名称 | 3.5 相似三角形的应用 课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-10 07:01:55 | ||
图片预览






文档简介
(共17张PPT)
3.5
相似三角形的应用
湘教版·九年级数学上册
回顾导入
相似三角形有哪些性质?
1.相似三角形对应角相等.
2.相似三角形对应边成比例.
3.相似三角形的周长之比等于相似比.
4.相似三角形的面积之比等于相似比的平方.
5.相似三角形对应边上的高之比、对应边上中线之比、对应角平分线之比等于相似比.
探索新知
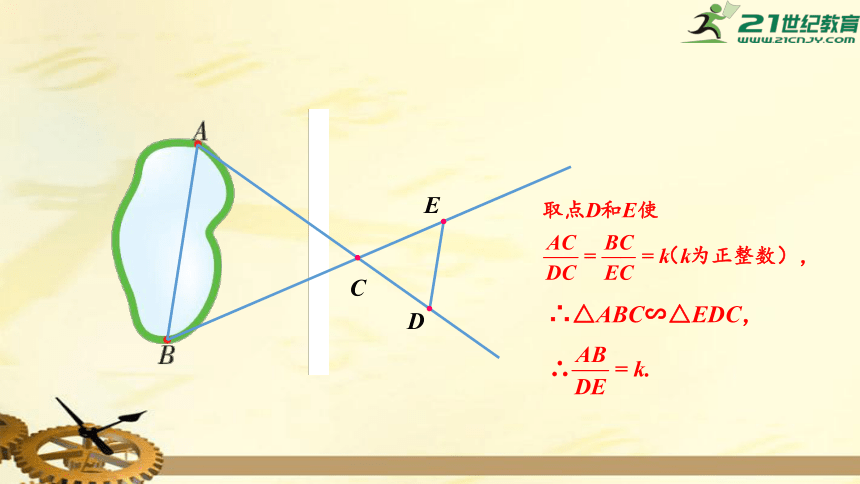
如图,A、B两点分别位于一个池塘的两端,小张想测量出A、B间的距离,但由于受条件限制无法直接测量,你能帮他想出一个可行的测量办法吗?
C
E
D
∴△ABC∽△EDC,
C
DE=50m
∵DE=50m,
∴△ABC∽△EDC.
∴AB=2DE=100m.
E
D
例
在用步枪瞄准靶心时,要使眼睛(O)、准星(A)、
靶心点(B)在同一条直线上.在射击时,李明由于有轻微的抖动,致使准星A偏离到A',如图所示.已知OA=0.2m,OB=50m,
AA'=0.000
5m,求李明射击到的点B'偏离靶心点B的长度BB'(近似地认为AA'//BB').
解:∵AA′∥BB′,
∴△OAA′∽△OBB′.
∵OA=0.2m,OB=50m,AA′=0.0005m,
∴BB′=0.125m.
答:李明射击到的点B′偏离把心点B的长度BB′为0.125m.
练习
课堂练习
1.如图,某路口栏杆的短臂长为1m,长臂长为6m.当短臂端点下降0.5m时,长臂端点升高多少米?
O
A
B
C
D
解:∵AB∥CD,
∴△OAB∽△ODC.
∵OA=1m,AB=0.5m,
OD=6m,
∴CD=3m.
答:长臂端点升高3m.
2.如图,小红同学用自制的直角三角形纸板
DEF测量
树的高度AB,她调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边
DE=80cm,EF=40cm,测得AC=1.5m,CD=8m,求树高AB.
解:∵∠DEF=∠DCB=90°,∠D=∠D,
∴△DEF∽△DCB.
∵DE=80cm,EF=40cm,
CD=8m=800cm,
∴BC=400cm=4m,
答:树高AB为5.5m.
∴AB=4+1.5=5.5m.
3.如图,已知零件的外径为a,要求它的厚度x,需先求
出内孔的直径AB,现用一个交叉卡钳(两条尺长AC和BD相等)
去量,若OA∶OC=OB∶OD=n,且量得CD=b,求厚度x.
分析:如图,要想求厚度x,根据条件可知,首先得求出内孔直径AB.而在图中可构造出相似形,通过相似形的性质,从而求出AB的长度.
解:∵
OA∶OC=OB∶OD=n,且∠AOB=∠COD;
∴△AOB∽△COD.
∴
OA∶OC=AB∶CD=n,
又∵CD=b,
∴AB=CD·n
=nb,
∴x=
4.如图,△ABC是一块锐角三角形材料,边BC=120毫米,
高AD=80毫米,要把它加工成正方形零件,使正方形的一边在
BC在上,其余两个顶点分别在AB、AC上,这个正方形零件的
边长是多少?
解:设正方形PQMN是符合要求的,△ABC的高AD与PN相交于点E.
设正方形PQMN的边长为x毫米.
因为PN∥BC,所以△APN∽
△ABC
所以
因此
答:这个正方形零件的边长是48毫米.
得x=48.
5.如图是步枪在瞄准时的示意图,从眼睛到准星的距离
OE为80cm,步枪上的准星宽度AB为0.2cm,目标的正面宽度CD
为50cm,则眼睛到目标的距离OF是多少?
分析:设眼睛到目标的距离为xcm,由于OE=80cm,AB=0.2cm,CD=50cm,又由于AB∥CD,所以利用相似三角形的性质即可求解.
解:设眼睛到目标的距离为xcm,
∵OE=80cm,AB=0.2cm,CD=50cm,
∵AB∥CD,∴△OBE∽△ODF,
解得x=20000.因为20000cm=200m,
所以眼睛到目标的距离OF是200m.
课堂小结
1.相似三角形对应角相等.
2.相似三角形对应边成比例.
3.相似三角形的周长之比等于相似比.
4.相似三角形的面积之比等于相似比的平方.
5.相似三角形对应边上的高之比、对应边上中线之比、对应角平分线之比等于相似比.
利用相似三角形的性质解决实际问题
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
谢谢观看
THANKS
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
3.5
相似三角形的应用
湘教版·九年级数学上册
回顾导入
相似三角形有哪些性质?
1.相似三角形对应角相等.
2.相似三角形对应边成比例.
3.相似三角形的周长之比等于相似比.
4.相似三角形的面积之比等于相似比的平方.
5.相似三角形对应边上的高之比、对应边上中线之比、对应角平分线之比等于相似比.
探索新知
如图,A、B两点分别位于一个池塘的两端,小张想测量出A、B间的距离,但由于受条件限制无法直接测量,你能帮他想出一个可行的测量办法吗?
C
E
D
∴△ABC∽△EDC,
C
DE=50m
∵DE=50m,
∴△ABC∽△EDC.
∴AB=2DE=100m.
E
D
例
在用步枪瞄准靶心时,要使眼睛(O)、准星(A)、
靶心点(B)在同一条直线上.在射击时,李明由于有轻微的抖动,致使准星A偏离到A',如图所示.已知OA=0.2m,OB=50m,
AA'=0.000
5m,求李明射击到的点B'偏离靶心点B的长度BB'(近似地认为AA'//BB').
解:∵AA′∥BB′,
∴△OAA′∽△OBB′.
∵OA=0.2m,OB=50m,AA′=0.0005m,
∴BB′=0.125m.
答:李明射击到的点B′偏离把心点B的长度BB′为0.125m.
练习
课堂练习
1.如图,某路口栏杆的短臂长为1m,长臂长为6m.当短臂端点下降0.5m时,长臂端点升高多少米?
O
A
B
C
D
解:∵AB∥CD,
∴△OAB∽△ODC.
∵OA=1m,AB=0.5m,
OD=6m,
∴CD=3m.
答:长臂端点升高3m.
2.如图,小红同学用自制的直角三角形纸板
DEF测量
树的高度AB,她调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边
DE=80cm,EF=40cm,测得AC=1.5m,CD=8m,求树高AB.
解:∵∠DEF=∠DCB=90°,∠D=∠D,
∴△DEF∽△DCB.
∵DE=80cm,EF=40cm,
CD=8m=800cm,
∴BC=400cm=4m,
答:树高AB为5.5m.
∴AB=4+1.5=5.5m.
3.如图,已知零件的外径为a,要求它的厚度x,需先求
出内孔的直径AB,现用一个交叉卡钳(两条尺长AC和BD相等)
去量,若OA∶OC=OB∶OD=n,且量得CD=b,求厚度x.
分析:如图,要想求厚度x,根据条件可知,首先得求出内孔直径AB.而在图中可构造出相似形,通过相似形的性质,从而求出AB的长度.
解:∵
OA∶OC=OB∶OD=n,且∠AOB=∠COD;
∴△AOB∽△COD.
∴
OA∶OC=AB∶CD=n,
又∵CD=b,
∴AB=CD·n
=nb,
∴x=
4.如图,△ABC是一块锐角三角形材料,边BC=120毫米,
高AD=80毫米,要把它加工成正方形零件,使正方形的一边在
BC在上,其余两个顶点分别在AB、AC上,这个正方形零件的
边长是多少?
解:设正方形PQMN是符合要求的,△ABC的高AD与PN相交于点E.
设正方形PQMN的边长为x毫米.
因为PN∥BC,所以△APN∽
△ABC
所以
因此
答:这个正方形零件的边长是48毫米.
得x=48.
5.如图是步枪在瞄准时的示意图,从眼睛到准星的距离
OE为80cm,步枪上的准星宽度AB为0.2cm,目标的正面宽度CD
为50cm,则眼睛到目标的距离OF是多少?
分析:设眼睛到目标的距离为xcm,由于OE=80cm,AB=0.2cm,CD=50cm,又由于AB∥CD,所以利用相似三角形的性质即可求解.
解:设眼睛到目标的距离为xcm,
∵OE=80cm,AB=0.2cm,CD=50cm,
∵AB∥CD,∴△OBE∽△ODF,
解得x=20000.因为20000cm=200m,
所以眼睛到目标的距离OF是200m.
课堂小结
1.相似三角形对应角相等.
2.相似三角形对应边成比例.
3.相似三角形的周长之比等于相似比.
4.相似三角形的面积之比等于相似比的平方.
5.相似三角形对应边上的高之比、对应边上中线之比、对应角平分线之比等于相似比.
利用相似三角形的性质解决实际问题
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
谢谢观看
THANKS
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
