第三章 图形的相似 章末复习课件(共34张PPT)
文档属性
| 名称 | 第三章 图形的相似 章末复习课件(共34张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-10 07:07:42 | ||
图片预览










文档简介
(共34张PPT)
第三章
章末复习
湘教版·九年级数学上册
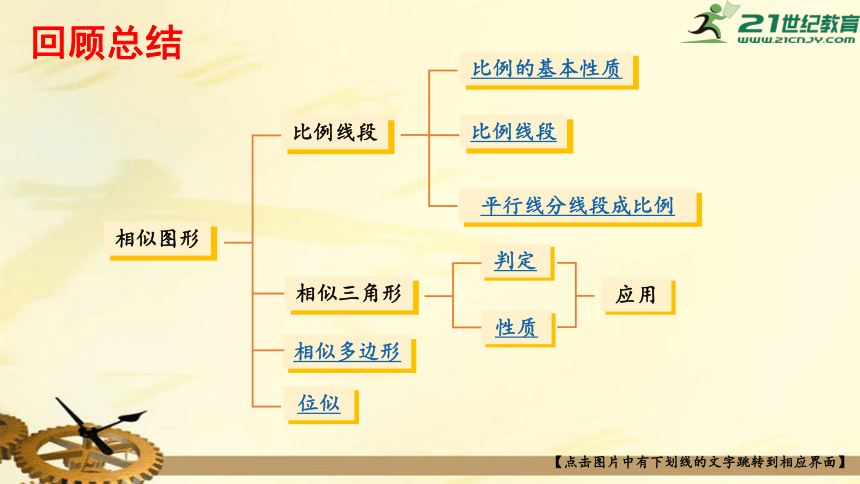
回顾总结
相似图形
比例线段
相似三角形
相似多边形
位似
比例的基本性质
比例线段
平行线分线段成比例
判定
性质
应用
【点击图片中有下划线的文字跳转到相应界面】
比例的基本性质:
如果ad=bc,其中a,b,c,d为非零实数,那么
成立.
首页
已知四条线段a,b,c,d中,若
,则a,b,c,d是比例线段.
类似地,如果
,那么称线段AB,BC,AC与线段A′B′
,B′C′
,A′C′对应成比例.
黄金分割比为
,它约等于0.618.
比例线段
首页
两条直线被一组平行线所截,如果在其中一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等.
平行线分线段成比例
两条直线被一组平行线所截,所得的对应线段成正比例.
平行于三角形一边的直线截其他两边,所得的对应线段成比例.
平行线分线段成比例
首页
两角分别相等的两个三角形相似.
相似三角形判定定理1
两边成比例且夹角相等的两个三角形相似.
相似三角形判定定理2
三边成比例的两个三角形相似.
相似三角形判定定理3
首页
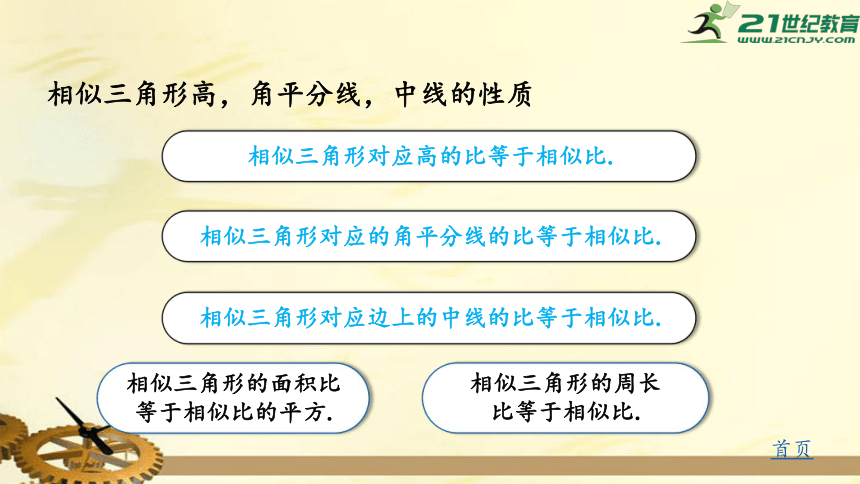
相似三角形高,角平分线,中线的性质
相似三角形对应高的比等于相似比.
相似三角形对应边上的中线的比等于相似比.
相似三角形对应的角平分线的比等于相似比.
相似三角形的面积比等于相似比的平方.
相似三角形的周长比等于相似比.
首页
对于两个边数相同的多边形,如果他们的对应角相等,对应边成比例,那么这两个多边形叫作相似多边形.相似多边形的对应边的比也叫作相似比.
相似多边形
首页
位似
首页
一般地,取定一个点O,如果一个图形G上每一个点P对应
于另一个图形G′上的点P′,且满足:
那么称图形G与图形G′是位似图形.这个点O叫作位似中心,常数k叫作位似比.
(1)直线PP′经过点O,
(2)
,其中k是非零常数,当k>0时,点P′在射线OP上,当k<0时,点P′在射线OP的反向延长线上.
课堂练习
A
组
∵DE=6,
∴EF=4.
∴DF=DE+EF=4+6=10.
解:∵l1∥l2∥l3,
解:∵∠C=∠D=90°,
∠CAB=∠DAE,
∴△ACB∽△ADE.
∵CB=9.8m,AC=14.2m,AD=28.4m,
∴ED=19.6m.
证明:∵AC=5,BC=3,EC=10,DC=6,
∴△ACB∽△ECD,
∴AB∥DE.
又∠ACB=∠ECD,
∴∠A=∠E,
∵AB=14km,AD=28km,BD=21km,BC=42km,DC=31.5km
∴△ABD∽△BDC,
∴AB∥DC.
∴∠ABD=∠BDC,
解:平行,理由如下:
相似三角形对应边上的中线的比等于相似比.
相似三角形的面积比等于相似比的平方.
相似三角形的周长比等于相似比.
∴△DEF面积为56.25
∴△DEF周长为24
解:∵∠1=∠2,
∴∠CED=∠AEB,
又∠CDE=∠ABE=90°,
∴△CED∽△AEB,
∵DE=3m,CD=1.5m,BE=8m,
∴AB=4m.
答:树AB的高度为4m.
∴BE=55.2m
答:此时他与教学楼的距离BE为55.2m.
M
解:过点F作FM⊥DC于M,交AB于点N.易得△AFN∽△DFM,
N
A′
B′
C′
D′
A′′
B′′
C′′
D′′
是位似图形.
A′
B′
C′
D′
A′′
B′′
C′′
D′′
是位似图形.
B
组
证明
:(1)∵CD是斜边AB上的高,∴∠ADC=90°,在△ACB和△ADC中,
∴△ACB∽△ADC,
在△ACB和△ADC中,∵∠ACB=∠ADC=90°,∠A=∠A,
(2)在Rt△ABC中,∵∠ACB=90°,∴∠A+∠B=90°,
∵CD⊥AB,
∴
△BDC∽△CDA,
∴∠B+∠BCD=90°,
∴∠A=∠BCD,又∠BDC=∠CDA,
解:∵AE∥DB,∴△BCD∽△ACE,
∵DE=2.7m,CE=8.7m,AB=1.8m,
∴BC=4m.
答:窗口底边离地面的高是4m.
当△ABE∽△NDM,
解:由题意可得,BE=1,AE=
.当△ABE∽△MDN,
解:四边形A′B′C′D′与四边形ABCD相似,理由如下:
且AA′,
BB′,
CC′,
DD′,都经过同一个点O,
∴四边形A′B′C′D′与四边形ABCD是位似图形,
故可得四边形A′B′C′D′∽四边形ABCD.
(-2,4)
(-4,0)
(2,4)
(4,-2)
(2,-6)
(-2,-4)
C
组
解:能,过点P作PH⊥AB交直线AB于点H,则有PH∥EF,PH∥CD.
设PH=hm,FH=xm.
在△BFE和△BHP中,
∵∠BFE=∠BHP=90°,
∠EBF=∠PBH,
∴△BFE∽△BHP,
同理可得△ADC∽△AHP,
∴
h=2(0.6+x).
①
∴0.8h=3.1+x.
②
h≈8.3.
联立①②可得
H
答:支架顶端Р到地面的距离约为8.3m.
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
谢谢观看
THANKS
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
第三章
章末复习
湘教版·九年级数学上册
回顾总结
相似图形
比例线段
相似三角形
相似多边形
位似
比例的基本性质
比例线段
平行线分线段成比例
判定
性质
应用
【点击图片中有下划线的文字跳转到相应界面】
比例的基本性质:
如果ad=bc,其中a,b,c,d为非零实数,那么
成立.
首页
已知四条线段a,b,c,d中,若
,则a,b,c,d是比例线段.
类似地,如果
,那么称线段AB,BC,AC与线段A′B′
,B′C′
,A′C′对应成比例.
黄金分割比为
,它约等于0.618.
比例线段
首页
两条直线被一组平行线所截,如果在其中一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等.
平行线分线段成比例
两条直线被一组平行线所截,所得的对应线段成正比例.
平行于三角形一边的直线截其他两边,所得的对应线段成比例.
平行线分线段成比例
首页
两角分别相等的两个三角形相似.
相似三角形判定定理1
两边成比例且夹角相等的两个三角形相似.
相似三角形判定定理2
三边成比例的两个三角形相似.
相似三角形判定定理3
首页
相似三角形高,角平分线,中线的性质
相似三角形对应高的比等于相似比.
相似三角形对应边上的中线的比等于相似比.
相似三角形对应的角平分线的比等于相似比.
相似三角形的面积比等于相似比的平方.
相似三角形的周长比等于相似比.
首页
对于两个边数相同的多边形,如果他们的对应角相等,对应边成比例,那么这两个多边形叫作相似多边形.相似多边形的对应边的比也叫作相似比.
相似多边形
首页
位似
首页
一般地,取定一个点O,如果一个图形G上每一个点P对应
于另一个图形G′上的点P′,且满足:
那么称图形G与图形G′是位似图形.这个点O叫作位似中心,常数k叫作位似比.
(1)直线PP′经过点O,
(2)
,其中k是非零常数,当k>0时,点P′在射线OP上,当k<0时,点P′在射线OP的反向延长线上.
课堂练习
A
组
∵DE=6,
∴EF=4.
∴DF=DE+EF=4+6=10.
解:∵l1∥l2∥l3,
解:∵∠C=∠D=90°,
∠CAB=∠DAE,
∴△ACB∽△ADE.
∵CB=9.8m,AC=14.2m,AD=28.4m,
∴ED=19.6m.
证明:∵AC=5,BC=3,EC=10,DC=6,
∴△ACB∽△ECD,
∴AB∥DE.
又∠ACB=∠ECD,
∴∠A=∠E,
∵AB=14km,AD=28km,BD=21km,BC=42km,DC=31.5km
∴△ABD∽△BDC,
∴AB∥DC.
∴∠ABD=∠BDC,
解:平行,理由如下:
相似三角形对应边上的中线的比等于相似比.
相似三角形的面积比等于相似比的平方.
相似三角形的周长比等于相似比.
∴△DEF面积为56.25
∴△DEF周长为24
解:∵∠1=∠2,
∴∠CED=∠AEB,
又∠CDE=∠ABE=90°,
∴△CED∽△AEB,
∵DE=3m,CD=1.5m,BE=8m,
∴AB=4m.
答:树AB的高度为4m.
∴BE=55.2m
答:此时他与教学楼的距离BE为55.2m.
M
解:过点F作FM⊥DC于M,交AB于点N.易得△AFN∽△DFM,
N
A′
B′
C′
D′
A′′
B′′
C′′
D′′
是位似图形.
A′
B′
C′
D′
A′′
B′′
C′′
D′′
是位似图形.
B
组
证明
:(1)∵CD是斜边AB上的高,∴∠ADC=90°,在△ACB和△ADC中,
∴△ACB∽△ADC,
在△ACB和△ADC中,∵∠ACB=∠ADC=90°,∠A=∠A,
(2)在Rt△ABC中,∵∠ACB=90°,∴∠A+∠B=90°,
∵CD⊥AB,
∴
△BDC∽△CDA,
∴∠B+∠BCD=90°,
∴∠A=∠BCD,又∠BDC=∠CDA,
解:∵AE∥DB,∴△BCD∽△ACE,
∵DE=2.7m,CE=8.7m,AB=1.8m,
∴BC=4m.
答:窗口底边离地面的高是4m.
当△ABE∽△NDM,
解:由题意可得,BE=1,AE=
.当△ABE∽△MDN,
解:四边形A′B′C′D′与四边形ABCD相似,理由如下:
且AA′,
BB′,
CC′,
DD′,都经过同一个点O,
∴四边形A′B′C′D′与四边形ABCD是位似图形,
故可得四边形A′B′C′D′∽四边形ABCD.
(-2,4)
(-4,0)
(2,4)
(4,-2)
(2,-6)
(-2,-4)
C
组
解:能,过点P作PH⊥AB交直线AB于点H,则有PH∥EF,PH∥CD.
设PH=hm,FH=xm.
在△BFE和△BHP中,
∵∠BFE=∠BHP=90°,
∠EBF=∠PBH,
∴△BFE∽△BHP,
同理可得△ADC∽△AHP,
∴
h=2(0.6+x).
①
∴0.8h=3.1+x.
②
h≈8.3.
联立①②可得
H
答:支架顶端Р到地面的距离约为8.3m.
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
谢谢观看
THANKS
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
