2021-2022学年湘教新版九年级上册数学《第1章 反比例函数》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年湘教新版九年级上册数学《第1章 反比例函数》单元测试卷(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 509.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-08 17:51:17 | ||
图片预览




文档简介
2021-2022学年湘教新版九年级上册数学《第1章
反比例函数》单元测试卷
一.选择题
1.下面四个关系式中,y是x的反比例函数的是( )
A.y=
B.yx=﹣
C.y=5x+6
D.=
2.如图,以原点为圆心的圆与反比例函数y=的图象交于A、B、C、D四点,已知点A的横坐标为1,则点C的横坐标( )
A.﹣4
B.﹣3
C.﹣2
D.﹣1
3.对于反比例函数y=,下列判断正确的是( )
A.图象经过点(﹣1,3)
B.图象在第二、四象限
C.不论x为何值,y>0
D.图象所在的第一象限内,y随x的增大而减小
4.当x=2时,正比例函数y=k1x(k1≠0)与反比例函数y=(k2≠0)的值相等,则k1与k2的比是( )
A.4:1
B.2:1
C.1:2
D.1:4
5.矩形面积是40m2,设它的一边长为x(m),则矩形的另一边长y(m)与x的函数关系是( )
A.y=20﹣x
B.y=40x
C.y=
D.y=
6.已知m<0,则函数y=的图象大致是( )
A.
B.
C.
D.
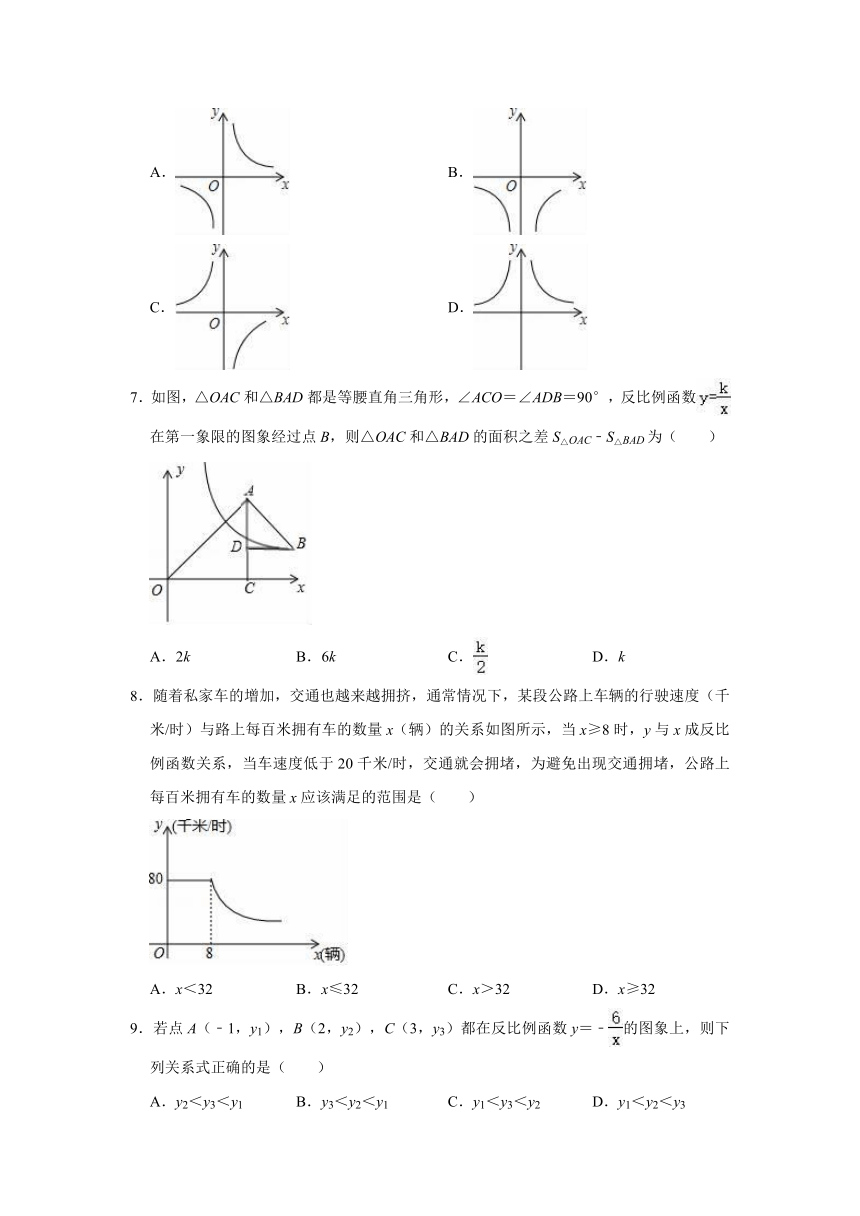
7.如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数在第一象限的图象经过点B,则△OAC和△BAD的面积之差S△OAC﹣S△BAD为( )
A.2k
B.6k
C.
D.k
8.随着私家车的增加,交通也越来越拥挤,通常情况下,某段公路上车辆的行驶速度(千米/时)与路上每百米拥有车的数量x(辆)的关系如图所示,当x≥8时,y与x成反比例函数关系,当车速度低于20千米/时,交通就会拥堵,为避免出现交通拥堵,公路上每百米拥有车的数量x应该满足的范围是( )
A.x<32
B.x≤32
C.x>32
D.x≥32
9.若点A(﹣1,y1),B(2,y2),C(3,y3)都在反比例函数y=﹣的图象上,则下列关系式正确的是( )
A.y2<y3<y1
B.y3<y2<y1
C.y1<y3<y2
D.y1<y2<y3
10.若函数的图象经过点(3,﹣4),则它的图象一定还经过点( )
A.(3,4)
B.(2,6)
C.(﹣12,1)
D.(﹣3,﹣4)
二.填空题
11.如果函数y=x2m﹣1为反比例函数,则m的值是
.
12.已知反比例函数y=(k≠0)的图象与正比例函数y=mx(m≠0)的图象交于点(2,1),则其另一个交点坐标为
.
13.由于天气炎热,某校根据《学校卫生工作条例》,为预防“蚊虫叮咬”,对教室进行“薰药消毒”.已知药物在燃烧机释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所示(即图中线段OA和双曲线在A点及其右侧的部分),当空气中每立方米的含药量低于2毫克时,对人体无毒害作用,那么从消毒开始,至少在
分钟内,师生不能待在教室.
14.已知点(﹣1,y1)、(2,y2)、(,y3)在反比例函数y=﹣的图象上,则y1、y2、y3的大小关系是
.
15.反比例函数y=的图象经过点(﹣3,2),则k的值为
.
16.一批零件300个,一个工人每小时做15个,用关系式表示人数x与完成任务所需的时间y之间的函数关系式为
.
17.如图,平面直角坐标系中,A(8,0),B(8,4),C(0,4),反比例函数y=在第一象限内的图象分别与线段AB、BC交于点F、E,连接EF.如果点B关于EF的对称点恰好落在OA边上.那么k的值为
.
18.如图,在同一平面直角坐标系中,函数y1=kx+b(k、b是常数,且k≠0)与反比例函数y2=(c是常数,且c≠0)的图象相交于A(﹣3,﹣2),B(2,3)两点,则不等式y1>y2的解集是
.
19.如图,在平面直角坐标系中,菱形ABCD的顶点A、B在反比例函数y=(k>0,x>0)的图象上,横坐标分别为1,4,对角线BD∥x轴.若菱形ABCD的面积为,则k的值为
.
20.如图,点A为函数y=(x>0)图象上一点,连接OA,交函数y=(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为
.
三.解答题
21.已知关于x的反比例函数.
(1)求m的值;
(2)它的图象位于哪些象限?
22.有这样一个问题:探究函数y=的图象与性质.小彤根据学习函数的经验,对函数y=的图象与性质进行了探究.
下面是小彤探究的过程,请补充完整:
(1)函数y=的自变量x的取值范围是
;
(2)下表是y与x的几组对应值:
x
…
﹣2
﹣1
0
1
2
4
5
6
7
8
…
y
…
m
0
﹣1
3
2
…
则m的值为
;
(3)如图所示,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出了图象的一部分,请根据剩余的点补全此函数的图象;
(4)观察图象,写出该函数的一条性质
;
(5)若函数y=的图象上有三个点A(x1,y1)、B(x2,y2)、C(x3,y3),且x1<3<x2<x3,则y1、y2、y3之间的大小关系为
;
23.小楠是一个乐学习,善思考,爱探究的同学,她对函数的图象和性质进行了探究,请你将下列探究过程补充完整:
(Ⅰ)函数的自变量x的取值范围是
.
(Ⅱ)用描点法画函数图象:
(i)列表:
x
…
﹣5
﹣2
﹣1
0
…
2
3
4
7
…
y
…
a
2
3
b
…
6
3
2
1
…
表中a的值为
,b的值为
.
(ii)描点连线:请在右图画出该图象的另一部分.
(Ⅲ)观察函数图象,得到函数的性质:
当x
时,函数值y随x的增大而
;
当x
时,函数值y随x的增大而减少.
(IV)应用:若≥6,则x的取值范围是
.
24.如图,已知∠AOB=90°,∠OAB=30°,反比例函数y=﹣(x<0)的图象过点B(﹣3,a),反比例函数y=(x>0)的图象过点A.
(1)求a和k的值;
(2)过点B作BC∥x轴,与双曲线y=交于点C.求△OAC的面积.
25.点A是反比例函数y=(x>0)的图象l1上一点,直线AB∥x轴,交反比例函数y=(x>0)的图象l2于点B,直线AC∥y轴,交l2于点C,直线CD∥x轴,交l1于点D.
(1)若点A(1,1),求线段AB和CD的长度;
(2)对于任意的点A(a,b),判断线段AB和CD的大小关系,并证明.
26.如图1,点A(m,6),B(6,1)在反比例函数图象上,作直线AB,连接OA、OB.
(1)求反比例函数的表达式和m的值;
(2)求△AOB的面积;
(3)如图2,E是线段AB上一点,作AD⊥x轴于点D,过点E作x轴的垂线,交反比例函数图象于点F,若EF=AD,求出点E的坐标.
27.在平面直角坐标系xOy中,已知直线y=x与双曲线y=的一个交点是A(2,a).
(1)求k的值;
(2)设点P(m,n)是双曲线y=上不同于A的一点,直线PA与x轴交于点B(b,0).
①若m=1,求b的值;
②若PB=2AB,结合图象,直接写出b的值.
参考答案与试题解析
一.选择题
1.解:A、y=,是y与x2成反比例函数关系,故此选项错误;
B、yx=﹣,y是x的反比例函数,故此选项正确;
C、y=5x+6是一次函数关系,故此选项错误;
D、=,不符合反比例函数关系,故此选项错误.
故选:B.
2.解:把x=1代入y=,得y=3,故A点坐标为(1,3);
∵A、B关于y=x对称,则B点坐标为(3,1);
又∵B和C关于原点对称,
∴C点坐标为(﹣3,﹣1),
∴点C的横坐标为﹣3.
故选:B.
3.解:A、图象经过点(﹣1,3),说法错误;
B、图象在第二、四象限,说法错误;
C、不论x为何值,y>0,说法错误;
D、图象所在的第一象限内,y随x的增大而减小,说法正确;
故选:D.
4.解:∵当x=2时,k1x═,
∴2k1=.
∴=
故选:D.
5.解:由于矩形的另一边长=矩形面积÷一边长,
∴矩形的另一边长y(m)与x的函数关系是y=.
故选:C.
6.解:当x>0时,y==,
∵m<0,
∴图象在第四象限;
当x<0时,y==﹣,
∵m<0,
∴﹣m>0,
∴图象在第三象限;
故选:B.
7.解:设△OAC和△BAD的直角边长分别为a、b,
则点B的坐标为(a+b,a﹣b).
∵点B在反比例函数的第一象限图象上,
∴(a+b)×(a﹣b)=a2﹣b2=k.
∴S△OAC﹣S△BAD=a2﹣b2=(a2﹣b2)=.
故选:C.
8.解:设反比例函数的解析式为:y=(x≥8),
则将(8,80),代入得:y=,
故当车速度为20千米/时,则20=,
解得:x=32,
故高架桥上每百米拥有车的数量x应该满足的范围是:x≤32.
故选:B.
9.解:将点A(﹣1,y1),B(2,y2),C(3,y3)分别代入y=﹣得,
y1=5,y2=﹣3,y3=﹣2,
故y2<y3<y1.
故选:A.
10.解:∵函数的图象经过点(3,﹣4),
∴k=3×(﹣4)=﹣12,
符合题意的只有C:k=﹣12×1=﹣12.
故选:C.
二.填空题
11.解:∵y=x2m﹣1是反比例函数,
∴2m﹣1=﹣1,
解之得:m=0.
故答案为0.
12.解:∵正比例函数与反比例函数的图象均关于原点对称,
∴两函数的交点关于原点对称,
∵一个交点的坐标是(2,1),
∴另一个交点的坐标是(﹣2,﹣1).
故答案为:(﹣2,﹣1).
13.解:设反比例函数解析式为y=(k≠0),
将(25,6)代入解析式得,k=25×6=150,
则函数解析式为y=(x≥15),
当y=2时,=2,
解得x=75.
答:从消毒开始,师生至少在75分钟内不能进入教室.
14.解:∵反比例函数y=﹣中,k=﹣(k2+1)<0,
∴此函数的图象在二、四象限,在每一象限内y随x的增大而增大,
∵﹣1<0<2<,
∴y1>0>y3>y2,
故答案为y1>y3>y2.
15.解:由题意知,k=﹣3×2=﹣6.
故答案为:﹣6.
16.解:由题意得:人数x与完成任务所需的时间y之间的函数关系式为y=300÷15x=.
故本题答案为:y=.
17.解:过点E作EG⊥OA,垂足为G,设点B关于EF的对称点为D,连接ED、DF,如图所示:
则△BEF≌△DEF,
∴BF=DF,BE=DE,∠FDE=∠FBE=90°,
∴∠EDG+∠ADF=∠ADF+∠AFD,
∴∠EDG=∠AFD,
∵∠EGD=∠DAF,
∴△ADF∽△GED,
∴=,
∴AD:EG=BF:BE,
∵A(8,0),B(8,4),C(0,4),
∴AB=OC=EG=4,OA=BC=8,
∵E、F在反比例函数y=的图象上,
∴E(,4)、F(8,)
∴OG=EC=,AF=,
∴BF=4﹣,BE=8﹣,
∴====,
∴AD=EG=2,
在Rt△ADF中,由勾股定理:AD2+AF2=DF2
即:22+()2=(4﹣)2
解得:k=12,
故答案为12.
18.解:∵函数y1=kx+b(k、b是常数,且k≠0)与反比例函数y2=(c是常数,且c≠0)的图象相交于A(﹣3,﹣2),B(2,3)两点
∴以﹣3和2为大小的分界点,﹣3<x<0,x>2是y1函数图象都在y2函数图象的上方,
∴y1>y2
故答案为:﹣3<x<0,x>2.
19.解:连接AC分别交BD、x轴于点E、F.
由已知,A、B横坐标分别为1,4,
∴BE=3,
∵四边形ABCD为菱形,AC、BD为对角线
∴S菱形ABCD=4×AE?BE=,
∴AE=,设点B的坐标为(4,y),则A点坐标为(1,y+)
∵点A、B同在y=图象上
∴4y=1?(y+)
∴y=,
∴B点坐标为(4,)
∴k=5
故答案为5.
20.解:设点A的坐标为(a,),点B的坐标为(b,),
∵点C是x轴上一点,且AO=AC,
∴点C的坐标是(2a,0),
设过点O(0,0),A(a,)的直线的解析式为:y=kx,
∴,
解得,k=,
又∵点B(b,)在y=上,
∴,解得,或(舍去),
∴S△ABC=S△AOC﹣S△OBC==,
故答案为:6.
三.解答题
21.解:(1)∵是关于x的反比例函数,
∴m2﹣5=﹣1,且m﹣2≠0,
∴m的值是﹣2;
(2)当m=﹣2时,m﹣2=﹣2﹣2=﹣4<0,
∴这个反比例函数的图像位于第二、四象限.
22.解:(1)∵x﹣3≠0,
∴x≠3;
(2)当x=﹣1时,y===;
(3)如图所示:
(4)由图象可得,当x>3时,y随x的增大而减小(答案不唯一);
(5)由图象可得,当x1<3时,y1<1;当3<x2<x3时,1<y3<y2.
∴y1、y2、y3之间的大小关系为y1<y3<y2.
故答案为:x≠3;;当x>3时,y随x的增大而减小;y1<y3<y2.
23.解:(Ⅰ)x﹣1≠0,解得x≠1,
故答案为x≠1;
(Ⅱ)(i)当x=﹣5时,a=y==1,b=y==6,
故答案为1,6;
(ii)描点后画出如下函数图象:
(Ⅲ)观察函数图象,得到函数的性质:
当x<1时,函数值y随x的增大而增大;
当x>1时,函数值y随x的增大而减少.
故答案为<1,增大;>1;
(Ⅳ)由图象可知,≥6时x的取值范围是0≤x<1或1<x≤2,
故答案为0≤x<1或1<x≤2.
24.解:(1)∵比例函数y=﹣(x<0)的图象过点B(﹣3,a),
∴a=﹣=1,
∴OE=3,BE=1,
分别过点A、B作AD⊥x轴于D,BE⊥x轴于E,
∴∠BOE+∠OBE=90°,
∵∠AOB=90°,∠OAB=30°,
∴∠BOE+∠AOD=90°,tan30°==,
∴∠OBE=∠AOD,
∵∠OEB=∠ADO=90°,
∴△BOE∽△OAD
∴===,
∴AD=?OE==3,OD=?BE==
∴A(,3),
∵反比例函数y=(x>0)的图象过点A,
∴k=×=9;
(2)由(1)可知
AD=3,OD=,
∵BC∥x轴,B(﹣3,1),
∴C点的纵坐标为1,
过点C作CF⊥x轴于F,
∵点C在双曲线y=上,
∴1=,解得x=9,
∴C(9,1),
∴CF=1,
∴S△AOC=S△AOD+S梯形ADFC﹣S△COF=S梯形ADCF
=(AD+CF)(OF﹣OD)
=(3+1)(9﹣)
=13.
25.解:(1)∵AB∥x轴,A(1,1),B在反比例函数的图象上,
∴B(3,1).
同理可求:C(1,3),D(,3).
∴AB=2,CD=.
(2)AB>CD.
证明:∵A(a,b),A在反比例函数的图象上,
∴A(a,).
∵AB∥x轴,B在反比例函数的图象上,
∴B(3a,).
同理可求:C(a,),D(,).
∴AB=2a,CD=.
∵a>0,
∴2a>.
∴AB>CD.
26.解:(1)设反比例函数的解析式为y=,
将B(6,1)的坐标代入y=,得k=6.
∴反比例函数的解析式为y=.
将A(m,6)的坐标代入y=,得m=1.
(2)如图1,设直线AB的解析式为y=ax+b,
把A(1,6)和B(6,1)代入上式,得
,
解得:,
故直线AB的解析式为:y=﹣x+7,
∴M(0,7),N(7,0),
∴S△AOB=S△MON﹣S△AOM﹣S△BON=OM×ON﹣OM×|xA|﹣ON×|yB|
=×7×7﹣×7×1﹣×7×1
=.
(3)设E点的坐标为(m,﹣m+7),则F(m,),
∴EF=﹣m+7﹣.
∵EF=AD,
∴﹣m+7﹣=×6.
解得m1=2,m2=3,
经检验,m1=2,m2=3是分式方程的根,
∴E的坐标为(2,5)或(3,4).
27.解:(1)∵直线y=x与双曲线y=的一个交点是A(2,a),
∴a=×2=1,
∴A(2,1),
∴k=2×1=2;
(2)①若m=1,则P(1,n),
∵点P(1,n)是双曲线y=上不同于A的一点,
∴n=k=2,
∴P(1,2),
∵A(2,1),
则直线PA的解析式为y=﹣x+3,
∵直线PA与x轴交于点B(b,0),
∴0=﹣b+3,
∴b=3;
②如图1,当P在第一象限时,
∵PB=2AB,A(2,1),
∴P点的纵坐标时2,
代入y=求得x=1,
∴P(1,2),
由①可知,此时b=3;
如图2,当P在第,三象限时,
∵PB=2AB,A(2,1),
∴P点的纵坐标时﹣2,
代入y=求得x=﹣1,
∴P(﹣1,﹣2),
∵A(2,1)
则直线PA的解析式为y=x﹣1,
∴b=1,
综上,b的值为3或1.
反比例函数》单元测试卷
一.选择题
1.下面四个关系式中,y是x的反比例函数的是( )
A.y=
B.yx=﹣
C.y=5x+6
D.=
2.如图,以原点为圆心的圆与反比例函数y=的图象交于A、B、C、D四点,已知点A的横坐标为1,则点C的横坐标( )
A.﹣4
B.﹣3
C.﹣2
D.﹣1
3.对于反比例函数y=,下列判断正确的是( )
A.图象经过点(﹣1,3)
B.图象在第二、四象限
C.不论x为何值,y>0
D.图象所在的第一象限内,y随x的增大而减小
4.当x=2时,正比例函数y=k1x(k1≠0)与反比例函数y=(k2≠0)的值相等,则k1与k2的比是( )
A.4:1
B.2:1
C.1:2
D.1:4
5.矩形面积是40m2,设它的一边长为x(m),则矩形的另一边长y(m)与x的函数关系是( )
A.y=20﹣x
B.y=40x
C.y=
D.y=
6.已知m<0,则函数y=的图象大致是( )
A.
B.
C.
D.
7.如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数在第一象限的图象经过点B,则△OAC和△BAD的面积之差S△OAC﹣S△BAD为( )
A.2k
B.6k
C.
D.k
8.随着私家车的增加,交通也越来越拥挤,通常情况下,某段公路上车辆的行驶速度(千米/时)与路上每百米拥有车的数量x(辆)的关系如图所示,当x≥8时,y与x成反比例函数关系,当车速度低于20千米/时,交通就会拥堵,为避免出现交通拥堵,公路上每百米拥有车的数量x应该满足的范围是( )
A.x<32
B.x≤32
C.x>32
D.x≥32
9.若点A(﹣1,y1),B(2,y2),C(3,y3)都在反比例函数y=﹣的图象上,则下列关系式正确的是( )
A.y2<y3<y1
B.y3<y2<y1
C.y1<y3<y2
D.y1<y2<y3
10.若函数的图象经过点(3,﹣4),则它的图象一定还经过点( )
A.(3,4)
B.(2,6)
C.(﹣12,1)
D.(﹣3,﹣4)
二.填空题
11.如果函数y=x2m﹣1为反比例函数,则m的值是
.
12.已知反比例函数y=(k≠0)的图象与正比例函数y=mx(m≠0)的图象交于点(2,1),则其另一个交点坐标为
.
13.由于天气炎热,某校根据《学校卫生工作条例》,为预防“蚊虫叮咬”,对教室进行“薰药消毒”.已知药物在燃烧机释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所示(即图中线段OA和双曲线在A点及其右侧的部分),当空气中每立方米的含药量低于2毫克时,对人体无毒害作用,那么从消毒开始,至少在
分钟内,师生不能待在教室.
14.已知点(﹣1,y1)、(2,y2)、(,y3)在反比例函数y=﹣的图象上,则y1、y2、y3的大小关系是
.
15.反比例函数y=的图象经过点(﹣3,2),则k的值为
.
16.一批零件300个,一个工人每小时做15个,用关系式表示人数x与完成任务所需的时间y之间的函数关系式为
.
17.如图,平面直角坐标系中,A(8,0),B(8,4),C(0,4),反比例函数y=在第一象限内的图象分别与线段AB、BC交于点F、E,连接EF.如果点B关于EF的对称点恰好落在OA边上.那么k的值为
.
18.如图,在同一平面直角坐标系中,函数y1=kx+b(k、b是常数,且k≠0)与反比例函数y2=(c是常数,且c≠0)的图象相交于A(﹣3,﹣2),B(2,3)两点,则不等式y1>y2的解集是
.
19.如图,在平面直角坐标系中,菱形ABCD的顶点A、B在反比例函数y=(k>0,x>0)的图象上,横坐标分别为1,4,对角线BD∥x轴.若菱形ABCD的面积为,则k的值为
.
20.如图,点A为函数y=(x>0)图象上一点,连接OA,交函数y=(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为
.
三.解答题
21.已知关于x的反比例函数.
(1)求m的值;
(2)它的图象位于哪些象限?
22.有这样一个问题:探究函数y=的图象与性质.小彤根据学习函数的经验,对函数y=的图象与性质进行了探究.
下面是小彤探究的过程,请补充完整:
(1)函数y=的自变量x的取值范围是
;
(2)下表是y与x的几组对应值:
x
…
﹣2
﹣1
0
1
2
4
5
6
7
8
…
y
…
m
0
﹣1
3
2
…
则m的值为
;
(3)如图所示,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出了图象的一部分,请根据剩余的点补全此函数的图象;
(4)观察图象,写出该函数的一条性质
;
(5)若函数y=的图象上有三个点A(x1,y1)、B(x2,y2)、C(x3,y3),且x1<3<x2<x3,则y1、y2、y3之间的大小关系为
;
23.小楠是一个乐学习,善思考,爱探究的同学,她对函数的图象和性质进行了探究,请你将下列探究过程补充完整:
(Ⅰ)函数的自变量x的取值范围是
.
(Ⅱ)用描点法画函数图象:
(i)列表:
x
…
﹣5
﹣2
﹣1
0
…
2
3
4
7
…
y
…
a
2
3
b
…
6
3
2
1
…
表中a的值为
,b的值为
.
(ii)描点连线:请在右图画出该图象的另一部分.
(Ⅲ)观察函数图象,得到函数的性质:
当x
时,函数值y随x的增大而
;
当x
时,函数值y随x的增大而减少.
(IV)应用:若≥6,则x的取值范围是
.
24.如图,已知∠AOB=90°,∠OAB=30°,反比例函数y=﹣(x<0)的图象过点B(﹣3,a),反比例函数y=(x>0)的图象过点A.
(1)求a和k的值;
(2)过点B作BC∥x轴,与双曲线y=交于点C.求△OAC的面积.
25.点A是反比例函数y=(x>0)的图象l1上一点,直线AB∥x轴,交反比例函数y=(x>0)的图象l2于点B,直线AC∥y轴,交l2于点C,直线CD∥x轴,交l1于点D.
(1)若点A(1,1),求线段AB和CD的长度;
(2)对于任意的点A(a,b),判断线段AB和CD的大小关系,并证明.
26.如图1,点A(m,6),B(6,1)在反比例函数图象上,作直线AB,连接OA、OB.
(1)求反比例函数的表达式和m的值;
(2)求△AOB的面积;
(3)如图2,E是线段AB上一点,作AD⊥x轴于点D,过点E作x轴的垂线,交反比例函数图象于点F,若EF=AD,求出点E的坐标.
27.在平面直角坐标系xOy中,已知直线y=x与双曲线y=的一个交点是A(2,a).
(1)求k的值;
(2)设点P(m,n)是双曲线y=上不同于A的一点,直线PA与x轴交于点B(b,0).
①若m=1,求b的值;
②若PB=2AB,结合图象,直接写出b的值.
参考答案与试题解析
一.选择题
1.解:A、y=,是y与x2成反比例函数关系,故此选项错误;
B、yx=﹣,y是x的反比例函数,故此选项正确;
C、y=5x+6是一次函数关系,故此选项错误;
D、=,不符合反比例函数关系,故此选项错误.
故选:B.
2.解:把x=1代入y=,得y=3,故A点坐标为(1,3);
∵A、B关于y=x对称,则B点坐标为(3,1);
又∵B和C关于原点对称,
∴C点坐标为(﹣3,﹣1),
∴点C的横坐标为﹣3.
故选:B.
3.解:A、图象经过点(﹣1,3),说法错误;
B、图象在第二、四象限,说法错误;
C、不论x为何值,y>0,说法错误;
D、图象所在的第一象限内,y随x的增大而减小,说法正确;
故选:D.
4.解:∵当x=2时,k1x═,
∴2k1=.
∴=
故选:D.
5.解:由于矩形的另一边长=矩形面积÷一边长,
∴矩形的另一边长y(m)与x的函数关系是y=.
故选:C.
6.解:当x>0时,y==,
∵m<0,
∴图象在第四象限;
当x<0时,y==﹣,
∵m<0,
∴﹣m>0,
∴图象在第三象限;
故选:B.
7.解:设△OAC和△BAD的直角边长分别为a、b,
则点B的坐标为(a+b,a﹣b).
∵点B在反比例函数的第一象限图象上,
∴(a+b)×(a﹣b)=a2﹣b2=k.
∴S△OAC﹣S△BAD=a2﹣b2=(a2﹣b2)=.
故选:C.
8.解:设反比例函数的解析式为:y=(x≥8),
则将(8,80),代入得:y=,
故当车速度为20千米/时,则20=,
解得:x=32,
故高架桥上每百米拥有车的数量x应该满足的范围是:x≤32.
故选:B.
9.解:将点A(﹣1,y1),B(2,y2),C(3,y3)分别代入y=﹣得,
y1=5,y2=﹣3,y3=﹣2,
故y2<y3<y1.
故选:A.
10.解:∵函数的图象经过点(3,﹣4),
∴k=3×(﹣4)=﹣12,
符合题意的只有C:k=﹣12×1=﹣12.
故选:C.
二.填空题
11.解:∵y=x2m﹣1是反比例函数,
∴2m﹣1=﹣1,
解之得:m=0.
故答案为0.
12.解:∵正比例函数与反比例函数的图象均关于原点对称,
∴两函数的交点关于原点对称,
∵一个交点的坐标是(2,1),
∴另一个交点的坐标是(﹣2,﹣1).
故答案为:(﹣2,﹣1).
13.解:设反比例函数解析式为y=(k≠0),
将(25,6)代入解析式得,k=25×6=150,
则函数解析式为y=(x≥15),
当y=2时,=2,
解得x=75.
答:从消毒开始,师生至少在75分钟内不能进入教室.
14.解:∵反比例函数y=﹣中,k=﹣(k2+1)<0,
∴此函数的图象在二、四象限,在每一象限内y随x的增大而增大,
∵﹣1<0<2<,
∴y1>0>y3>y2,
故答案为y1>y3>y2.
15.解:由题意知,k=﹣3×2=﹣6.
故答案为:﹣6.
16.解:由题意得:人数x与完成任务所需的时间y之间的函数关系式为y=300÷15x=.
故本题答案为:y=.
17.解:过点E作EG⊥OA,垂足为G,设点B关于EF的对称点为D,连接ED、DF,如图所示:
则△BEF≌△DEF,
∴BF=DF,BE=DE,∠FDE=∠FBE=90°,
∴∠EDG+∠ADF=∠ADF+∠AFD,
∴∠EDG=∠AFD,
∵∠EGD=∠DAF,
∴△ADF∽△GED,
∴=,
∴AD:EG=BF:BE,
∵A(8,0),B(8,4),C(0,4),
∴AB=OC=EG=4,OA=BC=8,
∵E、F在反比例函数y=的图象上,
∴E(,4)、F(8,)
∴OG=EC=,AF=,
∴BF=4﹣,BE=8﹣,
∴====,
∴AD=EG=2,
在Rt△ADF中,由勾股定理:AD2+AF2=DF2
即:22+()2=(4﹣)2
解得:k=12,
故答案为12.
18.解:∵函数y1=kx+b(k、b是常数,且k≠0)与反比例函数y2=(c是常数,且c≠0)的图象相交于A(﹣3,﹣2),B(2,3)两点
∴以﹣3和2为大小的分界点,﹣3<x<0,x>2是y1函数图象都在y2函数图象的上方,
∴y1>y2
故答案为:﹣3<x<0,x>2.
19.解:连接AC分别交BD、x轴于点E、F.
由已知,A、B横坐标分别为1,4,
∴BE=3,
∵四边形ABCD为菱形,AC、BD为对角线
∴S菱形ABCD=4×AE?BE=,
∴AE=,设点B的坐标为(4,y),则A点坐标为(1,y+)
∵点A、B同在y=图象上
∴4y=1?(y+)
∴y=,
∴B点坐标为(4,)
∴k=5
故答案为5.
20.解:设点A的坐标为(a,),点B的坐标为(b,),
∵点C是x轴上一点,且AO=AC,
∴点C的坐标是(2a,0),
设过点O(0,0),A(a,)的直线的解析式为:y=kx,
∴,
解得,k=,
又∵点B(b,)在y=上,
∴,解得,或(舍去),
∴S△ABC=S△AOC﹣S△OBC==,
故答案为:6.
三.解答题
21.解:(1)∵是关于x的反比例函数,
∴m2﹣5=﹣1,且m﹣2≠0,
∴m的值是﹣2;
(2)当m=﹣2时,m﹣2=﹣2﹣2=﹣4<0,
∴这个反比例函数的图像位于第二、四象限.
22.解:(1)∵x﹣3≠0,
∴x≠3;
(2)当x=﹣1时,y===;
(3)如图所示:
(4)由图象可得,当x>3时,y随x的增大而减小(答案不唯一);
(5)由图象可得,当x1<3时,y1<1;当3<x2<x3时,1<y3<y2.
∴y1、y2、y3之间的大小关系为y1<y3<y2.
故答案为:x≠3;;当x>3时,y随x的增大而减小;y1<y3<y2.
23.解:(Ⅰ)x﹣1≠0,解得x≠1,
故答案为x≠1;
(Ⅱ)(i)当x=﹣5时,a=y==1,b=y==6,
故答案为1,6;
(ii)描点后画出如下函数图象:
(Ⅲ)观察函数图象,得到函数的性质:
当x<1时,函数值y随x的增大而增大;
当x>1时,函数值y随x的增大而减少.
故答案为<1,增大;>1;
(Ⅳ)由图象可知,≥6时x的取值范围是0≤x<1或1<x≤2,
故答案为0≤x<1或1<x≤2.
24.解:(1)∵比例函数y=﹣(x<0)的图象过点B(﹣3,a),
∴a=﹣=1,
∴OE=3,BE=1,
分别过点A、B作AD⊥x轴于D,BE⊥x轴于E,
∴∠BOE+∠OBE=90°,
∵∠AOB=90°,∠OAB=30°,
∴∠BOE+∠AOD=90°,tan30°==,
∴∠OBE=∠AOD,
∵∠OEB=∠ADO=90°,
∴△BOE∽△OAD
∴===,
∴AD=?OE==3,OD=?BE==
∴A(,3),
∵反比例函数y=(x>0)的图象过点A,
∴k=×=9;
(2)由(1)可知
AD=3,OD=,
∵BC∥x轴,B(﹣3,1),
∴C点的纵坐标为1,
过点C作CF⊥x轴于F,
∵点C在双曲线y=上,
∴1=,解得x=9,
∴C(9,1),
∴CF=1,
∴S△AOC=S△AOD+S梯形ADFC﹣S△COF=S梯形ADCF
=(AD+CF)(OF﹣OD)
=(3+1)(9﹣)
=13.
25.解:(1)∵AB∥x轴,A(1,1),B在反比例函数的图象上,
∴B(3,1).
同理可求:C(1,3),D(,3).
∴AB=2,CD=.
(2)AB>CD.
证明:∵A(a,b),A在反比例函数的图象上,
∴A(a,).
∵AB∥x轴,B在反比例函数的图象上,
∴B(3a,).
同理可求:C(a,),D(,).
∴AB=2a,CD=.
∵a>0,
∴2a>.
∴AB>CD.
26.解:(1)设反比例函数的解析式为y=,
将B(6,1)的坐标代入y=,得k=6.
∴反比例函数的解析式为y=.
将A(m,6)的坐标代入y=,得m=1.
(2)如图1,设直线AB的解析式为y=ax+b,
把A(1,6)和B(6,1)代入上式,得
,
解得:,
故直线AB的解析式为:y=﹣x+7,
∴M(0,7),N(7,0),
∴S△AOB=S△MON﹣S△AOM﹣S△BON=OM×ON﹣OM×|xA|﹣ON×|yB|
=×7×7﹣×7×1﹣×7×1
=.
(3)设E点的坐标为(m,﹣m+7),则F(m,),
∴EF=﹣m+7﹣.
∵EF=AD,
∴﹣m+7﹣=×6.
解得m1=2,m2=3,
经检验,m1=2,m2=3是分式方程的根,
∴E的坐标为(2,5)或(3,4).
27.解:(1)∵直线y=x与双曲线y=的一个交点是A(2,a),
∴a=×2=1,
∴A(2,1),
∴k=2×1=2;
(2)①若m=1,则P(1,n),
∵点P(1,n)是双曲线y=上不同于A的一点,
∴n=k=2,
∴P(1,2),
∵A(2,1),
则直线PA的解析式为y=﹣x+3,
∵直线PA与x轴交于点B(b,0),
∴0=﹣b+3,
∴b=3;
②如图1,当P在第一象限时,
∵PB=2AB,A(2,1),
∴P点的纵坐标时2,
代入y=求得x=1,
∴P(1,2),
由①可知,此时b=3;
如图2,当P在第,三象限时,
∵PB=2AB,A(2,1),
∴P点的纵坐标时﹣2,
代入y=求得x=﹣1,
∴P(﹣1,﹣2),
∵A(2,1)
则直线PA的解析式为y=x﹣1,
∴b=1,
综上,b的值为3或1.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
