6.4用一次函数解决问题 苏科版数学八年级上册课件(16张)
文档属性
| 名称 | 6.4用一次函数解决问题 苏科版数学八年级上册课件(16张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-09 08:42:13 | ||
图片预览




文档简介
(共16张PPT)
6.4用一次函数解决问题
学习目标
1.从给定的信息中抽象出一次函数关系;
2.求一次函数的关系式;
3.利用一次函数的图像与性质解决实际问题,并注意自变量的取值范围。
请大声地读出来
例:小明乘汽车从相距90千米的甲地前往乙地送文件,到达乙地停留一段时间后返回甲地。如图是小明与甲地的距离y(千米)与出发时间x(时)之间的函数图象。
(1)求y与x之间的函数关系式,并写出自变量x的取值范围。
从图中你能读出哪些信息?
——求函数关系式
典型例题
读图的时候要先明确横纵坐标所表示的实际意义。
看图找点
,见形想式,建模求解。
解:解法一:设OA的函数关系式:y=k1x
把A(1,90)代入得,k1=90
∴OA:y=90x
设BC的函数关系式:y=k2x+b
把B(1.5,90)、C(3,0)代入
得,1.5k2+b=90
解得
k2=
-60
3k2+b=0
,
b=180
∴BC:y=
-60x+180
综上,
90x
0
≤x
≤1
y=
90
1<x≤1.5
-60x+180
1.5≤3
典型例题
——待定系数法求函数关系式
1.设对应的函数关系式
2.代入关键点,求解
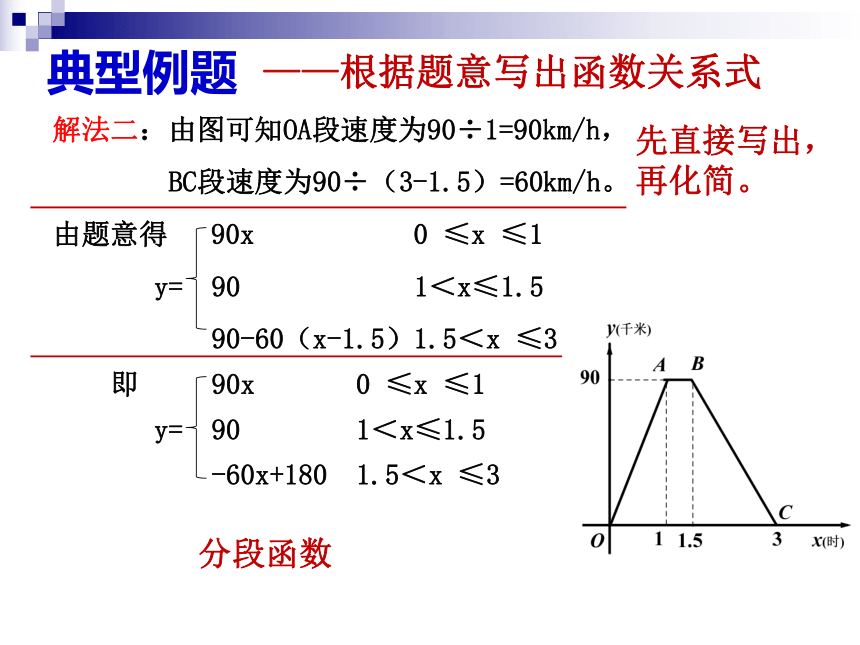
——根据题意写出函数关系式
解法二:由图可知OA段速度为90÷1=90km/h,
BC段速度为90÷(3-1.5)=60km/h。
由题意得
90x
0
≤x
≤1
y=
90
1<x≤1.5
90-60(x-1.5)1.5<x
≤3
即
90x
0
≤x
≤1
y=
90
1<x≤1.5
-60x+180
1.5<x
≤3
分段函数
典型例题
先直接写出,再化简。
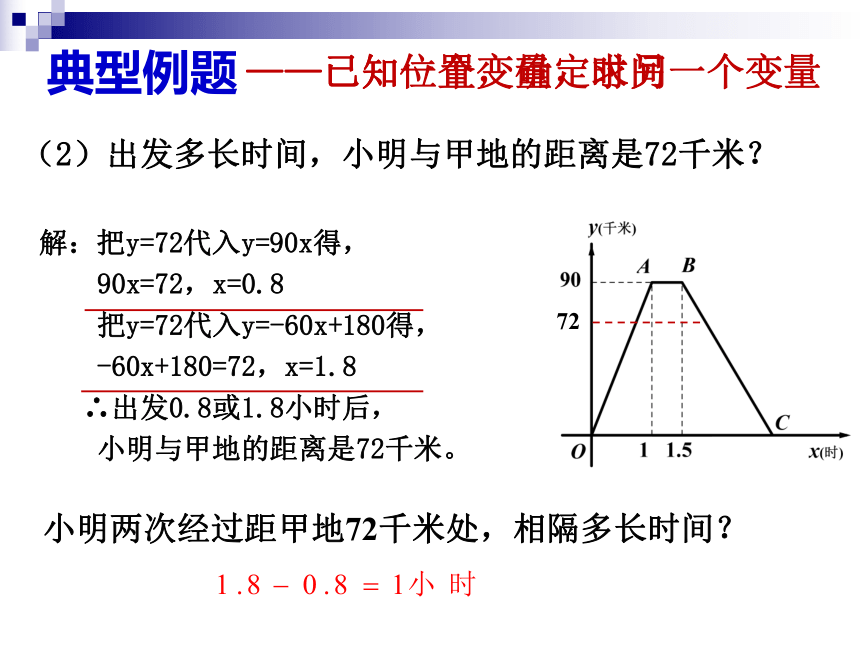
(2)出发多长时间,小明与甲地的距离是72千米?
典型例题
——已知一个变量,求另一个变量
解:把y=72代入y=90x得,
90x=72,x=0.8
把y=72代入y=-60x+180得,
-60x+180=72,x=1.8
∴出发0.8或1.8小时后,
小明与甲地的距离是72千米。
小明两次经过距甲地72千米处,相隔多长时间?
72
——已知位置,确定时间
t+1.2
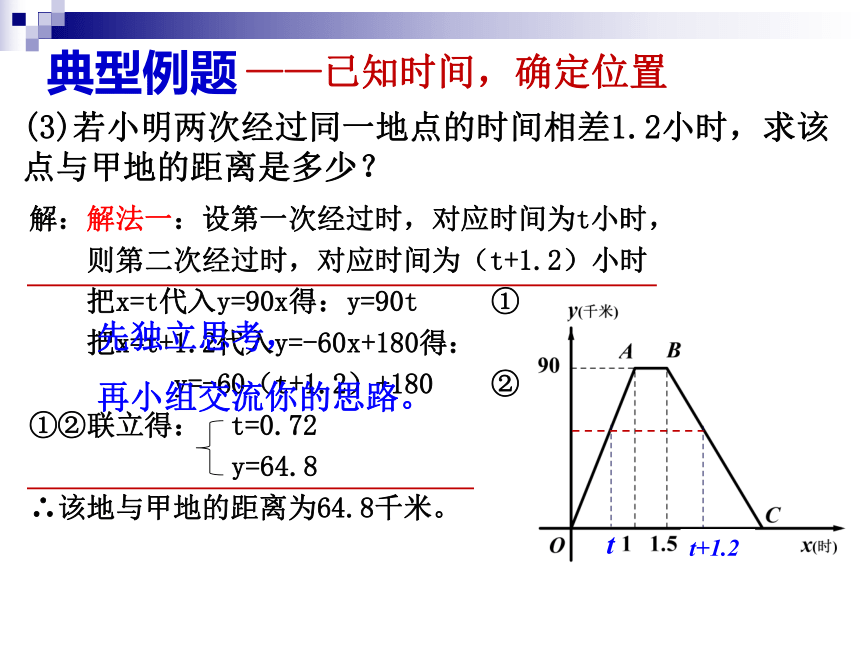
解:解法一:设第一次经过时,对应时间为t小时,
则第二次经过时,对应时间为(t+1.2)小时
把x=t代入y=90x得:y=90t
①
把x=t+1.2代入y=-60x+180得:
y=-60(t+1.2)+180
②
①②联立得:
t=0.72
y=64.8
∴该地与甲地的距离为64.8千米。
t
典型例题
(3)若小明两次经过同一地点的时间相差1.2小时,求该点与甲地的距离是多少?
——已知时间,确定位置
先独立思考,
再小组交流你的思路。
解法二:设两次经过这一地点,在图像上对应点D、E,
延长OA、CB交于点M,作MG⊥DE于点G,交AB于点F
则AB=1.5-1=0.5,DE=1.2
联立
y=90x
解得
x=1.2
y=-60x+180,
y=108
∴M(1.2,108),MF=108-90=18
由题可知△MAB相似于△MDE,
∴
,
,FG=25.2
∴该地与甲地的距离为90-25.2=64.8千米。
t+1.2
t
典型例题
(3)若小明两次经过同一地点的时间相差1.2小时,求该点与甲地的距离是多少?
——已知时间,确定位置
D
E
M
F
G
解法三:在路程一定的情况下,速度与时间成反比
∵由(1)知DA段与BE段的速度之比为3:2,
∴DA段与BE段的时间之比为2:3
设每一份对应时间为m小时,
则
2m+0.5+3m=1.2
m=0.14
∴t=1-2×0.14=0.72
把t=0.72代入y=90x得,y=64.8
∴该地与甲地的距离为64.8千米。
典型例题
(3)若小明两次经过同一地点的时间相差1.2小时,求该点与甲地的距离是多少?
——已知时间,确定位置
t+1.2
t
D
E
解法四:由y=90x1,得x1=
y,
由y=-60x2+180,得x2=-
y+3
∵两次经过此地时间相差1.2h,
∴
x2-
x1=1.2
(-
y+3)-
y=1.2
y=64.8
∴该地与甲地的距离为64.8千米
x1
x2
典型例题
——已知时间,确定位置
(4)同一时刻,小华骑摩托车从甲地前往乙地,匀速行驶。若小华出发2小时后与小明相遇,在同一坐标系内画出小华与甲地的距离y2与时间x的函数图象
,求出y2与x的函数关系式,及小华从甲地到乙地所用的时间。
——交点的意义
y2(小华)
y1(小明)
D
典型例题
E
解:把x=2代入y=-60x+180得,
y=-60×2+180=60
∴点D的坐标是(2,60)
设y2=k3x,把D(2,60)代入得
2k3=60,k3=30
∴y2=30x
把y2=90代入得,x=3
∴小华从甲地到乙地用了3小时。
独立思考
——数形结合
y2(小华)
y1(小明)
D(2,60)
典型例题
(5)在(4)的条件下,经过多长时间,2人相距20千米?
E
—交流讨论
—写出答案
y2(小华)
y1(小明)
D(2,60)
典型例题
E
——数形结合
y2(小华)
y1(小明)
D(2,60)
典型例题
E
——数形结合
这节课你有哪些收获?
回顾总结
读图找点-见形想式-建模求解
1.从给定的信息中抽象出一次函数关系;
2.确定一次函数的关系式;
4.理解交点的意义。
待定系数法
、根据题意直接写出函数关系式
5.数形结合探索解题思路。
3.已知一个变量求另一个变量。
把生活问题抽象成数学问题,再用数学知识解决。
(6)若小明出发0.5小时后,小华骑摩托车从甲地前往乙地,若小华出发1.5小时后与小明相遇,在同一坐标系内画出小华与甲地的距离y2与时间x的函数图像,并求出经过多长时间,2人相距20千米?
y1(小明)
课后作业
6.4用一次函数解决问题
学习目标
1.从给定的信息中抽象出一次函数关系;
2.求一次函数的关系式;
3.利用一次函数的图像与性质解决实际问题,并注意自变量的取值范围。
请大声地读出来
例:小明乘汽车从相距90千米的甲地前往乙地送文件,到达乙地停留一段时间后返回甲地。如图是小明与甲地的距离y(千米)与出发时间x(时)之间的函数图象。
(1)求y与x之间的函数关系式,并写出自变量x的取值范围。
从图中你能读出哪些信息?
——求函数关系式
典型例题
读图的时候要先明确横纵坐标所表示的实际意义。
看图找点
,见形想式,建模求解。
解:解法一:设OA的函数关系式:y=k1x
把A(1,90)代入得,k1=90
∴OA:y=90x
设BC的函数关系式:y=k2x+b
把B(1.5,90)、C(3,0)代入
得,1.5k2+b=90
解得
k2=
-60
3k2+b=0
,
b=180
∴BC:y=
-60x+180
综上,
90x
0
≤x
≤1
y=
90
1<x≤1.5
-60x+180
1.5
典型例题
——待定系数法求函数关系式
1.设对应的函数关系式
2.代入关键点,求解
——根据题意写出函数关系式
解法二:由图可知OA段速度为90÷1=90km/h,
BC段速度为90÷(3-1.5)=60km/h。
由题意得
90x
0
≤x
≤1
y=
90
1<x≤1.5
90-60(x-1.5)1.5<x
≤3
即
90x
0
≤x
≤1
y=
90
1<x≤1.5
-60x+180
1.5<x
≤3
分段函数
典型例题
先直接写出,再化简。
(2)出发多长时间,小明与甲地的距离是72千米?
典型例题
——已知一个变量,求另一个变量
解:把y=72代入y=90x得,
90x=72,x=0.8
把y=72代入y=-60x+180得,
-60x+180=72,x=1.8
∴出发0.8或1.8小时后,
小明与甲地的距离是72千米。
小明两次经过距甲地72千米处,相隔多长时间?
72
——已知位置,确定时间
t+1.2
解:解法一:设第一次经过时,对应时间为t小时,
则第二次经过时,对应时间为(t+1.2)小时
把x=t代入y=90x得:y=90t
①
把x=t+1.2代入y=-60x+180得:
y=-60(t+1.2)+180
②
①②联立得:
t=0.72
y=64.8
∴该地与甲地的距离为64.8千米。
t
典型例题
(3)若小明两次经过同一地点的时间相差1.2小时,求该点与甲地的距离是多少?
——已知时间,确定位置
先独立思考,
再小组交流你的思路。
解法二:设两次经过这一地点,在图像上对应点D、E,
延长OA、CB交于点M,作MG⊥DE于点G,交AB于点F
则AB=1.5-1=0.5,DE=1.2
联立
y=90x
解得
x=1.2
y=-60x+180,
y=108
∴M(1.2,108),MF=108-90=18
由题可知△MAB相似于△MDE,
∴
,
,FG=25.2
∴该地与甲地的距离为90-25.2=64.8千米。
t+1.2
t
典型例题
(3)若小明两次经过同一地点的时间相差1.2小时,求该点与甲地的距离是多少?
——已知时间,确定位置
D
E
M
F
G
解法三:在路程一定的情况下,速度与时间成反比
∵由(1)知DA段与BE段的速度之比为3:2,
∴DA段与BE段的时间之比为2:3
设每一份对应时间为m小时,
则
2m+0.5+3m=1.2
m=0.14
∴t=1-2×0.14=0.72
把t=0.72代入y=90x得,y=64.8
∴该地与甲地的距离为64.8千米。
典型例题
(3)若小明两次经过同一地点的时间相差1.2小时,求该点与甲地的距离是多少?
——已知时间,确定位置
t+1.2
t
D
E
解法四:由y=90x1,得x1=
y,
由y=-60x2+180,得x2=-
y+3
∵两次经过此地时间相差1.2h,
∴
x2-
x1=1.2
(-
y+3)-
y=1.2
y=64.8
∴该地与甲地的距离为64.8千米
x1
x2
典型例题
——已知时间,确定位置
(4)同一时刻,小华骑摩托车从甲地前往乙地,匀速行驶。若小华出发2小时后与小明相遇,在同一坐标系内画出小华与甲地的距离y2与时间x的函数图象
,求出y2与x的函数关系式,及小华从甲地到乙地所用的时间。
——交点的意义
y2(小华)
y1(小明)
D
典型例题
E
解:把x=2代入y=-60x+180得,
y=-60×2+180=60
∴点D的坐标是(2,60)
设y2=k3x,把D(2,60)代入得
2k3=60,k3=30
∴y2=30x
把y2=90代入得,x=3
∴小华从甲地到乙地用了3小时。
独立思考
——数形结合
y2(小华)
y1(小明)
D(2,60)
典型例题
(5)在(4)的条件下,经过多长时间,2人相距20千米?
E
—交流讨论
—写出答案
y2(小华)
y1(小明)
D(2,60)
典型例题
E
——数形结合
y2(小华)
y1(小明)
D(2,60)
典型例题
E
——数形结合
这节课你有哪些收获?
回顾总结
读图找点-见形想式-建模求解
1.从给定的信息中抽象出一次函数关系;
2.确定一次函数的关系式;
4.理解交点的意义。
待定系数法
、根据题意直接写出函数关系式
5.数形结合探索解题思路。
3.已知一个变量求另一个变量。
把生活问题抽象成数学问题,再用数学知识解决。
(6)若小明出发0.5小时后,小华骑摩托车从甲地前往乙地,若小华出发1.5小时后与小明相遇,在同一坐标系内画出小华与甲地的距离y2与时间x的函数图像,并求出经过多长时间,2人相距20千米?
y1(小明)
课后作业
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
