5.7节三角函数的运用-【新教材】人教A版(2019)高中数学必修第一册课后练习(Word含答案)
文档属性
| 名称 | 5.7节三角函数的运用-【新教材】人教A版(2019)高中数学必修第一册课后练习(Word含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 176.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-09 12:58:29 | ||
图片预览

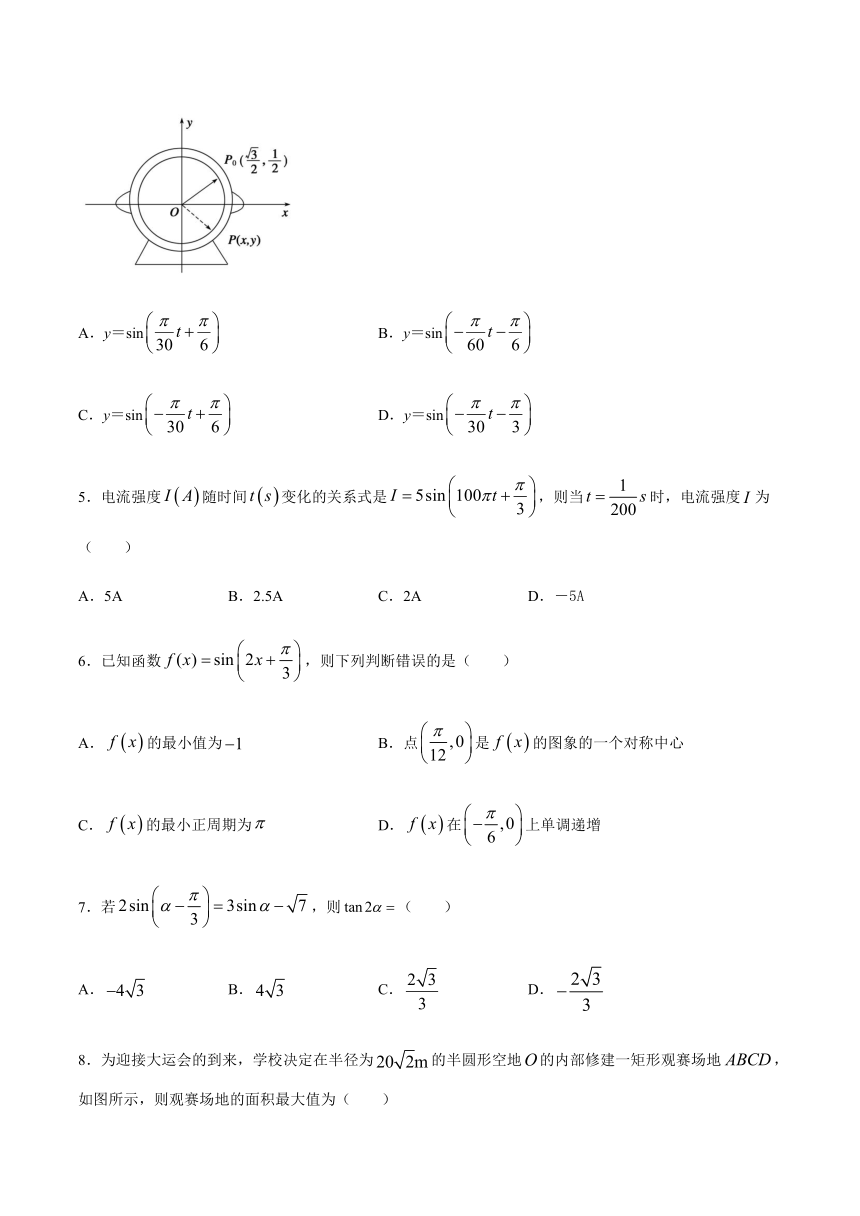


文档简介
12179300124587002020-2021学年第一学期人教A版(2019)必修第一册5.7节三角函数的运用课后练习
一、单选题
1.已知某人的血压满足函数解析式false,其中false为血压,false为时间,则此人每分钟心跳的次数为( )
A.60 B.70 C.80 D.90
2.某艺术展览馆在开馆时间段(9:00—16:00)的参观人数(单位:千)随时间false(单位:时)的变化近似满足函数关系false,且下午两点整参观人数为7千,则开馆中参观人数的最大值为( )
A.1万 B.9千 C.8千 D.7千
3.如图所示为一质点做简谐运动的图象,则下列判断中正确的是( )
A.该质点的振动周期为false B.该质点的振幅为false
C.该质点在false和false时振动速度最大 D.该质点在false和false时的振动速度为0
4.如图,为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针尖位置P(x,y).若初始位置为P0false,当秒针从P0(注:此时t=0)正常开始走时,那么点P的纵坐标y与时间t的函数关系式为( )
A.y=sinfalse B.y=sinfalse
C.y=sinfalse D.y=sinfalse
5.电流强度false随时间false变化的关系式是false,则当false时,电流强度false为( )
A.5A B.2.5A C.2A D.-5A
6.已知函数false,则下列判断错误的是( )
A.false的最小值为false B.点false是false的图象的一个对称中心
C.false的最小正周期为false D.false在false上单调递增
7.若false,则false( )
A.false B.false C.false D.false
8.为迎接大运会的到来,学校决定在半径为false的半圆形空地false的内部修建一矩形观赛场地false,如图所示,则观赛场地的面积最大值为( )
A.400false B. false
C.600false D.800false
二、填空题
9.一根长lcm的线,一端固定,另一端悬挂一个小球,小球摆动时离开平衡位置的位移s(cm)与时间t(s)的函数关系式为false,其中false是重力加速度,当小球摆动的周期是1s时,线长l=________ cm.
10.若将函数false的图象向左平移false个单位后,所得图象对应的函数为偶函数,则实数false的最小值是________.
11.函数false,若存在false,使得对任意false都有false成立,则false的最小值是_____________.
12.关于函数f(x)=false有如下四个命题:
①f(x)的图像关于y轴对称.
②f(x)的图像关于原点对称.
③f(x)的图像关于直线x=false对称.
④f(x)的最小值为2.
其中所有真命题的序号是__________.
解答题
13.如图,半径为4m的水轮绕着圆心O逆时针做匀速圆周运动,每分钟转动4圈,水轮圆心O距离水面2m,如果当水轮上点P从离开水面的时刻(P0)开始计算时间.
(1)将点P距离水面的高度y(m)与时间t(s)满足的函数关系;
(2)求点P第一次到达最高点需要的时间.
14.受日月引力影响,海水会发生涨退潮现象.通常情况下,船在涨潮时驶进港口,退潮时离开港口.某港口在某季节每天港口水位的深度y(米)是时间 t ( 0≤t≤24 ,单位:小时, t=0 表示0:00—零时)的函数,其函数关系式为 y=f(t), f(t)=Asin(ωt+φ)+K (A>0,ω>0,|φ|<π2) .已知一天中该港口水位的深度变化有如下规律:出现相邻两次最高水位的深度的时间差为12小时,最高水位的深度为12米,最低水位的深度为6米,每天13:00时港口水位的深度恰为10.5米.
(1)试求函数 y=f(t) 的表达式;
(2)某货船的吃水深度(船底与水面的距离)为7米,安全条例规定船舶航行时船底与海底的距离不小于15.5米是安全的,问该船在当天的什么时间段能够安全进港?若该船欲于当天安全离港,则它最迟应在当天几点以前离开港口?
16.如图,AOB是一块半径为r的扇形空地, ∠AOB=π2 .某单位计划在空地上修建一个矩形的活动场地OCDE及一矩形停车场EFGH,剩余的地方进行绿化.若 ∠BOG=π6 ,设 ∠AOD=θ
(Ⅰ)记活动场地与停车场占地总面积为 f(θ) ,求 f(θ) 的表达式;
(Ⅱ)当 cosθ 为何值时,可使活动场地与停车场占地总面积最大.
17.如图:某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(Rt△FHE,H是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米,AD=10 3 米,记∠BHE=θ.
(1)试将污水净化管道的长度L表示为θ的函数,并写出定义域;
(2)问:当θ取何值时,污水净化效果最好?并求出此时管道的长度.
参考答案
C2.B3.B4.C5.B6.B7.A8.D9.false10.3 11.2 12.②③
13.【答案】 (1)解:以O为原点建立如图所示的直角坐标系.
由于水轮绕着圆心O做匀速圆周运动,可设点P到水面的距离y(m)与时间t(s)满足函数关系 y=Asin(?t+?)+2,(?π2∵水轮每分钟旋转4圈,
∴ T=604=15 .
∴ ?=2πT=2π15 .
∵水轮半径为4 m,
∴A=4.
∴ y=4sin(2π15t+?)+2,(?π2当t=0时,y=0.
∴ ?=?π6 .
∴ y=4sin(2π15t?π6)+2 .
(2)解:由于最高点距离水面的距离为6,
∴ 6=4sin(2π15t?π6)+2 .
∴ sin(2π15t?π6)=1 .
∴ 2π15t?π6=π2+2kπ(k∈Z) .
∴t=5+15k(k∈Z).
∴当k=0时,即t=5(s)时,点P第一次达到最高点.
【解析】(1)设点P到水面的距离y(m)与时间t(s)满足函数关系 y=Asin(?t+?)+2,(?π214.【答案】 (1)解:依题意, A+K=12,?A+K=6,2πω=12 ,∴ A=3,K=9 , ω=π6 ,又 f(13)=10.5 ,∴ 3sin(13π6+φ)+9=10.5 ,∴ sin(π6+φ)=12 ,又 ?π2<φ<π2 ,∴ φ=0 ,∴ y=f(t)=3sinπ6t+9
(2)解:令 3sinπ6t+9≥7+3.5 得 sinπ6t≥12 ,∴ 2kπ+π6≤π6t≤2kπ+5π6 ,∴ 12k+1≤t≤12k+5,k∈Z
∵ 0≤t≤24 ,∴ 1≤t≤5 或 13≤t≤17 ,∴该船当天安全进港的时间为1~5点和13~17点,最迟应在当天的17点以前离开港口
【解析】(1)最高水位为A+K,最低水位为-A+K,联立方程组求得A和K的值,再由出现相邻两次最高水位的深度的时间差为12小时,可知周期为12,由此求得ω值,再结合每天13:00时港口水位的深度恰为10.5米,把点(13,10.5)代入y=Asin(ωx+φ)+K的解析式求得φ,则函数y=f(t)的表达式可求;(2)直接由(1)中求得的函数表达式大于等于7+3.5求解t的范围,则答案可求.
15.【答案】 解: ( Ⅰ ) 由题意得,在矩形OCDE中, ∠AOD=θ , ∴OC=rcosθ , OE=rsinθ ,
∴ 矩形OCDE的面积为 S矩形OCDE=OC?OE=r2sinθcosθ ;
又 ∠BOG=π6 ,四边形EFGH是矩形, ∴HG=rsinπ6=r2 , OH=rcosπ6=3r2 ,
∴HE=OH?OE=r(32?sinθ) ;
∴ 矩形EFGH的面积为 S矩形EFGH=HG?HE=r22(32?sinθ) ,
∴f(θ)=S矩形OCDE+S矩形EFGH=r2sinθcosθ+r22(32?sinθ)=r2(sinθcosθ?12sinθ+34) ,其中 θ∈(0,π3) ;
( Ⅱ ) 由题意知, f'(θ)=r2(cos2θ?sin2θ?12cosθ)=r22(4cos2θ?cosθ?2) ,
令 f'(θ)=0 ,得 4cos2θ?cosθ?2=0 ,
解得 cosθ=1+338 ,或 cosθ=1?338( 不合题意,舍去 ) ;
令 cosθ0=1+338 ,则 θ0∈(0,π3) ;
① 当 θ∈(0,θ0) 时, f'(θ)>0 , f(θ) 单调递增;
② 当 θ∈(θ0,π3) 时, f'(θ)<0 , f(θ) 单调递减;
∴ 当 θ=θ0 时, f(θ) 取得最大值;
即 cosθ=1+338 时,可使活动场地与停车场占地总面积最大.
【解析】 ( Ⅰ )根据三角函数的定义及矩形的面积公式,即可确定函数的表达式;
(Ⅱ) 求导数,利用导数研究函数的单调性,即可求出函数的最值和此时的余弦值.
16.【答案】 (1)解:由题意可得EH= 10cosθ ,FH= 10sinθ ,EF= 10sinθcosθ ,由于 BE=10tanθ≤10 3 ,AF= 10tanθ ≤10 3 ,
而且 33 ≤tanθ≤ 3 ,θ∈[ π6 , π3 ],
∴L= 10cosθ + 10sinθ + 10sinθcosθ ,θ∈[ π6 , π3 ].
即L=10× sinθ+cosθ+1sinθ?cosθ ,θ∈[ π6 , π3 ]
(2)解:设sinθ+cosθ=t,则 sinθcosθ= t2?12 ,由于θ∈[ π6 , π3 ],∴sinθ+cosθ=t= 2 sin(θ+ π4 )∈[ 3+12 , 2 ].
由于L= 20t?1 ?在[ 3+12 , 2 ]上是单调减函数,∴当t= 3+12 时,即 θ= π6 ?或θ= π3 ?时,L取得最大值为 20( 3 +1)米
【解析】(1)解直角三角形求得得EH、FH、EF的解析式,再由 L=EH+FH+EF得到污水净化管道的长度L的函数解析式,并注明θ的范围.(2)设sinθ+cosθ=t,根据函数 L= 20t?1 ?在[ 3+12 , 2 ]上是单调减函数,可求得L的最大值.
一、单选题
1.已知某人的血压满足函数解析式false,其中false为血压,false为时间,则此人每分钟心跳的次数为( )
A.60 B.70 C.80 D.90
2.某艺术展览馆在开馆时间段(9:00—16:00)的参观人数(单位:千)随时间false(单位:时)的变化近似满足函数关系false,且下午两点整参观人数为7千,则开馆中参观人数的最大值为( )
A.1万 B.9千 C.8千 D.7千
3.如图所示为一质点做简谐运动的图象,则下列判断中正确的是( )
A.该质点的振动周期为false B.该质点的振幅为false
C.该质点在false和false时振动速度最大 D.该质点在false和false时的振动速度为0
4.如图,为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针尖位置P(x,y).若初始位置为P0false,当秒针从P0(注:此时t=0)正常开始走时,那么点P的纵坐标y与时间t的函数关系式为( )
A.y=sinfalse B.y=sinfalse
C.y=sinfalse D.y=sinfalse
5.电流强度false随时间false变化的关系式是false,则当false时,电流强度false为( )
A.5A B.2.5A C.2A D.-5A
6.已知函数false,则下列判断错误的是( )
A.false的最小值为false B.点false是false的图象的一个对称中心
C.false的最小正周期为false D.false在false上单调递增
7.若false,则false( )
A.false B.false C.false D.false
8.为迎接大运会的到来,学校决定在半径为false的半圆形空地false的内部修建一矩形观赛场地false,如图所示,则观赛场地的面积最大值为( )
A.400false B. false
C.600false D.800false
二、填空题
9.一根长lcm的线,一端固定,另一端悬挂一个小球,小球摆动时离开平衡位置的位移s(cm)与时间t(s)的函数关系式为false,其中false是重力加速度,当小球摆动的周期是1s时,线长l=________ cm.
10.若将函数false的图象向左平移false个单位后,所得图象对应的函数为偶函数,则实数false的最小值是________.
11.函数false,若存在false,使得对任意false都有false成立,则false的最小值是_____________.
12.关于函数f(x)=false有如下四个命题:
①f(x)的图像关于y轴对称.
②f(x)的图像关于原点对称.
③f(x)的图像关于直线x=false对称.
④f(x)的最小值为2.
其中所有真命题的序号是__________.
解答题
13.如图,半径为4m的水轮绕着圆心O逆时针做匀速圆周运动,每分钟转动4圈,水轮圆心O距离水面2m,如果当水轮上点P从离开水面的时刻(P0)开始计算时间.
(1)将点P距离水面的高度y(m)与时间t(s)满足的函数关系;
(2)求点P第一次到达最高点需要的时间.
14.受日月引力影响,海水会发生涨退潮现象.通常情况下,船在涨潮时驶进港口,退潮时离开港口.某港口在某季节每天港口水位的深度y(米)是时间 t ( 0≤t≤24 ,单位:小时, t=0 表示0:00—零时)的函数,其函数关系式为 y=f(t), f(t)=Asin(ωt+φ)+K (A>0,ω>0,|φ|<π2) .已知一天中该港口水位的深度变化有如下规律:出现相邻两次最高水位的深度的时间差为12小时,最高水位的深度为12米,最低水位的深度为6米,每天13:00时港口水位的深度恰为10.5米.
(1)试求函数 y=f(t) 的表达式;
(2)某货船的吃水深度(船底与水面的距离)为7米,安全条例规定船舶航行时船底与海底的距离不小于15.5米是安全的,问该船在当天的什么时间段能够安全进港?若该船欲于当天安全离港,则它最迟应在当天几点以前离开港口?
16.如图,AOB是一块半径为r的扇形空地, ∠AOB=π2 .某单位计划在空地上修建一个矩形的活动场地OCDE及一矩形停车场EFGH,剩余的地方进行绿化.若 ∠BOG=π6 ,设 ∠AOD=θ
(Ⅰ)记活动场地与停车场占地总面积为 f(θ) ,求 f(θ) 的表达式;
(Ⅱ)当 cosθ 为何值时,可使活动场地与停车场占地总面积最大.
17.如图:某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(Rt△FHE,H是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米,AD=10 3 米,记∠BHE=θ.
(1)试将污水净化管道的长度L表示为θ的函数,并写出定义域;
(2)问:当θ取何值时,污水净化效果最好?并求出此时管道的长度.
参考答案
C2.B3.B4.C5.B6.B7.A8.D9.false10.3 11.2 12.②③
13.【答案】 (1)解:以O为原点建立如图所示的直角坐标系.
由于水轮绕着圆心O做匀速圆周运动,可设点P到水面的距离y(m)与时间t(s)满足函数关系 y=Asin(?t+?)+2,(?π2∵水轮每分钟旋转4圈,
∴ T=604=15 .
∴ ?=2πT=2π15 .
∵水轮半径为4 m,
∴A=4.
∴ y=4sin(2π15t+?)+2,(?π2当t=0时,y=0.
∴ ?=?π6 .
∴ y=4sin(2π15t?π6)+2 .
(2)解:由于最高点距离水面的距离为6,
∴ 6=4sin(2π15t?π6)+2 .
∴ sin(2π15t?π6)=1 .
∴ 2π15t?π6=π2+2kπ(k∈Z) .
∴t=5+15k(k∈Z).
∴当k=0时,即t=5(s)时,点P第一次达到最高点.
【解析】(1)设点P到水面的距离y(m)与时间t(s)满足函数关系 y=Asin(?t+?)+2,(?π214.【答案】 (1)解:依题意, A+K=12,?A+K=6,2πω=12 ,∴ A=3,K=9 , ω=π6 ,又 f(13)=10.5 ,∴ 3sin(13π6+φ)+9=10.5 ,∴ sin(π6+φ)=12 ,又 ?π2<φ<π2 ,∴ φ=0 ,∴ y=f(t)=3sinπ6t+9
(2)解:令 3sinπ6t+9≥7+3.5 得 sinπ6t≥12 ,∴ 2kπ+π6≤π6t≤2kπ+5π6 ,∴ 12k+1≤t≤12k+5,k∈Z
∵ 0≤t≤24 ,∴ 1≤t≤5 或 13≤t≤17 ,∴该船当天安全进港的时间为1~5点和13~17点,最迟应在当天的17点以前离开港口
【解析】(1)最高水位为A+K,最低水位为-A+K,联立方程组求得A和K的值,再由出现相邻两次最高水位的深度的时间差为12小时,可知周期为12,由此求得ω值,再结合每天13:00时港口水位的深度恰为10.5米,把点(13,10.5)代入y=Asin(ωx+φ)+K的解析式求得φ,则函数y=f(t)的表达式可求;(2)直接由(1)中求得的函数表达式大于等于7+3.5求解t的范围,则答案可求.
15.【答案】 解: ( Ⅰ ) 由题意得,在矩形OCDE中, ∠AOD=θ , ∴OC=rcosθ , OE=rsinθ ,
∴ 矩形OCDE的面积为 S矩形OCDE=OC?OE=r2sinθcosθ ;
又 ∠BOG=π6 ,四边形EFGH是矩形, ∴HG=rsinπ6=r2 , OH=rcosπ6=3r2 ,
∴HE=OH?OE=r(32?sinθ) ;
∴ 矩形EFGH的面积为 S矩形EFGH=HG?HE=r22(32?sinθ) ,
∴f(θ)=S矩形OCDE+S矩形EFGH=r2sinθcosθ+r22(32?sinθ)=r2(sinθcosθ?12sinθ+34) ,其中 θ∈(0,π3) ;
( Ⅱ ) 由题意知, f'(θ)=r2(cos2θ?sin2θ?12cosθ)=r22(4cos2θ?cosθ?2) ,
令 f'(θ)=0 ,得 4cos2θ?cosθ?2=0 ,
解得 cosθ=1+338 ,或 cosθ=1?338( 不合题意,舍去 ) ;
令 cosθ0=1+338 ,则 θ0∈(0,π3) ;
① 当 θ∈(0,θ0) 时, f'(θ)>0 , f(θ) 单调递增;
② 当 θ∈(θ0,π3) 时, f'(θ)<0 , f(θ) 单调递减;
∴ 当 θ=θ0 时, f(θ) 取得最大值;
即 cosθ=1+338 时,可使活动场地与停车场占地总面积最大.
【解析】 ( Ⅰ )根据三角函数的定义及矩形的面积公式,即可确定函数的表达式;
(Ⅱ) 求导数,利用导数研究函数的单调性,即可求出函数的最值和此时的余弦值.
16.【答案】 (1)解:由题意可得EH= 10cosθ ,FH= 10sinθ ,EF= 10sinθcosθ ,由于 BE=10tanθ≤10 3 ,AF= 10tanθ ≤10 3 ,
而且 33 ≤tanθ≤ 3 ,θ∈[ π6 , π3 ],
∴L= 10cosθ + 10sinθ + 10sinθcosθ ,θ∈[ π6 , π3 ].
即L=10× sinθ+cosθ+1sinθ?cosθ ,θ∈[ π6 , π3 ]
(2)解:设sinθ+cosθ=t,则 sinθcosθ= t2?12 ,由于θ∈[ π6 , π3 ],∴sinθ+cosθ=t= 2 sin(θ+ π4 )∈[ 3+12 , 2 ].
由于L= 20t?1 ?在[ 3+12 , 2 ]上是单调减函数,∴当t= 3+12 时,即 θ= π6 ?或θ= π3 ?时,L取得最大值为 20( 3 +1)米
【解析】(1)解直角三角形求得得EH、FH、EF的解析式,再由 L=EH+FH+EF得到污水净化管道的长度L的函数解析式,并注明θ的范围.(2)设sinθ+cosθ=t,根据函数 L= 20t?1 ?在[ 3+12 , 2 ]上是单调减函数,可求得L的最大值.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
