2021-2022学年青岛新版七年级上册数学《第1章 基本的几何图形》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年青岛新版七年级上册数学《第1章 基本的几何图形》单元测试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 270.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-08 19:53:55 | ||
图片预览


文档简介
2021-2022学年青岛新版七年级上册数学《第1章
基本的几何图形》单元测试卷
一.选择题
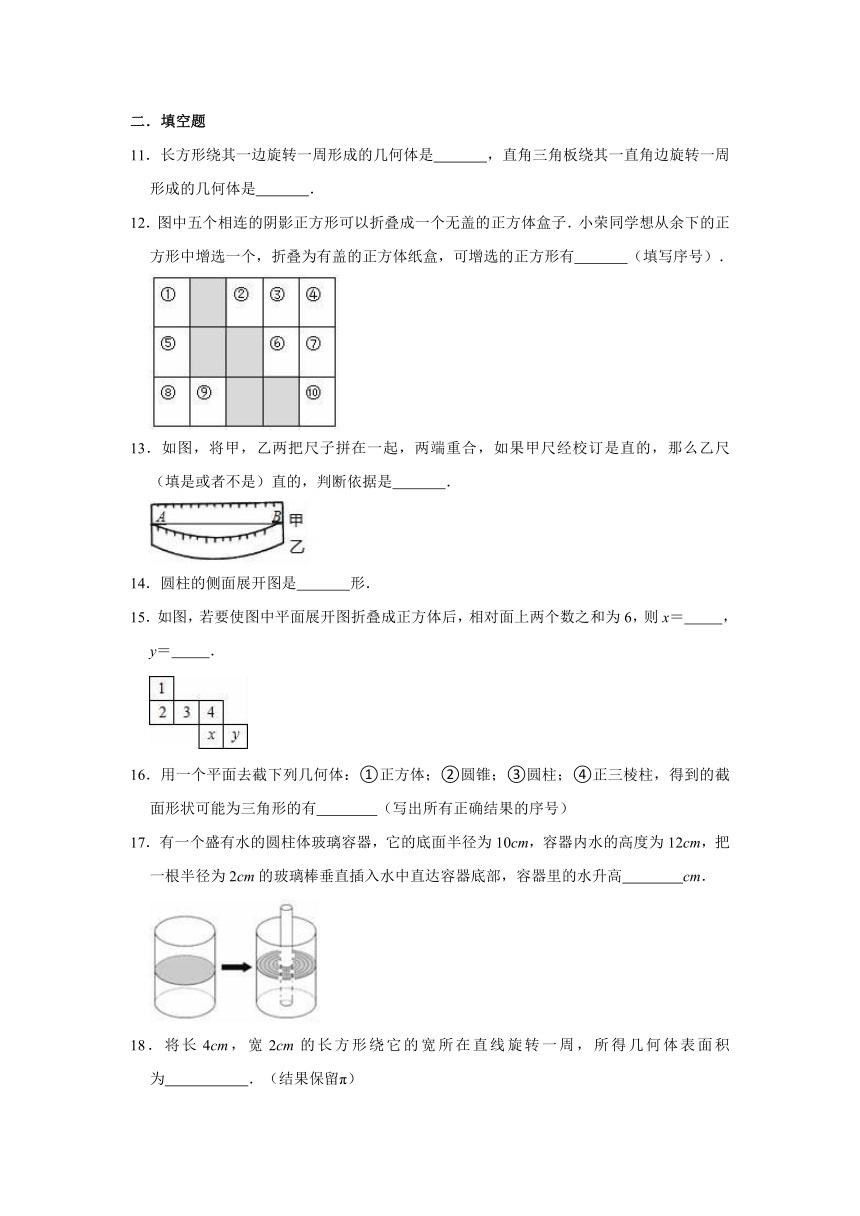
1.将一个正方体的各个面涂上红色或蓝色(可以只用一种颜色),则正方体不同的涂色方案总共有( )种.
A.6
B.8
C.9
D.10
2.直角三角尺绕它的最长边(即斜边)旋转1周,所形成的几何体为( )
A.
B.
C.
D.
3.如图的长方体与下列选项中的立体图形均是由边长为1公分的小正方体紧密堆砌而成.若下列有一立体图形的表面积与如图的表面积相同,则此图形为何?( )
A.
B.
C.
D.
4.如图是某个几何体的平面展开图,该几何体是( )
A.
B.
C.
D.
5.下列说法正确的是( )
A.过一点P只能作一条直线
B.直线AB和直线BA表示同一条直线
C.射线AB和射线BA表示同一条射线
D.射线a比直线b短
6.下列说法中正确的有( )
①过两点有且只有一条直线;
②连接两点的线段叫两点的距离;
③两点之间线段最短;
④若AC=BC,则点C是线段AB的中点.
A.1个
B.2个
C.3个
D.4个
7.一个边长为10厘米的正方形铁丝线圈,若在保持周长不变的情况下把它拉长一个圆,则它的半径为( )厘米.
A.2π
B.
C.
D.10π
8.下面的图形经过折叠可以围成一个棱柱的是( )
A.
B.
C.
D.
9.如图所示的是一个正方体的平面展开图,若将平面展开图折叠成正方体后,相对面上的两个数字之和均为7,则x+y+z的值为( )
A.7
B.8
C.9
D.10
10.如图,用平面去截圆锥,所得截面的形状是( )
A.
B.
C.
D.
二.填空题
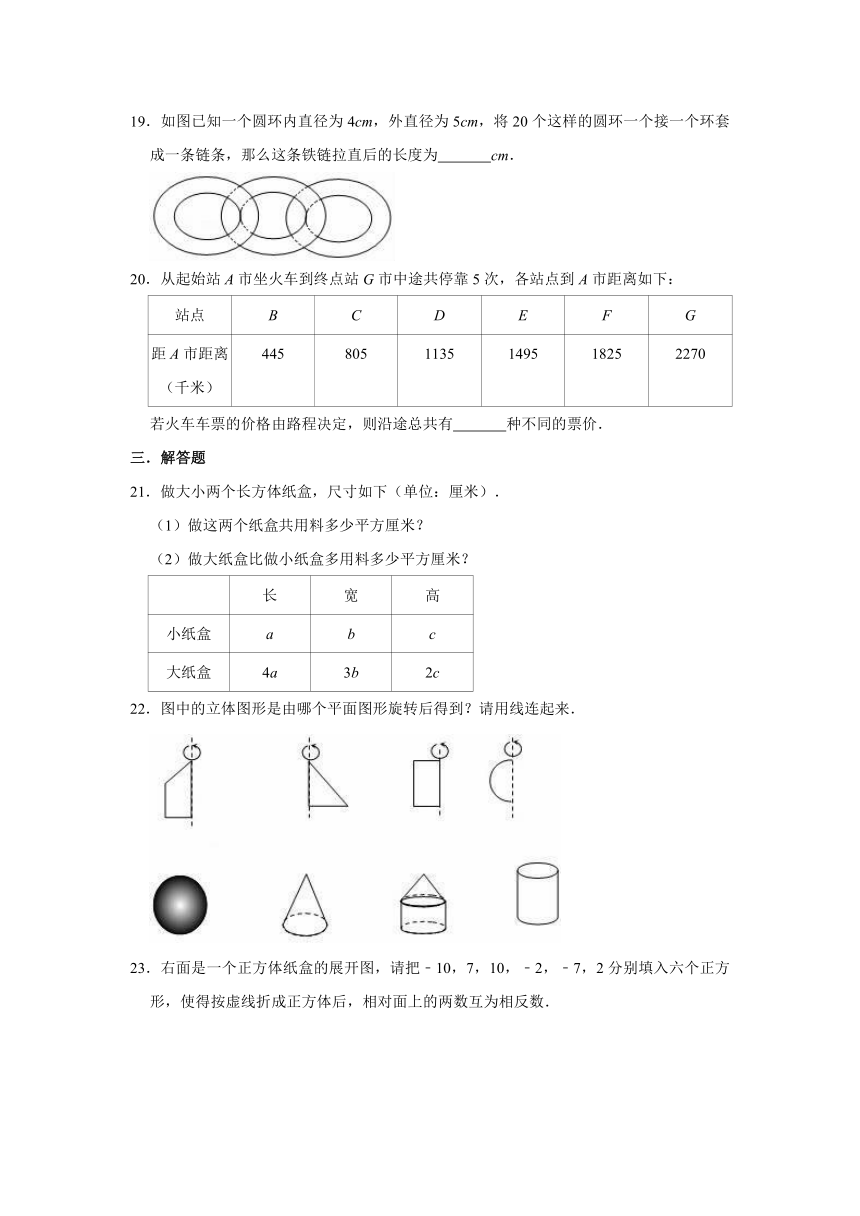
11.长方形绕其一边旋转一周形成的几何体是
,直角三角板绕其一直角边旋转一周形成的几何体是
.
12.图中五个相连的阴影正方形可以折叠成一个无盖的正方体盒子.小荣同学想从余下的正方形中增选一个,折叠为有盖的正方体纸盒,可增选的正方形有
(填写序号).
13.如图,将甲,乙两把尺子拼在一起,两端重合,如果甲尺经校订是直的,那么乙尺
(填是或者不是)直的,判断依据是
.
14.圆柱的侧面展开图是
形.
15.如图,若要使图中平面展开图折叠成正方体后,相对面上两个数之和为6,则x=
,y=
.
16.用一个平面去截下列几何体:①正方体;②圆锥;③圆柱;④正三棱柱,得到的截面形状可能为三角形的有
(写出所有正确结果的序号)
17.有一个盛有水的圆柱体玻璃容器,它的底面半径为10cm,容器内水的高度为12cm,把一根半径为2cm的玻璃棒垂直插入水中直达容器底部,容器里的水升高
cm.
18.将长4cm,宽2cm的长方形绕它的宽所在直线旋转一周,所得几何体表面积为
.(结果保留π)
19.如图已知一个圆环内直径为4cm,外直径为5cm,将20个这样的圆环一个接一个环套成一条链条,那么这条铁链拉直后的长度为
cm.
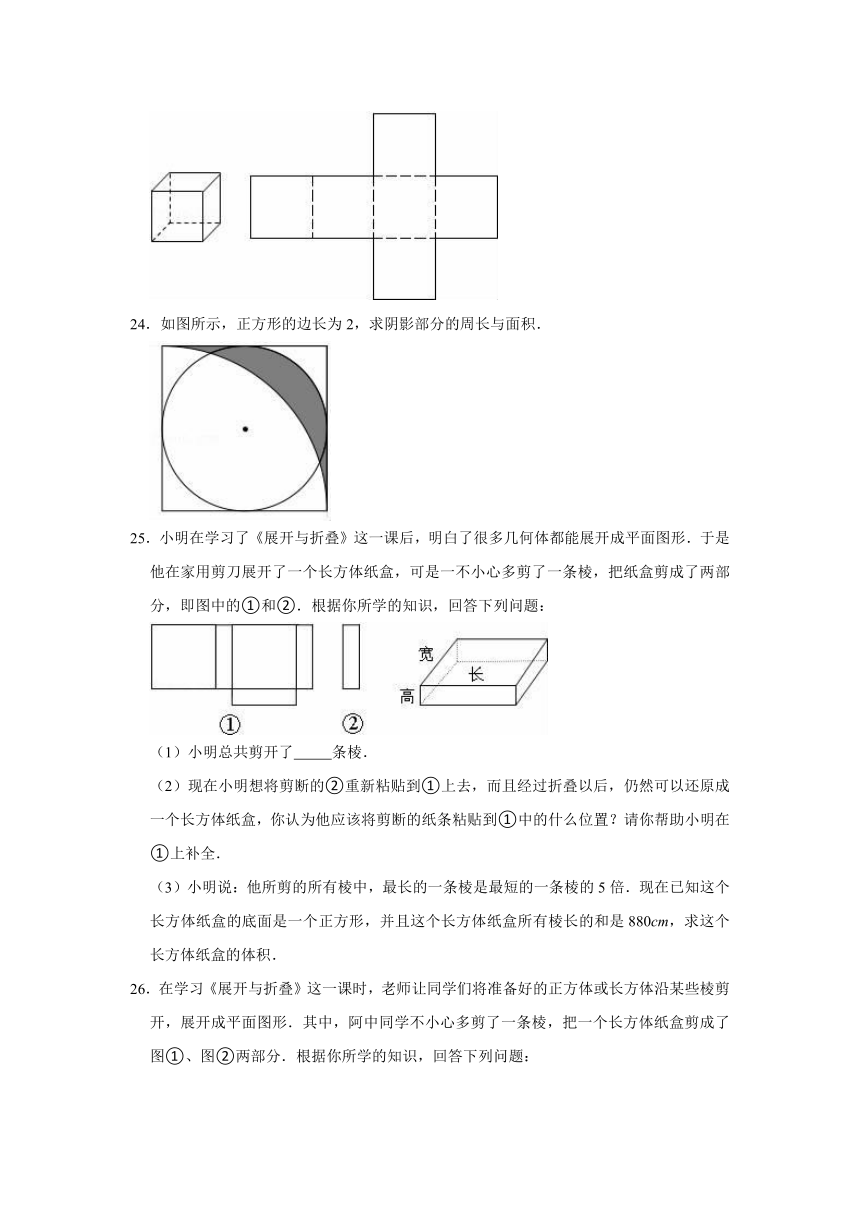
20.从起始站A市坐火车到终点站G市中途共停靠5次,各站点到A市距离如下:
站点
B
C
D
E
F
G
距A市距离(千米)
445
805
1135
1495
1825
2270
若火车车票的价格由路程决定,则沿途总共有
种不同的票价.
三.解答题
21.做大小两个长方体纸盒,尺寸如下(单位:厘米).
(1)做这两个纸盒共用料多少平方厘米?
(2)做大纸盒比做小纸盒多用料多少平方厘米?
长
宽
高
小纸盒
a
b
c
大纸盒
4a
3b
2c
22.图中的立体图形是由哪个平面图形旋转后得到?请用线连起来.
23.右面是一个正方体纸盒的展开图,请把﹣10,7,10,﹣2,﹣7,2分别填入六个正方形,使得按虚线折成正方体后,相对面上的两数互为相反数.
24.如图所示,正方形的边长为2,求阴影部分的周长与面积.
25.小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(1)小明总共剪开了
条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
26.在学习《展开与折叠》这一课时,老师让同学们将准备好的正方体或长方体沿某些棱剪开,展开成平面图形.其中,阿中同学不小心多剪了一条棱,把一个长方体纸盒剪成了图①、图②两部分.根据你所学的知识,回答下列问题:
(1)阿中总共剪开了几条棱?
(2)现在阿中想将剪断的图②重新粘贴到图①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,他有几种粘贴方法?请在图①上画出粘贴后的图形(画出一种即可);
(3)已知图③是阿中剪开的图①的某些数据,求这个长方体纸盒的体积.
27.如图四个几何体分别是三棱柱,四棱柱,五棱柱和六棱柱,三棱柱有5个面,9条棱,6个顶点,观察图形,填写下面的空.
(1)四棱柱有
个面,
条棱,
个顶点;
(2)六棱柱有
个面,
条棱,
个顶点;
(3)由此猜想n棱柱有
个面,
条棱,
个顶点.
参考答案与试题解析
一.选择题
1.解:若只涂红色:1种情况;
若只涂蓝色:1种情况;
若1个面涂红色:1种情况;
若2个面涂红色:2种情况;
若3个面涂红色:2种情况;
若4个面涂红色:2种情况;
若5个面涂红色:1种情况;
共有:1+1+1+2+2+2+2+1=10.
故选:D.
2.解:直角三角尺绕它的最长边(即斜边)旋转1周,所形成的几何体是两个同底且相连的圆锥.
故选:C.
3.解:∵立体图形均是由边长为1公分的小正方体紧密堆砌而成,
∴附图的表面积为:6×2+3×2+2×2=22,
只有选项B的表面积为:5×2+3+4+5=22.
故选:B.
4.解:观察图形可知,这个几何体是三棱柱.
故选:D.
5.解:A、过一点P可以作无数条直线;故A错误.
B、直线可以用两个大写字母来表示,且直线没有方向,所以AB和BA是表示同一条直线;故B正确.
C、射线AB和射线BA,端点不同,方向相反,故射线AB和射线BA表示不同的射线;故C错误.
D、射线和直线不能进行长短的比较;故D错误.
故选:B.
6.解:①过两点有且只有一条直线,正确;
②连接两点的线段的长叫两点的距离,是线段的长,故此选项错误;
③两点之间线段最短,正确;
④若AC=BC,则点C是线段AB的中点,C可能在线段垂直平分线上,故此选项错误.
故选:B.
7.解:由题意可得:10×4÷π÷2
=(厘米),
答:它的半径为厘米;
故选:B.
8.解:选项A不能组成棱柱,是因为上下两底面四个边的长不能与侧面的边等长、重合;
选项C中折叠后没有上底面,不能折成棱柱;
选项D缺少两个底面,不能围成棱柱;
只有B能围成棱柱.
故选:B.
9.解:根据正方体展开图的“相间、Z端是对面”的特征可知,
“﹣2”与“y”相对,
“3”与“z”相对,
“x”与“10”相对,
又∵相对面上的两个数字之和均为7,
∴x=﹣3,y=9,z=4,
∴x+y+z=﹣3+9+4=10,
故选:D.
10.解:用平面取截圆锥,如图:平面与圆锥的侧面截得一条弧线,与底面截得一条直线,所以截面的形状应该是D.
故选:D.
二.填空题
11.解:长方形绕它的一边旋转一周可形成圆柱,直角三角形绕它的直角边旋转一周可形成圆锥.
故答案为圆柱,圆锥.
12.解:如图,只可以增选①或⑤.
故答案为:①⑤.
13.解:∵甲尺是直的,两尺拼在一起两端重合,
∴甲尺经校订是直的,那么乙尺就一定不是直的,
判断依据是:两点确定一条直线.
故答案为:不是,两点确定一条直线.
14.解:圆柱的侧面展开图为长方形.
故答案为:长方.
15.解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“2”与“4”是相对面,
“1”与“x”是相对面,
“3”与“y”是相对面,
∵相对面上两个数之和为6,
∴x=5,y=3.
故答案为:5;3.
16.解:①正方体能截出三角形;
②圆锥沿着母线截几何体可以截出三角形;
③圆柱不能截出三角形;
④正三棱柱能截出三角形.
故截面可能是三角形的有3个.
故答案为:①②④.
17.解:设容器内的水将升高xcm,据题意得:π?102×12+π?22(12+x)=π?102(12+x),1200+4(12+x)=100(12+x),
1200+48+4x=1200+100x,
96x=48,
x=0.5.
即容器内的水将升高0.5cm.
故答案为:0.5.
18.解:将长4cm,宽2cm的长方形绕它的宽所在直线旋转一周,所得几何体是底面半径为4cm,高为3cm的圆柱体,
所以这个圆柱体的表面积为π×42×2+2π×4×2=32π+16π=48πcm2,
故答案为:48πcm2.
19.解:根据题意可知,1个圆环的最长长度是(5﹣4)+4=5(cm);
2个圆环套成的链条拉直后的长度是(5﹣4)+4×2=9(cm);
3个圆环套成的链条拉直后的长度是(5﹣4)+4×3=13(cm);
…
20个圆环套成的链条拉直后的长度是(5﹣4)+4×20=81(cm).
故答案为:81.
20.解:∵①从A分别到B、C、D、E、F、G共6种票价,
如图
BC=805﹣445=360,
CD=1135﹣805=330,
DE=1495﹣1135=360,
EF=1825﹣1495=330,
FG=2270﹣1825=445,
即AB=FG,BC=DE,CD=EF,
②∵BC=360,BD=690,BE=1050,BF=1380,BG=1825=AF,
∴从B出发的有4种票价,有BC、BD、BE、BF,4种;
③∵CD=330,CE=690=BD,CF=1020,CG=1465,
∴从C出发的(除去路程相同的)有3种票价,有CD,CF,CG,3种;
④∵DE=360=BC,DF=690=BD,DG=1135=AD,
∴从D出发的(除去路程相同的)有0种票价;
⑤∵EF=330=CD,EG=775,
∴从E出发的(除去路程相同的)有1种票价,有EG,1种;
⑥∵FG=445=AB,
∴从F出发的(除去路程相同的)有0种票价;
∴6+4+3+0+1+0=14,
故答案为:14.
三.解答题
21.解:(1)做这两个纸盒共用料:
(2ab+2bc+2ac)+(12ab+8ac+6bc)×2,
=2ab+2bc+2ac+24ab+16ac+12bc
=26ab+14bc+18ac(cm2);
∴做这两个纸盒共用料(26ab+14bc+18ac)平方厘米;
(2)做大纸盒比做小纸盒多用料:
2×(12ab+8ac+6bc)﹣(2ab+2bc+2ac)=24ab+12bc+16ac﹣2ab﹣2bc﹣2ac
=22ab+10bc+14ac(cm2);
∴做大纸盒比做小纸盒多用料(22ab+10bc+14ac)平方厘米.
22.解:如图.
23.解:根据相反数的定义将﹣10,7,﹣2分别填到10,﹣7,2的对面(答案不唯一),如:
24.解:(1)l小=πr小=π,
l大=πr大=π×2=π,
l直=1+1=2,
C总=2+l小+l大=2+π+π=2+1.5π;
(2)S正大=4,S扇大=π=π,
S正小=1,S扇小=π=π,
S阴=(S正大﹣S扇大)﹣(S正小﹣S扇小)=3﹣π.
25.解(1)小明共剪了8条棱,
故答案为:8.
(2)如图,四种情况.
(3)∵长方体纸盒的底面是一个正方形,
∴设最短的棱长高为acm,则长与宽相等为5acm,
∵长方体纸盒所有棱长的和是880cm,
∴4(a+5a+5a)=880,解得a=20cm,
∴这个长方体纸盒的体积为:20×100×100=200000立方厘米.
26.解:(1)总共12条棱,其中有4条未剪开,故阿中总共剪开了8条棱.
(2)答:有4种粘贴方法.
如图,四种情况:
(3)设高为xcm,则宽为(4﹣x)cm,长为[7﹣(4﹣x)]=(3+x)cm,
∴4+(3+x)=8,
解得:x=1,
∴体积为:(3+1)×(4﹣1)×1=12(cm3),
答:这个长方形纸盒的体积为12cm3.
27.解:(1)四棱柱有6个面,12条棱,8个顶点;
(2)六棱柱有8个面,18条棱,12个顶点;
(3)由此猜想n棱柱有(n+2)个面,3n条棱,2n个顶点.
故答案为:(1)6,12,8;(2)8,18,12;(3)(n+2),3n,2n.
基本的几何图形》单元测试卷
一.选择题
1.将一个正方体的各个面涂上红色或蓝色(可以只用一种颜色),则正方体不同的涂色方案总共有( )种.
A.6
B.8
C.9
D.10
2.直角三角尺绕它的最长边(即斜边)旋转1周,所形成的几何体为( )
A.
B.
C.
D.
3.如图的长方体与下列选项中的立体图形均是由边长为1公分的小正方体紧密堆砌而成.若下列有一立体图形的表面积与如图的表面积相同,则此图形为何?( )
A.
B.
C.
D.
4.如图是某个几何体的平面展开图,该几何体是( )
A.
B.
C.
D.
5.下列说法正确的是( )
A.过一点P只能作一条直线
B.直线AB和直线BA表示同一条直线
C.射线AB和射线BA表示同一条射线
D.射线a比直线b短
6.下列说法中正确的有( )
①过两点有且只有一条直线;
②连接两点的线段叫两点的距离;
③两点之间线段最短;
④若AC=BC,则点C是线段AB的中点.
A.1个
B.2个
C.3个
D.4个
7.一个边长为10厘米的正方形铁丝线圈,若在保持周长不变的情况下把它拉长一个圆,则它的半径为( )厘米.
A.2π
B.
C.
D.10π
8.下面的图形经过折叠可以围成一个棱柱的是( )
A.
B.
C.
D.
9.如图所示的是一个正方体的平面展开图,若将平面展开图折叠成正方体后,相对面上的两个数字之和均为7,则x+y+z的值为( )
A.7
B.8
C.9
D.10
10.如图,用平面去截圆锥,所得截面的形状是( )
A.
B.
C.
D.
二.填空题
11.长方形绕其一边旋转一周形成的几何体是
,直角三角板绕其一直角边旋转一周形成的几何体是
.
12.图中五个相连的阴影正方形可以折叠成一个无盖的正方体盒子.小荣同学想从余下的正方形中增选一个,折叠为有盖的正方体纸盒,可增选的正方形有
(填写序号).
13.如图,将甲,乙两把尺子拼在一起,两端重合,如果甲尺经校订是直的,那么乙尺
(填是或者不是)直的,判断依据是
.
14.圆柱的侧面展开图是
形.
15.如图,若要使图中平面展开图折叠成正方体后,相对面上两个数之和为6,则x=
,y=
.
16.用一个平面去截下列几何体:①正方体;②圆锥;③圆柱;④正三棱柱,得到的截面形状可能为三角形的有
(写出所有正确结果的序号)
17.有一个盛有水的圆柱体玻璃容器,它的底面半径为10cm,容器内水的高度为12cm,把一根半径为2cm的玻璃棒垂直插入水中直达容器底部,容器里的水升高
cm.
18.将长4cm,宽2cm的长方形绕它的宽所在直线旋转一周,所得几何体表面积为
.(结果保留π)
19.如图已知一个圆环内直径为4cm,外直径为5cm,将20个这样的圆环一个接一个环套成一条链条,那么这条铁链拉直后的长度为
cm.
20.从起始站A市坐火车到终点站G市中途共停靠5次,各站点到A市距离如下:
站点
B
C
D
E
F
G
距A市距离(千米)
445
805
1135
1495
1825
2270
若火车车票的价格由路程决定,则沿途总共有
种不同的票价.
三.解答题
21.做大小两个长方体纸盒,尺寸如下(单位:厘米).
(1)做这两个纸盒共用料多少平方厘米?
(2)做大纸盒比做小纸盒多用料多少平方厘米?
长
宽
高
小纸盒
a
b
c
大纸盒
4a
3b
2c
22.图中的立体图形是由哪个平面图形旋转后得到?请用线连起来.
23.右面是一个正方体纸盒的展开图,请把﹣10,7,10,﹣2,﹣7,2分别填入六个正方形,使得按虚线折成正方体后,相对面上的两数互为相反数.
24.如图所示,正方形的边长为2,求阴影部分的周长与面积.
25.小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(1)小明总共剪开了
条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
26.在学习《展开与折叠》这一课时,老师让同学们将准备好的正方体或长方体沿某些棱剪开,展开成平面图形.其中,阿中同学不小心多剪了一条棱,把一个长方体纸盒剪成了图①、图②两部分.根据你所学的知识,回答下列问题:
(1)阿中总共剪开了几条棱?
(2)现在阿中想将剪断的图②重新粘贴到图①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,他有几种粘贴方法?请在图①上画出粘贴后的图形(画出一种即可);
(3)已知图③是阿中剪开的图①的某些数据,求这个长方体纸盒的体积.
27.如图四个几何体分别是三棱柱,四棱柱,五棱柱和六棱柱,三棱柱有5个面,9条棱,6个顶点,观察图形,填写下面的空.
(1)四棱柱有
个面,
条棱,
个顶点;
(2)六棱柱有
个面,
条棱,
个顶点;
(3)由此猜想n棱柱有
个面,
条棱,
个顶点.
参考答案与试题解析
一.选择题
1.解:若只涂红色:1种情况;
若只涂蓝色:1种情况;
若1个面涂红色:1种情况;
若2个面涂红色:2种情况;
若3个面涂红色:2种情况;
若4个面涂红色:2种情况;
若5个面涂红色:1种情况;
共有:1+1+1+2+2+2+2+1=10.
故选:D.
2.解:直角三角尺绕它的最长边(即斜边)旋转1周,所形成的几何体是两个同底且相连的圆锥.
故选:C.
3.解:∵立体图形均是由边长为1公分的小正方体紧密堆砌而成,
∴附图的表面积为:6×2+3×2+2×2=22,
只有选项B的表面积为:5×2+3+4+5=22.
故选:B.
4.解:观察图形可知,这个几何体是三棱柱.
故选:D.
5.解:A、过一点P可以作无数条直线;故A错误.
B、直线可以用两个大写字母来表示,且直线没有方向,所以AB和BA是表示同一条直线;故B正确.
C、射线AB和射线BA,端点不同,方向相反,故射线AB和射线BA表示不同的射线;故C错误.
D、射线和直线不能进行长短的比较;故D错误.
故选:B.
6.解:①过两点有且只有一条直线,正确;
②连接两点的线段的长叫两点的距离,是线段的长,故此选项错误;
③两点之间线段最短,正确;
④若AC=BC,则点C是线段AB的中点,C可能在线段垂直平分线上,故此选项错误.
故选:B.
7.解:由题意可得:10×4÷π÷2
=(厘米),
答:它的半径为厘米;
故选:B.
8.解:选项A不能组成棱柱,是因为上下两底面四个边的长不能与侧面的边等长、重合;
选项C中折叠后没有上底面,不能折成棱柱;
选项D缺少两个底面,不能围成棱柱;
只有B能围成棱柱.
故选:B.
9.解:根据正方体展开图的“相间、Z端是对面”的特征可知,
“﹣2”与“y”相对,
“3”与“z”相对,
“x”与“10”相对,
又∵相对面上的两个数字之和均为7,
∴x=﹣3,y=9,z=4,
∴x+y+z=﹣3+9+4=10,
故选:D.
10.解:用平面取截圆锥,如图:平面与圆锥的侧面截得一条弧线,与底面截得一条直线,所以截面的形状应该是D.
故选:D.
二.填空题
11.解:长方形绕它的一边旋转一周可形成圆柱,直角三角形绕它的直角边旋转一周可形成圆锥.
故答案为圆柱,圆锥.
12.解:如图,只可以增选①或⑤.
故答案为:①⑤.
13.解:∵甲尺是直的,两尺拼在一起两端重合,
∴甲尺经校订是直的,那么乙尺就一定不是直的,
判断依据是:两点确定一条直线.
故答案为:不是,两点确定一条直线.
14.解:圆柱的侧面展开图为长方形.
故答案为:长方.
15.解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“2”与“4”是相对面,
“1”与“x”是相对面,
“3”与“y”是相对面,
∵相对面上两个数之和为6,
∴x=5,y=3.
故答案为:5;3.
16.解:①正方体能截出三角形;
②圆锥沿着母线截几何体可以截出三角形;
③圆柱不能截出三角形;
④正三棱柱能截出三角形.
故截面可能是三角形的有3个.
故答案为:①②④.
17.解:设容器内的水将升高xcm,据题意得:π?102×12+π?22(12+x)=π?102(12+x),1200+4(12+x)=100(12+x),
1200+48+4x=1200+100x,
96x=48,
x=0.5.
即容器内的水将升高0.5cm.
故答案为:0.5.
18.解:将长4cm,宽2cm的长方形绕它的宽所在直线旋转一周,所得几何体是底面半径为4cm,高为3cm的圆柱体,
所以这个圆柱体的表面积为π×42×2+2π×4×2=32π+16π=48πcm2,
故答案为:48πcm2.
19.解:根据题意可知,1个圆环的最长长度是(5﹣4)+4=5(cm);
2个圆环套成的链条拉直后的长度是(5﹣4)+4×2=9(cm);
3个圆环套成的链条拉直后的长度是(5﹣4)+4×3=13(cm);
…
20个圆环套成的链条拉直后的长度是(5﹣4)+4×20=81(cm).
故答案为:81.
20.解:∵①从A分别到B、C、D、E、F、G共6种票价,
如图
BC=805﹣445=360,
CD=1135﹣805=330,
DE=1495﹣1135=360,
EF=1825﹣1495=330,
FG=2270﹣1825=445,
即AB=FG,BC=DE,CD=EF,
②∵BC=360,BD=690,BE=1050,BF=1380,BG=1825=AF,
∴从B出发的有4种票价,有BC、BD、BE、BF,4种;
③∵CD=330,CE=690=BD,CF=1020,CG=1465,
∴从C出发的(除去路程相同的)有3种票价,有CD,CF,CG,3种;
④∵DE=360=BC,DF=690=BD,DG=1135=AD,
∴从D出发的(除去路程相同的)有0种票价;
⑤∵EF=330=CD,EG=775,
∴从E出发的(除去路程相同的)有1种票价,有EG,1种;
⑥∵FG=445=AB,
∴从F出发的(除去路程相同的)有0种票价;
∴6+4+3+0+1+0=14,
故答案为:14.
三.解答题
21.解:(1)做这两个纸盒共用料:
(2ab+2bc+2ac)+(12ab+8ac+6bc)×2,
=2ab+2bc+2ac+24ab+16ac+12bc
=26ab+14bc+18ac(cm2);
∴做这两个纸盒共用料(26ab+14bc+18ac)平方厘米;
(2)做大纸盒比做小纸盒多用料:
2×(12ab+8ac+6bc)﹣(2ab+2bc+2ac)=24ab+12bc+16ac﹣2ab﹣2bc﹣2ac
=22ab+10bc+14ac(cm2);
∴做大纸盒比做小纸盒多用料(22ab+10bc+14ac)平方厘米.
22.解:如图.
23.解:根据相反数的定义将﹣10,7,﹣2分别填到10,﹣7,2的对面(答案不唯一),如:
24.解:(1)l小=πr小=π,
l大=πr大=π×2=π,
l直=1+1=2,
C总=2+l小+l大=2+π+π=2+1.5π;
(2)S正大=4,S扇大=π=π,
S正小=1,S扇小=π=π,
S阴=(S正大﹣S扇大)﹣(S正小﹣S扇小)=3﹣π.
25.解(1)小明共剪了8条棱,
故答案为:8.
(2)如图,四种情况.
(3)∵长方体纸盒的底面是一个正方形,
∴设最短的棱长高为acm,则长与宽相等为5acm,
∵长方体纸盒所有棱长的和是880cm,
∴4(a+5a+5a)=880,解得a=20cm,
∴这个长方体纸盒的体积为:20×100×100=200000立方厘米.
26.解:(1)总共12条棱,其中有4条未剪开,故阿中总共剪开了8条棱.
(2)答:有4种粘贴方法.
如图,四种情况:
(3)设高为xcm,则宽为(4﹣x)cm,长为[7﹣(4﹣x)]=(3+x)cm,
∴4+(3+x)=8,
解得:x=1,
∴体积为:(3+1)×(4﹣1)×1=12(cm3),
答:这个长方形纸盒的体积为12cm3.
27.解:(1)四棱柱有6个面,12条棱,8个顶点;
(2)六棱柱有8个面,18条棱,12个顶点;
(3)由此猜想n棱柱有(n+2)个面,3n条棱,2n个顶点.
故答案为:(1)6,12,8;(2)8,18,12;(3)(n+2),3n,2n.
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
