不等式
图片预览


文档简介
高二数学同题公开课教案(必修5)
课题:第三章《不等式》的复习(一)
◆教学重点:⒈经历实际情景,复习本章所研究的不等式模型,即一元二次不等式.
⒉会解一元二次不等式;⒊一元二次不等式的应用.
◆教学难点:理解二次函数、一元二次方程与一元二次不等式的关系并能灵活应用;
◆三维目标:
⒈知识与技能
①经历实际情景,复习本章所研究的不等式模型,一元二次不等式.
②会解一元二次不等式;
③灵活运用一元二次不等式.
⒉过程与方法
①采用探究法,按照联想、思考、合作交流、逻辑分析、抽象应用的方法进行启发式教学;
②教师提供问题、素材,并及时点拨,发挥老师的主导作用和学生的主体作用;
③将探索过程设计为较典型的具有挑战性的问题,激发学生去积极思考,从而培养学生的数学学习兴趣.
⒊情感态度与价值观
①通过具体问题的解决,让学生去感受现实世界和日常生活中存在着大量的不等量关系并需要从理性的角度去思考,鼓励学生用数学观点进行归纳、抽象,使学生感受数学、走进数学、培养学生严谨的数学学习习惯和良好的思维习惯.
②学习过程中,通过对问题的探究思考,广泛参与,培养学生严谨的思维习惯,主动、积极的学习品质,从而提高学习质量;
③通过对富有挑战性的问题的解决,激发学生顽强的探究精神和严肃认真的科学态度,同时去感受数学的应用性,体会数学的奥秘,数学的简洁美,数学推理的严谨美,从而激发学生的学习兴趣并树立辩证的世界观.
◆教学过程:
一、复习回顾:
引入:自变量在什么范围取值时,对二次函数的值等于0?大于0?小于0?
提问:结合此实例,请同学们描述一下二次函数、一元二次方程与一元二次不等式有什么关系呢?(结合图形)
二、教师精讲:
由一元二次不等式的一般形式,知任何一个一元二次不等式,最后都可以化为
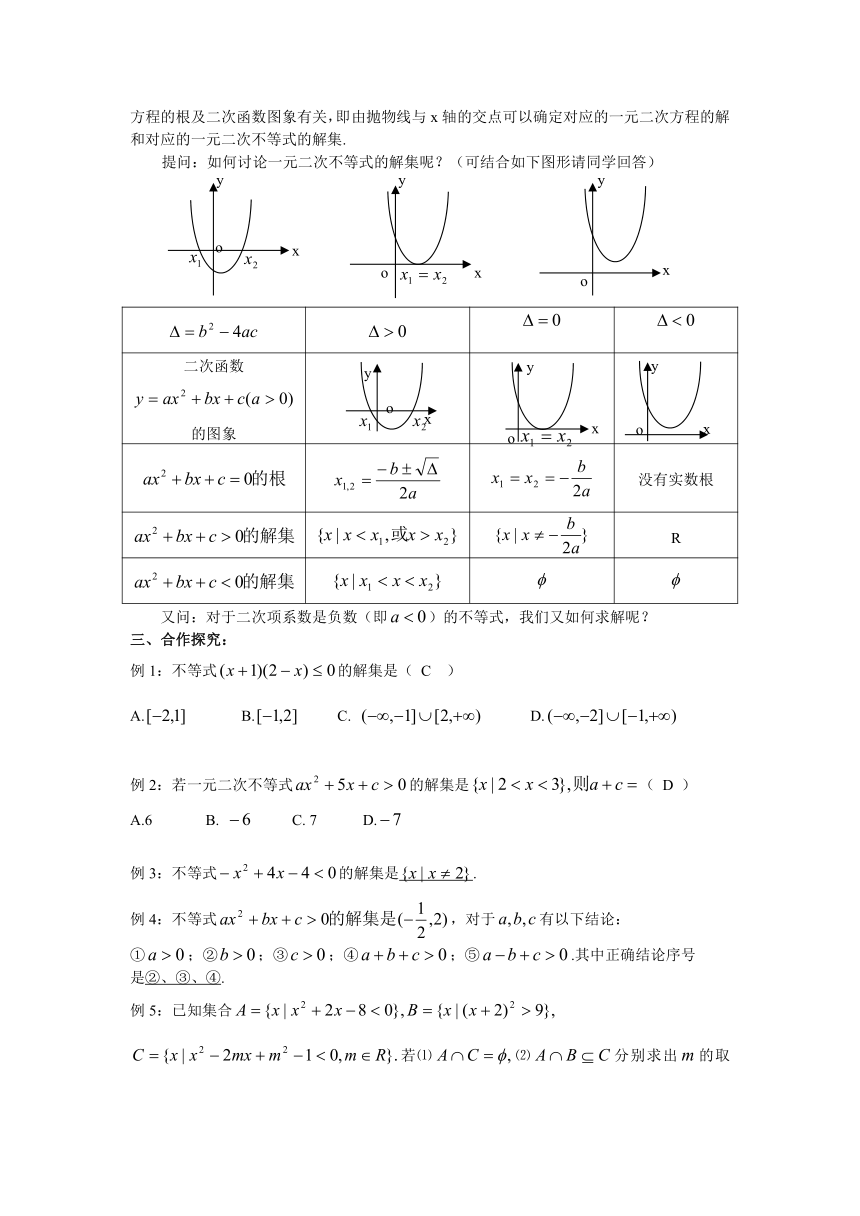
形式.一元二次不等式的解与其相应的一元二次方程的根及二次函数图象有关,即由抛物线与x轴的交点可以确定对应的一元二次方程的解和对应的一元二次不等式的解集.
提问:如何讨论一元二次不等式的解集呢?(可结合如下图形请同学回答)
二次函数的图象
没有实数根
R
又问:对于二次项系数是负数(即)的不等式,我们又如何求解呢?
三、合作探究:
例1:不等式的解集是( C )
A. B. C. D.
例2:若一元二次不等式的解集是( D )
A.6 B. C. 7 D.
例3:不等式的解集是.
例4:不等式,对于有以下结论:
①;②;③;④;⑤.其中正确结论序号
是②、③、④.
例5:已知集合
若⑴⑵分别求出的取值范围. (答案:⑴;⑵)
◆例题点评:
四、课堂练习:
⒈解不等式(组):①; ②
⒉解关于的不等式:
⒊已知不等式①②③要使同时满足①②的也满足③,则有( C )
A. B. C. D.
⒋关于的不等式的解集是,求实数的取值范围.
(答案:)
五、课堂小结:
本节课我们复习了哪些知识、方法?同学们用这些知识、方法解决了什么问题?通过本节课的复习,同学们又有什么收获呢?
六、课后作业:
⒈已知不等式的解集是A,不等式的解集是B,不等式
( A )
A. B. 1 C. D. 3
⒉不等式组有解,则实数的取值范围是( C )
A. B. C. D.
⒊已知关于的方程的两根异号,且负根的绝对值比正根大,那么实数的取值范围是( D )
A. B. C. D.
⒋已知:函数,当时,不等式恒成立,求实数的取值范围. (答案:)
⒌已知:函数是二次函数,不等式的解集为且在区间上的最大值是12,求函数的解析式. (答案:)
⒍已知二次函数的二次项系数为,且不等式的解集为
⑴若有两个相等的实数根,求的解析式.
(答案:)
⑵若的最大值为正数,求实数的取值范围.
(答案:)
七、板书设计:
八、教学反思:
高二数学课堂例题、练习、作业
一、课堂例题
例1:不等式的解集是( )
A. B. C. D.
例2:若一元二次不等式的解集是( )
A.6 B. C. 7 D.
例3:不等式的解集是__________________..
例4:不等式,对于有以下结论:
①;②;③;④;⑤.其中正确结论序号
是___________________________.
例5:已知集合
若⑴⑵分别求出的取值范围.
二、课堂练习:
⒈解不等式(组):①; ②
⒉解关于的不等式:
⒊已知不等式①②③要使同时满足①②的也满足③,则有( )
A. B. C. D.
⒋关于的不等式的解集是,求实数的取值范围.
三、课后作业:
⒈已知不等式的解集是A,不等式的解集是B,不等式
( )
A. B. 1 C. D. 3
⒉不等式组有解,则实数的取值范围是( )
A. B. C. D.
⒊已知关于的方程的两根异号,且负根的绝对值比正根大,那么实数的取值范围是( )
A. B. C. D.
⒋已知:函数,当时,不等式恒成立,求实数的取值范围.
⒌已知:函数是二次函数,不等式的解集为且在区间上的最大值是12,求函数的解析式.
⒍已知二次函数的二次项系数为,且不等式的解集为
⑴若有两个相等的实数根,求的解析式.
⑵若的最大值为正数,求实数的取值范围.
w.w.w.k.s.5.u.c.o.m
www.
x
y
o
x
y
o
x
y
o
y
y
y
x
o
EMBED Equation.3
EMBED Equation.3
x
o
x
o
1.引例:自变量在什么范围取值时,对二次函数的值等于0?大于0?小于0?
2.一元二次不等式:
3.如何讨论一元二次不等式的解集呢?
4.典型例题精讲及方法引导:
5.示范解题:
6.方法归纳:
7.课堂练习:
8.小结:
9.作业:
课题:第三章《不等式》的复习(一)
◆教学重点:⒈经历实际情景,复习本章所研究的不等式模型,即一元二次不等式.
⒉会解一元二次不等式;⒊一元二次不等式的应用.
◆教学难点:理解二次函数、一元二次方程与一元二次不等式的关系并能灵活应用;
◆三维目标:
⒈知识与技能
①经历实际情景,复习本章所研究的不等式模型,一元二次不等式.
②会解一元二次不等式;
③灵活运用一元二次不等式.
⒉过程与方法
①采用探究法,按照联想、思考、合作交流、逻辑分析、抽象应用的方法进行启发式教学;
②教师提供问题、素材,并及时点拨,发挥老师的主导作用和学生的主体作用;
③将探索过程设计为较典型的具有挑战性的问题,激发学生去积极思考,从而培养学生的数学学习兴趣.
⒊情感态度与价值观
①通过具体问题的解决,让学生去感受现实世界和日常生活中存在着大量的不等量关系并需要从理性的角度去思考,鼓励学生用数学观点进行归纳、抽象,使学生感受数学、走进数学、培养学生严谨的数学学习习惯和良好的思维习惯.
②学习过程中,通过对问题的探究思考,广泛参与,培养学生严谨的思维习惯,主动、积极的学习品质,从而提高学习质量;
③通过对富有挑战性的问题的解决,激发学生顽强的探究精神和严肃认真的科学态度,同时去感受数学的应用性,体会数学的奥秘,数学的简洁美,数学推理的严谨美,从而激发学生的学习兴趣并树立辩证的世界观.
◆教学过程:
一、复习回顾:
引入:自变量在什么范围取值时,对二次函数的值等于0?大于0?小于0?
提问:结合此实例,请同学们描述一下二次函数、一元二次方程与一元二次不等式有什么关系呢?(结合图形)
二、教师精讲:
由一元二次不等式的一般形式,知任何一个一元二次不等式,最后都可以化为
形式.一元二次不等式的解与其相应的一元二次方程的根及二次函数图象有关,即由抛物线与x轴的交点可以确定对应的一元二次方程的解和对应的一元二次不等式的解集.
提问:如何讨论一元二次不等式的解集呢?(可结合如下图形请同学回答)
二次函数的图象
没有实数根
R
又问:对于二次项系数是负数(即)的不等式,我们又如何求解呢?
三、合作探究:
例1:不等式的解集是( C )
A. B. C. D.
例2:若一元二次不等式的解集是( D )
A.6 B. C. 7 D.
例3:不等式的解集是.
例4:不等式,对于有以下结论:
①;②;③;④;⑤.其中正确结论序号
是②、③、④.
例5:已知集合
若⑴⑵分别求出的取值范围. (答案:⑴;⑵)
◆例题点评:
四、课堂练习:
⒈解不等式(组):①; ②
⒉解关于的不等式:
⒊已知不等式①②③要使同时满足①②的也满足③,则有( C )
A. B. C. D.
⒋关于的不等式的解集是,求实数的取值范围.
(答案:)
五、课堂小结:
本节课我们复习了哪些知识、方法?同学们用这些知识、方法解决了什么问题?通过本节课的复习,同学们又有什么收获呢?
六、课后作业:
⒈已知不等式的解集是A,不等式的解集是B,不等式
( A )
A. B. 1 C. D. 3
⒉不等式组有解,则实数的取值范围是( C )
A. B. C. D.
⒊已知关于的方程的两根异号,且负根的绝对值比正根大,那么实数的取值范围是( D )
A. B. C. D.
⒋已知:函数,当时,不等式恒成立,求实数的取值范围. (答案:)
⒌已知:函数是二次函数,不等式的解集为且在区间上的最大值是12,求函数的解析式. (答案:)
⒍已知二次函数的二次项系数为,且不等式的解集为
⑴若有两个相等的实数根,求的解析式.
(答案:)
⑵若的最大值为正数,求实数的取值范围.
(答案:)
七、板书设计:
八、教学反思:
高二数学课堂例题、练习、作业
一、课堂例题
例1:不等式的解集是( )
A. B. C. D.
例2:若一元二次不等式的解集是( )
A.6 B. C. 7 D.
例3:不等式的解集是__________________..
例4:不等式,对于有以下结论:
①;②;③;④;⑤.其中正确结论序号
是___________________________.
例5:已知集合
若⑴⑵分别求出的取值范围.
二、课堂练习:
⒈解不等式(组):①; ②
⒉解关于的不等式:
⒊已知不等式①②③要使同时满足①②的也满足③,则有( )
A. B. C. D.
⒋关于的不等式的解集是,求实数的取值范围.
三、课后作业:
⒈已知不等式的解集是A,不等式的解集是B,不等式
( )
A. B. 1 C. D. 3
⒉不等式组有解,则实数的取值范围是( )
A. B. C. D.
⒊已知关于的方程的两根异号,且负根的绝对值比正根大,那么实数的取值范围是( )
A. B. C. D.
⒋已知:函数,当时,不等式恒成立,求实数的取值范围.
⒌已知:函数是二次函数,不等式的解集为且在区间上的最大值是12,求函数的解析式.
⒍已知二次函数的二次项系数为,且不等式的解集为
⑴若有两个相等的实数根,求的解析式.
⑵若的最大值为正数,求实数的取值范围.
w.w.w.k.s.5.u.c.o.m
www.
x
y
o
x
y
o
x
y
o
y
y
y
x
o
EMBED Equation.3
EMBED Equation.3
x
o
x
o
1.引例:自变量在什么范围取值时,对二次函数的值等于0?大于0?小于0?
2.一元二次不等式:
3.如何讨论一元二次不等式的解集呢?
4.典型例题精讲及方法引导:
5.示范解题:
6.方法归纳:
7.课堂练习:
8.小结:
9.作业:
