苏科版数学八年级下册 9.7中心对称图形 平行四边形 小结与思考 教案
文档属性
| 名称 | 苏科版数学八年级下册 9.7中心对称图形 平行四边形 小结与思考 教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 75.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-09 00:00:00 | ||
图片预览

文档简介
平行四边形小结与思考
学习目标 会根据已知点的坐标提出问题,并运用数形结合的思想方法解决问题
分类讨论思想在三角形相似中的应用
运用代数的方法探究特殊平行四边形的存在性问题
教学重点 如何解决由运动产生的面积问题,特殊平行四边形问题。
教学难点 如何将综合型的问题分解成几个小问题,并注意小题之间的联系。
教师活动 学生活动 设计意图
导课:利用物理学家杨振宁的名言引入,近几年的中考题出现了许多新型题型,阅读理解,开放性探究,所以仅仅停留在会解数学题是不够的。
总结:其实所有的问题归结为三类:1、求线段的长;2、求解析式;3、有关三角形问题
强调:分类讨论思想,规范过程书写
几何画板展示:变化的平行四边形。让学生提出问题。
提问:点P坐标为多少时,点P和点E关于X轴对称?
继续追问:这个问题还能怎么问?
多种方法展示发现:方程中根的判别式<0,所以无解,所以不存在平行四边形OPDE是矩形,也就不能是正方形。如果一定要成为矩形,怎么办?
板书过程并总结 一:简单问题,全开放回顾基本知识点
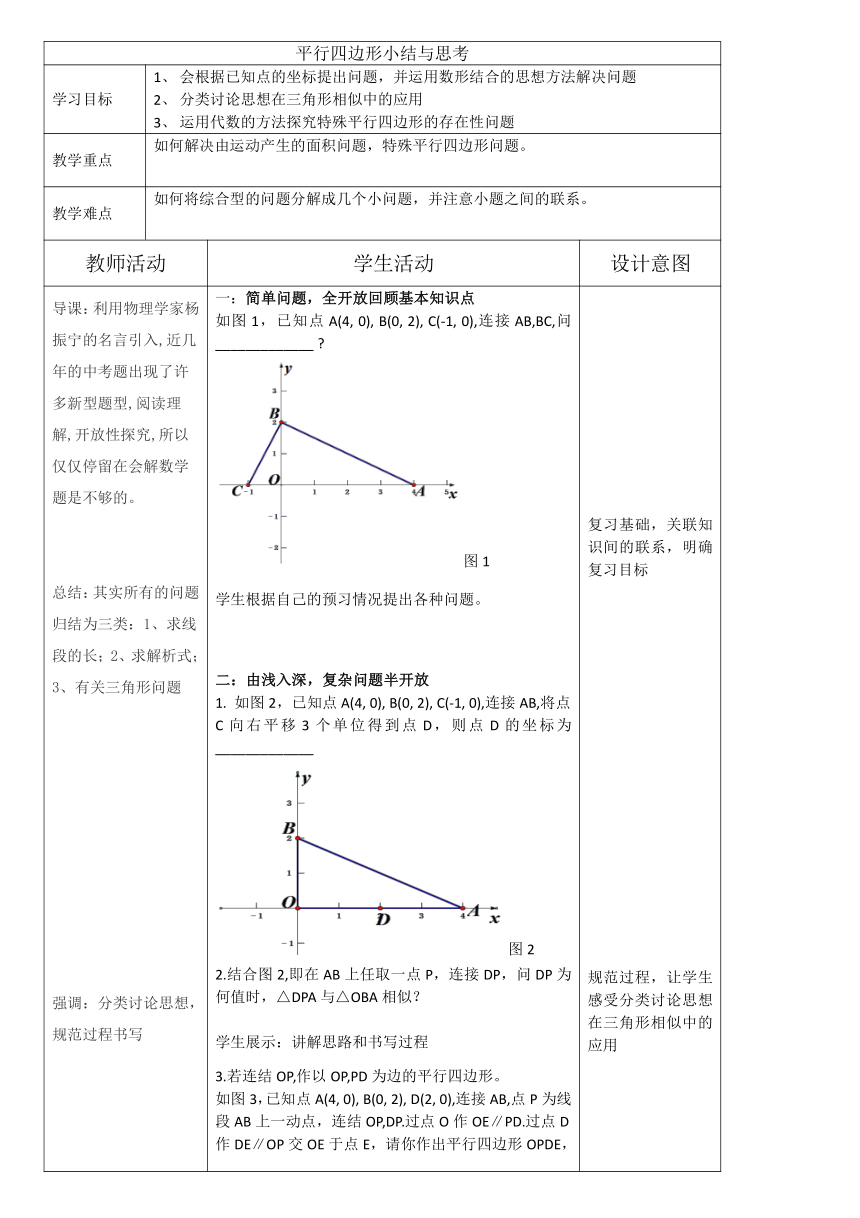
如图1,已知点A(4, 0), B(0, 2), C(-1, 0),连接AB,BC,问 _____________ ?
图1
学生根据自己的预习情况提出各种问题。
二:由浅入深,复杂问题半开放
1. 如图2,已知点A(4, 0), B(0, 2), C(-1, 0),连接AB,将点C向右平移3个单位得到点D,则点D的坐标为_____________
图2
2.结合图2,即在AB上任取一点P,连接DP,问DP为何值时,△DPA与△OBA相似?
学生展示:讲解思路和书写过程
3.若连结OP,作以OP,PD为边的平行四边形。
如图3,已知点A(4, 0), B(0, 2), D(2, 0),连接AB,点P为线段AB上一动点,连结OP,DP.过点O作OE∥PD.过点D作DE∥OP交OE于点E,请你作出平行四边形OPDE, _è????·??????è?????è?????è?????????????????_
图3
同桌互相看画出的平行四边形,发现不一样,得出:有无数个。
问:何时平行四边形面积最大?(学生回答,并阐述理由)
学生讲解
点P坐标为多少时,四边形OPDE是菱形?
学生讲解思路
紧接着学生提出:点P坐标为多少时,四边形OPDE是矩形?正方形?
5分钟时间讨论,小组展示讨论结果
改变D的位置,这样就演变成中考题
7.如图7,已知点A(4, 0), B(0, 2), D(m, 0),连结AB,点P为线段AB上一动点,连结OP,DP.过点O作OE∥PD.过点D作DE∥OP交OE于点E,当0<m<4时,若存在唯一位置使得平行四边形OPDE是矩形,求此时m的值。
根据刚才的方法就可以解决。
三.通过本节课的探究,你的收获及所达成的目标
学生自由总结
四、作业
当点P坐标为多少时,点E落在y轴上?
当点P坐标为多少时,OP=2EO?
复习基础,关联知识间的联系,明确复习目标
规范过程,让学生感受分类讨论思想在三角形相似中的应用
充分发挥学生的主体地位,让学生自己提出问题,自己解决问题
由特殊到一般,找到解决办法
让学生真正体会收获
学习目标 会根据已知点的坐标提出问题,并运用数形结合的思想方法解决问题
分类讨论思想在三角形相似中的应用
运用代数的方法探究特殊平行四边形的存在性问题
教学重点 如何解决由运动产生的面积问题,特殊平行四边形问题。
教学难点 如何将综合型的问题分解成几个小问题,并注意小题之间的联系。
教师活动 学生活动 设计意图
导课:利用物理学家杨振宁的名言引入,近几年的中考题出现了许多新型题型,阅读理解,开放性探究,所以仅仅停留在会解数学题是不够的。
总结:其实所有的问题归结为三类:1、求线段的长;2、求解析式;3、有关三角形问题
强调:分类讨论思想,规范过程书写
几何画板展示:变化的平行四边形。让学生提出问题。
提问:点P坐标为多少时,点P和点E关于X轴对称?
继续追问:这个问题还能怎么问?
多种方法展示发现:方程中根的判别式<0,所以无解,所以不存在平行四边形OPDE是矩形,也就不能是正方形。如果一定要成为矩形,怎么办?
板书过程并总结 一:简单问题,全开放回顾基本知识点
如图1,已知点A(4, 0), B(0, 2), C(-1, 0),连接AB,BC,问 _____________ ?
图1
学生根据自己的预习情况提出各种问题。
二:由浅入深,复杂问题半开放
1. 如图2,已知点A(4, 0), B(0, 2), C(-1, 0),连接AB,将点C向右平移3个单位得到点D,则点D的坐标为_____________
图2
2.结合图2,即在AB上任取一点P,连接DP,问DP为何值时,△DPA与△OBA相似?
学生展示:讲解思路和书写过程
3.若连结OP,作以OP,PD为边的平行四边形。
如图3,已知点A(4, 0), B(0, 2), D(2, 0),连接AB,点P为线段AB上一动点,连结OP,DP.过点O作OE∥PD.过点D作DE∥OP交OE于点E,请你作出平行四边形OPDE, _è????·??????è?????è?????è?????????????????_
图3
同桌互相看画出的平行四边形,发现不一样,得出:有无数个。
问:何时平行四边形面积最大?(学生回答,并阐述理由)
学生讲解
点P坐标为多少时,四边形OPDE是菱形?
学生讲解思路
紧接着学生提出:点P坐标为多少时,四边形OPDE是矩形?正方形?
5分钟时间讨论,小组展示讨论结果
改变D的位置,这样就演变成中考题
7.如图7,已知点A(4, 0), B(0, 2), D(m, 0),连结AB,点P为线段AB上一动点,连结OP,DP.过点O作OE∥PD.过点D作DE∥OP交OE于点E,当0<m<4时,若存在唯一位置使得平行四边形OPDE是矩形,求此时m的值。
根据刚才的方法就可以解决。
三.通过本节课的探究,你的收获及所达成的目标
学生自由总结
四、作业
当点P坐标为多少时,点E落在y轴上?
当点P坐标为多少时,OP=2EO?
复习基础,关联知识间的联系,明确复习目标
规范过程,让学生感受分类讨论思想在三角形相似中的应用
充分发挥学生的主体地位,让学生自己提出问题,自己解决问题
由特殊到一般,找到解决办法
让学生真正体会收获
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
