平行线的特征

(共25张PPT)
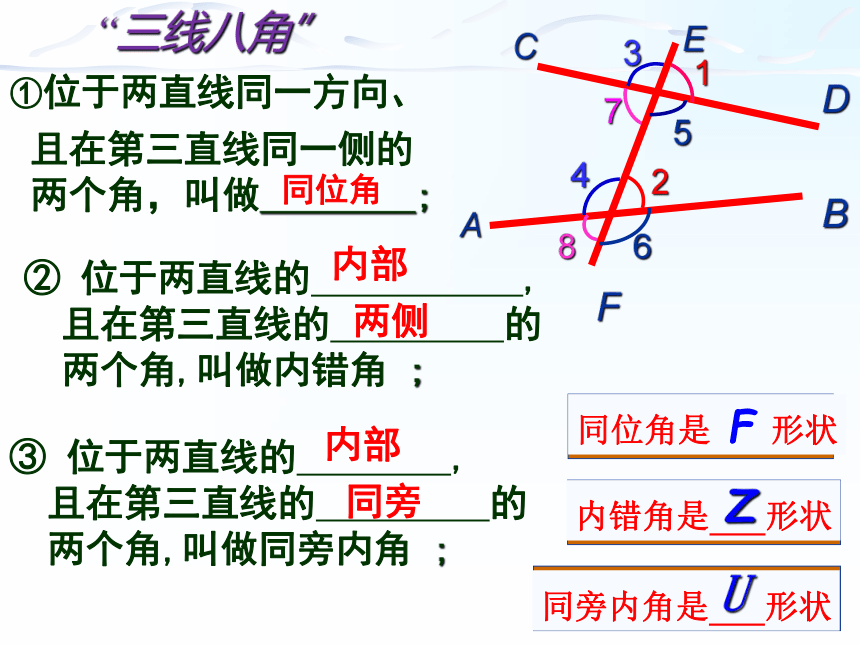
“三线八角”
F
D
B
C
A
1
3
7
5
2
8
6
E
4
①位于两直线同一方向、
② 位于两直线的 ,
且在第三直线的 的
两个角,叫做内错角 ;
且在第三直线同一侧的
两个角，叫做 ;
同位角
内部
两侧
③ 位于两直线的 ,
且在第三直线的 的
两个角,叫做同旁内角 ;
内部
同旁
同位角是 F 形状
内错角是 形状
Z
同旁内角是 形状
U
复习引入：
(1)∵ ∠1____∠2 (已知)
∴ a ∥ b ( )
(2)∵ ∠2____∠3 (已知)
∴ a ∥ b ( )
(3)∵ ∠2＋∠4=____(已知)，
∴ a ∥ b ( )
=
同位角相等，两直线平行
=
内错角相等，两直线平行
180°
同旁内角互补，两直线平行
同位角相等，两直线平行.
内错角相等，两直线平行.
同旁内角互补，两直线平行.
平行线的判定
两直线平行，同位角相等.
两直线平行，内错角相等.
两直线平行，同旁内角互补.
？
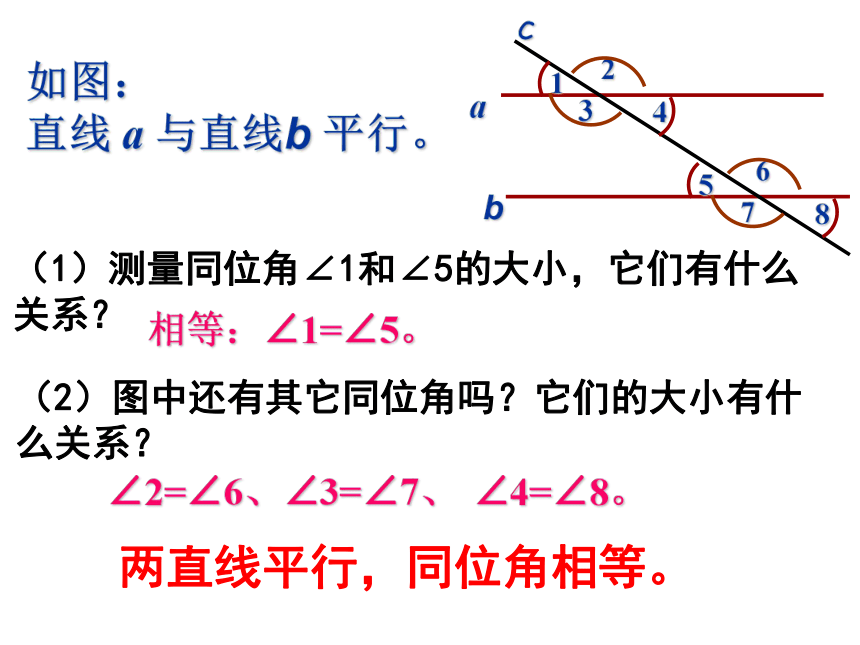
如图：
直线 a 与直线b 平行。
（1）测量同位角∠1和∠5的大小，它们有什么关系？
相等：∠1=∠5。
∠2=∠6、
∠3=∠7、
∠4=∠8。
b
a
c
8
3
2
1
4
6
7
5
两直线平行，同位角相等。
（2）图中还有其它同位角吗？它们的大小有什
么关系？
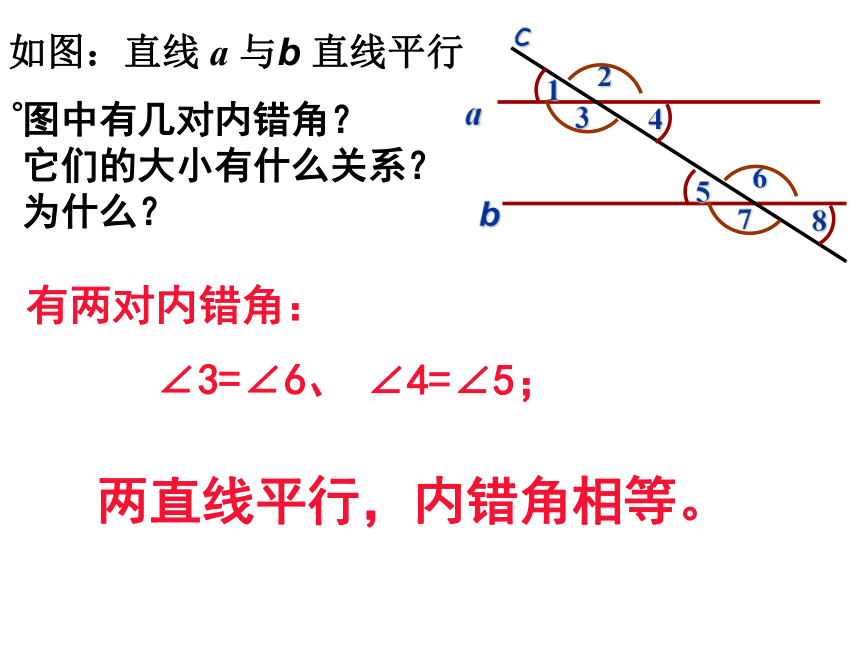
如图：直线 a 与b 直线平行。
图中有几对内错角？
它们的大小有什么关系？
为什么？
有两对内错角：
∠3=∠6、
∠4=∠5；
两直线平行，内错角相等。
b
a
c
8
3
2
1
4
6
7
5
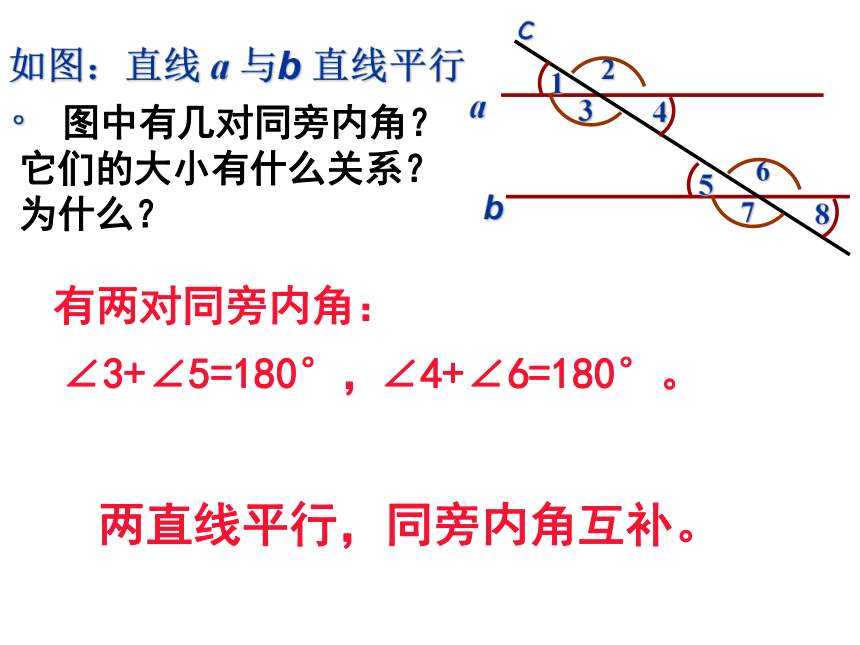
如图：直线 a 与b 直线平行。
有两对同旁内角：
∠3+∠5=180°，
∠4+∠6=180°。
两直线平行，同旁内角互补。
b
a
c
8
3
2
1
4
6
7
5
图中有几对同旁内角？
它们的大小有什么关系？
为什么？
简记为：
两条平行直线被第三条直线直线所截，
两直线平行，内错角相等。
两直线平行，同旁内角互补
两直线平行，同位角相等。
平行直线的特征
（性质）
同位角相等，内错角相等，同旁内角互补。
两类定理的比较
两条平行直线被第三条直线直线所截，
思考:
1、判定定理与性质定理的
条件与结论有什么关系？
互换。
2、使用判定定理时是
已知 ，说明 ；
角的相等或互补
二直线平行
使用性质定理时是
已知 ，说明 。
二直线平行
角的相等或互补
判定定理（平行条件） 性质定理（平行特征）
条件 结论 条件 结论
同位角相等　 两直线平行
两直线平行 同位角相等
内错角相等　 两直线平行
两直线平行 内错角相等
同旁内角互补　两直线平行
两直线平行 同旁内角互补
A
B
C
D
1
填空:
如图:
①∵AD//BC
∴∠B=∠1 ( )
②∵AB//CD
∴∠D＝∠1 ( )
③∵AD//BC
∴∠C＋____＝180
( )
两直线平行，同位角相等
两直线平行，同旁内角互补
两直线平行，内错角相等
∠D
如图：AB,CD被EF所截，AB∥CD。
若∠1＝120° 则∠2＝ ＿＿
（ 　　　）
∠3＝ ＿＿ －∠1＝＿＿＿
（ 　　　 ）
60°
A
B
C
D
E
F
1
2
3
练一练
120 °
两直线平行，内错角相等
180°
两直线平行，同旁内角互补
做一做
如图：一束平行光线AB和DE射向一个水平镜面后被反射，
（1）∠1，∠3的大小有什么关系？
∠2与∠4呢？
∵AB∥DE （已知）
∴∠1=∠3
(两直线平行，同位角相等)
相等：∠1=∠3；
（2 ）反射光线BC与EF也平行吗？
∵ ∠2=∠4
∴ BC∥EF
平行：
∵ ∠1=∠2 ，∠3=∠4
∴ ∠2=∠4 （等量代换）
A
B
D
E
C
F
此时∠1=∠2 ， ∠3=∠4 。
1
3
2
4
∠2 =∠4 。
B
E
随堂练习
1、如图所示，AB∥CD，AC∥BD。
分别找出与∠1相等或互补的角。
如图，与∠1相等的角有：
与∠1互补的角有：
1
A
B
D
C
7个
8个
随堂练习
p 60
1、如图所示，AB∥CD，AC∥BD。
分别找出与∠1相等或互补的角。
如图，与∠1相等的角有：
∠3， ∠5， ∠7， ∠9，
∠11， ∠13， ∠15；
与∠1互补的角有：
∠2， ∠4， ∠6， ∠8，
∠10， ∠12， ∠14， ∠16 ；
解:
1
14
16
13
15
3
A
B
D
C
2
4
5
6
7
8
9
10
12
11
1. 平行线的特征：
两直线平行，同位角相等；
两直线平行，内错角相等；
两直线平行，同旁内角互补。
2. 注意：特征与判定的区别
两类定理的比较
两条直线被第三条直线所截
同位角相等， 两直线平行
两直线平行，同位角相等。
平行线的判定
平行线的特征
条件 结论
条件 结论
内错角相等， 两直线平行
两直线平行，内错角相等。
同旁内角互补，两直线平行
两直线平行，同旁内角互补
作业：
1 、课本P62 习题 2.4
2 、带圆规和三角板
c
d
a
b
3
4
2
1
例2 如图所示 ∠1 =∠2
求证 ： ∠3 =∠4
证明：∵ ∠1 =∠2（已知）
∴a//b
(同位角相等,两直线平行)
∴ ∠3 =∠4
(两直线平行，内错角相等)
4.如图a∥b，c ∥d，∠１=60°,
那么 ①∠2=____
②∠3=____
③ ∠4=____
④ ∠5=____
120°
60°
60°
60°
a
2
b
60°
d
1
5
3
4
c
A
B
C
D
115°
110°
　　如图，是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片，工作人员从玉片上已经量得A=115°，∠D=100°。已知梯形的两底AD//BC，请你求出另外两个角的度数
解:
∵ AD//BC(已知)
∴ A+ B =180°
（两直线平行，同旁内角互补）
∴ B =180°－ A
　　 =180°－ 115°
=65 °
同理： C =180°－ D =180°－ 110° =70 °
例1：如图，已知AG//CF，AB//CD，
∠A＝40 ，求∠C的度数。
F
A
B
C
D
E
G
1
解:
∵ AG//CF(已知)
∴ ∠A=∠1
(两直线平行,同位角相等)
∵AB//CD(已知)
∴ ∠1=∠C
(两直线平行,同位角相等)
∴ ∠A=∠C
(等量代换)
∵ ∠A＝40
∴ ∠C＝40
1、如图、已知 1=60°、 2=60°
3=78°、求 4.
B
3
4
1
2
A
C
D
解: ∵ 1=60°, 2=60°
∴ 3+ 4=180°（两直线平行，同旁内角互补）
∴ 4=180°- 78°=102°
∴AB//CD（内错角相等，两直线平行）
练一练：
∴ 1= 2
练一练：
2、如图，⑴如果AB//PC，∠P =35°，那么∠PAB=_____；
145°
58°
3
180°
⑵如果AD//BC，∠2=18°，
∠5=40°，那么ABC=_____；
⑶如果AP//BD，那么∠P=∠___；
⑷如果AB//CD，那么∠ABC+ ∠C =____.
C
B
A
D
P
4
5
2
3
1
议一议 ：
如图，直线AB//CD，E在AB与CD之间，
且∠B=61°，∠D=34°.
求∠BED的度数.
A
B
E
D
C
1
2
两直线平行
同位角相等
内错角相等
同旁内角互补
同位角相等
内错角相等
同旁内角互补
两直线平行
平行特征
平行条件