西师大版数学五年级上册5.4 梯形的面积(1)课件(24张ppt)
文档属性
| 名称 | 西师大版数学五年级上册5.4 梯形的面积(1)课件(24张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-09 18:49:21 | ||
图片预览






文档简介
西师版数学五年级(上)
第4课时 梯形的面积(1)
多边形面积的计算
5
1. 经历梯形的面积计算公式的推导过程。
2. 会正确、熟练地运用公式计算梯形的面积,并能解决一些生活中的实际问题。
3. 通过自主探究,小组合作,在操作、观察、比较中,培养想象力、思考力,发展自身的空间观念。
4. 渗透数学迁移、转化思想,感受数学与生活的紧密联系,提高学习数学的兴趣。
学习目标
【重点】
理解并掌握梯形的面积计算公式,
会计算梯形的面积。
【难点】
理解梯形面积计算公式的推导过程。
课堂导入
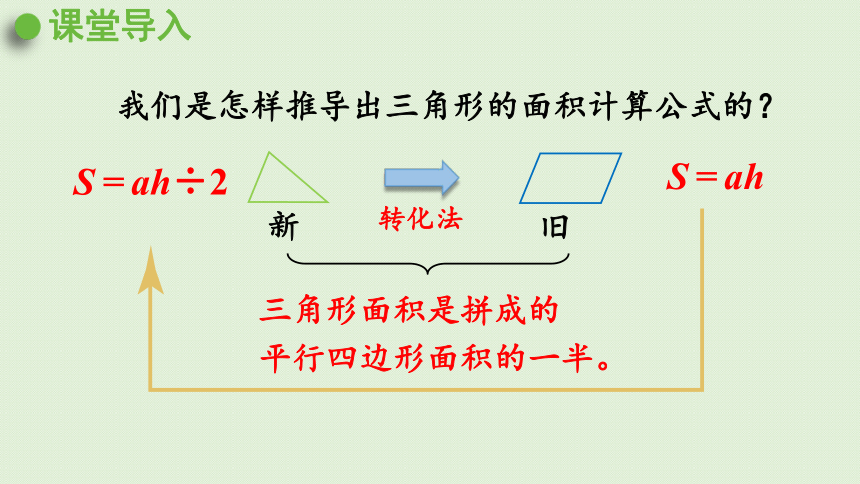
转化法
三角形面积是拼成的
平行四边形面积的一半。
S=ah
S=ah÷2
旧
新
我们是怎样推导出三角形的面积计算公式的?
新知探究
1
用梯形学具探讨梯形面积计算公式。
我想把梯形转化成平行四边形。
我想用剪的方法……
我用两个相同的梯形拼成……
同学们各抒己见,分小组讨论一下这个问题吧!
(教材第85页例1)
小组合作:梯形的面积怎么算?
合作要求
1.剪一剪,拼一拼,看看能把梯形转化成你学过的什么图形?
2.组内交流,说说自己的推导方法。
3.归纳小结,准备全班汇报。
高
下底
上底
高
下底
上底
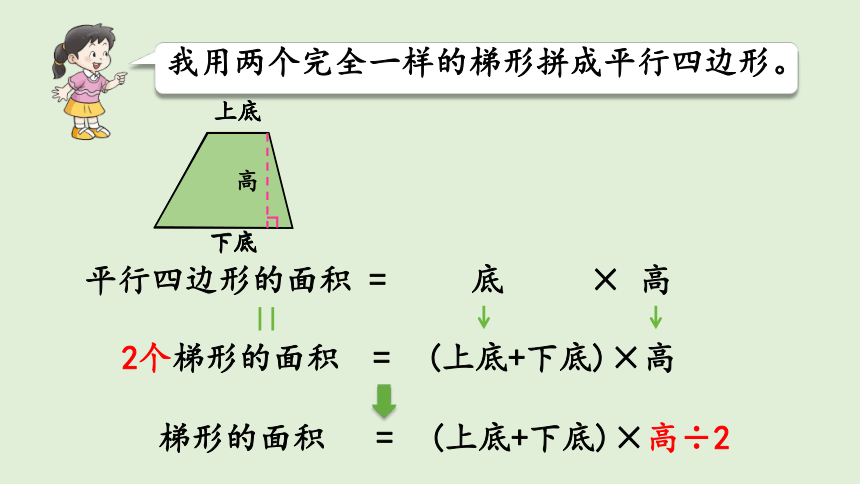
平行四边形的面积 = 底 × 高
2个梯形的面积 = (上底+下底)×高
梯形的面积 = (上底+下底)×高÷2
我用两个完全一样的梯形拼成平行四边形。
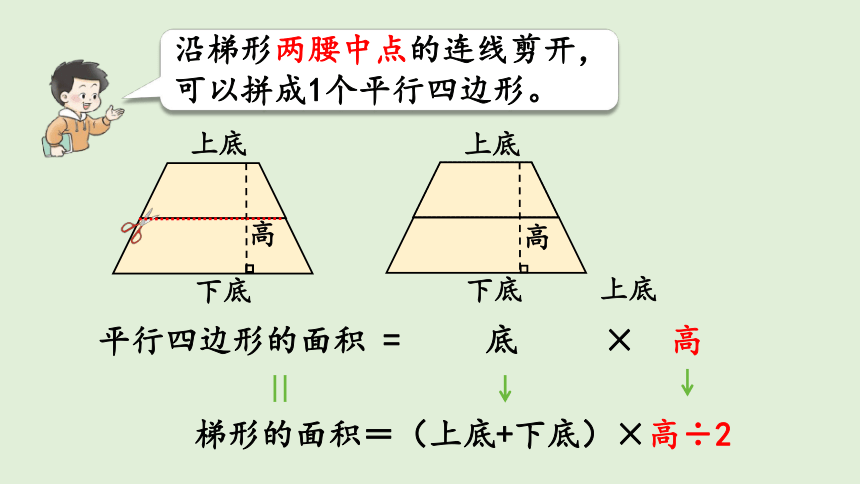
沿梯形两腰中点的连线剪开,可以拼成1个平行四边形。
上底
下底
高
上底
下底
高
上底
平行四边形的面积 = 底 × 高
梯形的面积=(上底+下底)×高÷2
高
下底
上底
高
梯形的面积 = 左边三角形面积 + 右边三角形面积
= 上底×高÷2 + 下底×高÷2
= (上底+下底)×高÷2
把梯形剪成两个三角形。
高
下底
上底
高
梯形的面积 = 平行四边形面积 + 三角形面积
= 上底×高 + (下底-上底)×高÷2
= (上底+下底)×高÷2
上底
把梯形剪成一个三角形和一个平行四边形。
每个梯形的面积等于拼成的平行四边形面积的一半。
(上底+下底)×高÷2
梯形的面积 = 平行四边面积的一半
=
高
下底
上底
下底
上底
这个平行四边形的底等于梯形的上下底之和,高等于梯形的高。
两个完全一样的梯形可以拼成一个平行四边形。
观察拼成的平行四边形和原来的梯形,你发现了什么?
如果用 S 表示梯形的面积,用 a、b 和 h 分别
表示梯形的上底、下底和高,那么梯形的面积
计算公式是:
????
?
????
?
S = (a+b)h÷2
????
?
5 cm
3 cm
答:这个梯形的面积是10.5 cm?。
一个梯形的上底是2 cm,下底是5 cm,高是3 cm。求这个梯形的面积。
试一试
2 cm
梯形的面积=(上底+下底)×高÷2
=(2+5)×3÷2
=7×3÷2
=10.5 (cm?)
(教材第86页试一试)
课
堂
活
动
画一画,算一算。
在每个方格是1平方厘米的方格纸上画一个梯形,并算出它的面积。
(3+7)×3÷2=15(cm?)
(教材第86页课堂活动第1题)
课堂练习
1.计算下面梯形的面积。
(教材第86页练习二十一第1题)
2 cm
4 cm
3 cm
6.4 dm
5 dm
3.2 dm
9.2 cm
5.5 cm
4 cm
(2+4)×3÷2
=9(cm?)
(3.2+6.4)×5÷2
=24(dm?)
(4+9.2)×5.5÷2
=36.3(cm?)
2.先量出下图中有关数据,再计算图形面积。
(教材第86页练习二十一第2题)
(测量过程请在课本上完成)
3.
6 cm
12 cm
30 cm
这个航模机翼的面积是多少平方厘米?
(6+12)×30÷2×2
= 540(cm?)
答:这个航模机翼的面积是540 cm?。
(教材第86页练习二十一第3题)
两块玻璃都是梯形,分别将上、下底和高的值代入公式计算,即可求解。
注意:结果单位不要丢掉。
4.一辆汽车侧面的两块玻璃的形状是梯形(如下图),它们的面积分别是多少?
40 cm
45 cm
71 cm
65 cm
40 cm
S =(a + b)h÷2
=(40 + 71)×40÷2
= 111×40÷2
= 2220(cm2)
S =(a + b)h÷2
=(45 + 65)×40÷2
= 110×40÷2
= 2200(cm2)
答:它们的面积分别是 2220 cm2和2200 cm2。
40 cm
45 cm
71 cm
65 cm
40 cm
这个算式符合梯形面积计算公式的特点,所以这个图形是梯形,且上、下底和高对应的长度依次是6 cm、4 cm和3 cm。
5.下图中每个小正方形的边长都是1 cm,请你根据图形面积的算式(6+4)×3÷2,画出相应的图形。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
(画法不唯一)
6. 2020年某地新建一个综合性公园。一条景观河穿过如图所示的这块地,工程队计划将这块地铺上草皮,请算出铺草皮的面积。
左三角形的面积:40×50÷2=1000(m?)
右三角形的面积:80×50÷2=2000(m?)
铺草皮的面积:1000+2000=3000(m?)
80 m
40 m
10 m
50 m
看图可知:铺草皮的面积=左三角形的面积+右三角形的面积
答:铺草皮的面积是3000 m?。
6.2020年某地新建一个综合性公园。一条景观河穿过如图所示的这块地,工程队计划将这块地铺上草皮,请算出铺草皮的面积。
(40+80)×50÷2=3000(m?)
80 m
40 m
10 m
50 m
假如去掉景观河,将地的两部分拼在一起,就是一个上底40 m、下底80 m、高50 m的梯形。
答:铺草皮的面积是3000 m?。
课堂小结
我们通过剪一剪、拼一拼推导出梯形面积公式:梯形的面积=(上底+下底)×高÷2,用字母表示为S=(a+b)h÷2。
在利用S=(a+b)h÷2求面积时,要注意书写格式,计算结果还要写上单位名称。
这节课你有什么收获?
02
01
课后作业
练习二十一第1、2、3题。
作业课件中的相关练习。
第4课时 梯形的面积(1)
多边形面积的计算
5
1. 经历梯形的面积计算公式的推导过程。
2. 会正确、熟练地运用公式计算梯形的面积,并能解决一些生活中的实际问题。
3. 通过自主探究,小组合作,在操作、观察、比较中,培养想象力、思考力,发展自身的空间观念。
4. 渗透数学迁移、转化思想,感受数学与生活的紧密联系,提高学习数学的兴趣。
学习目标
【重点】
理解并掌握梯形的面积计算公式,
会计算梯形的面积。
【难点】
理解梯形面积计算公式的推导过程。
课堂导入
转化法
三角形面积是拼成的
平行四边形面积的一半。
S=ah
S=ah÷2
旧
新
我们是怎样推导出三角形的面积计算公式的?
新知探究
1
用梯形学具探讨梯形面积计算公式。
我想把梯形转化成平行四边形。
我想用剪的方法……
我用两个相同的梯形拼成……
同学们各抒己见,分小组讨论一下这个问题吧!
(教材第85页例1)
小组合作:梯形的面积怎么算?
合作要求
1.剪一剪,拼一拼,看看能把梯形转化成你学过的什么图形?
2.组内交流,说说自己的推导方法。
3.归纳小结,准备全班汇报。
高
下底
上底
高
下底
上底
平行四边形的面积 = 底 × 高
2个梯形的面积 = (上底+下底)×高
梯形的面积 = (上底+下底)×高÷2
我用两个完全一样的梯形拼成平行四边形。
沿梯形两腰中点的连线剪开,可以拼成1个平行四边形。
上底
下底
高
上底
下底
高
上底
平行四边形的面积 = 底 × 高
梯形的面积=(上底+下底)×高÷2
高
下底
上底
高
梯形的面积 = 左边三角形面积 + 右边三角形面积
= 上底×高÷2 + 下底×高÷2
= (上底+下底)×高÷2
把梯形剪成两个三角形。
高
下底
上底
高
梯形的面积 = 平行四边形面积 + 三角形面积
= 上底×高 + (下底-上底)×高÷2
= (上底+下底)×高÷2
上底
把梯形剪成一个三角形和一个平行四边形。
每个梯形的面积等于拼成的平行四边形面积的一半。
(上底+下底)×高÷2
梯形的面积 = 平行四边面积的一半
=
高
下底
上底
下底
上底
这个平行四边形的底等于梯形的上下底之和,高等于梯形的高。
两个完全一样的梯形可以拼成一个平行四边形。
观察拼成的平行四边形和原来的梯形,你发现了什么?
如果用 S 表示梯形的面积,用 a、b 和 h 分别
表示梯形的上底、下底和高,那么梯形的面积
计算公式是:
????
?
????
?
S = (a+b)h÷2
????
?
5 cm
3 cm
答:这个梯形的面积是10.5 cm?。
一个梯形的上底是2 cm,下底是5 cm,高是3 cm。求这个梯形的面积。
试一试
2 cm
梯形的面积=(上底+下底)×高÷2
=(2+5)×3÷2
=7×3÷2
=10.5 (cm?)
(教材第86页试一试)
课
堂
活
动
画一画,算一算。
在每个方格是1平方厘米的方格纸上画一个梯形,并算出它的面积。
(3+7)×3÷2=15(cm?)
(教材第86页课堂活动第1题)
课堂练习
1.计算下面梯形的面积。
(教材第86页练习二十一第1题)
2 cm
4 cm
3 cm
6.4 dm
5 dm
3.2 dm
9.2 cm
5.5 cm
4 cm
(2+4)×3÷2
=9(cm?)
(3.2+6.4)×5÷2
=24(dm?)
(4+9.2)×5.5÷2
=36.3(cm?)
2.先量出下图中有关数据,再计算图形面积。
(教材第86页练习二十一第2题)
(测量过程请在课本上完成)
3.
6 cm
12 cm
30 cm
这个航模机翼的面积是多少平方厘米?
(6+12)×30÷2×2
= 540(cm?)
答:这个航模机翼的面积是540 cm?。
(教材第86页练习二十一第3题)
两块玻璃都是梯形,分别将上、下底和高的值代入公式计算,即可求解。
注意:结果单位不要丢掉。
4.一辆汽车侧面的两块玻璃的形状是梯形(如下图),它们的面积分别是多少?
40 cm
45 cm
71 cm
65 cm
40 cm
S =(a + b)h÷2
=(40 + 71)×40÷2
= 111×40÷2
= 2220(cm2)
S =(a + b)h÷2
=(45 + 65)×40÷2
= 110×40÷2
= 2200(cm2)
答:它们的面积分别是 2220 cm2和2200 cm2。
40 cm
45 cm
71 cm
65 cm
40 cm
这个算式符合梯形面积计算公式的特点,所以这个图形是梯形,且上、下底和高对应的长度依次是6 cm、4 cm和3 cm。
5.下图中每个小正方形的边长都是1 cm,请你根据图形面积的算式(6+4)×3÷2,画出相应的图形。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
(画法不唯一)
6. 2020年某地新建一个综合性公园。一条景观河穿过如图所示的这块地,工程队计划将这块地铺上草皮,请算出铺草皮的面积。
左三角形的面积:40×50÷2=1000(m?)
右三角形的面积:80×50÷2=2000(m?)
铺草皮的面积:1000+2000=3000(m?)
80 m
40 m
10 m
50 m
看图可知:铺草皮的面积=左三角形的面积+右三角形的面积
答:铺草皮的面积是3000 m?。
6.2020年某地新建一个综合性公园。一条景观河穿过如图所示的这块地,工程队计划将这块地铺上草皮,请算出铺草皮的面积。
(40+80)×50÷2=3000(m?)
80 m
40 m
10 m
50 m
假如去掉景观河,将地的两部分拼在一起,就是一个上底40 m、下底80 m、高50 m的梯形。
答:铺草皮的面积是3000 m?。
课堂小结
我们通过剪一剪、拼一拼推导出梯形面积公式:梯形的面积=(上底+下底)×高÷2,用字母表示为S=(a+b)h÷2。
在利用S=(a+b)h÷2求面积时,要注意书写格式,计算结果还要写上单位名称。
这节课你有什么收获?
02
01
课后作业
练习二十一第1、2、3题。
作业课件中的相关练习。
