西师大版数学五年级上册5.6 不规则图形的面积 课件 (21张PPT)
文档属性
| 名称 | 西师大版数学五年级上册5.6 不规则图形的面积 课件 (21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-09 16:00:31 | ||
图片预览



文档简介
西师版数学五年级(上)
第6课时 不规则图形的面积
多边形面积的计算
5
1. 通过交流估算面积的方法,培养合作意识,借助操作等实践活动自主解决问题。
2. 在估计不规则图形面积的过程中,培养空间观念以及估算意识和能力。
3. 学习用数方格的方法计算不规则图形的面积,能估算不规则图形的面积大小,并能用不同方法灵活估算面积。
学习目标
【重点】
掌握用方格纸和参照规则图形面积估算不规则图形面积的方法。
【难点】
能用不同方法灵活估算不规则图形的
面积。
长安村为了更好地搞好生产,新规划了几块地作为试验田,你能求出下图中试验田的面积吗?
课堂导入
像这种边缘有的地方凸出一些,有的地方凹进去一些的不是很规则的图形,我们叫它不规则图形。
新知探究
实验田大约有多大?
(教材第88页例题)
我们能准确算出不规则图形的面积吗?
我们还不能准确算出不规则图形的面积,但是可以估算出它的面积。
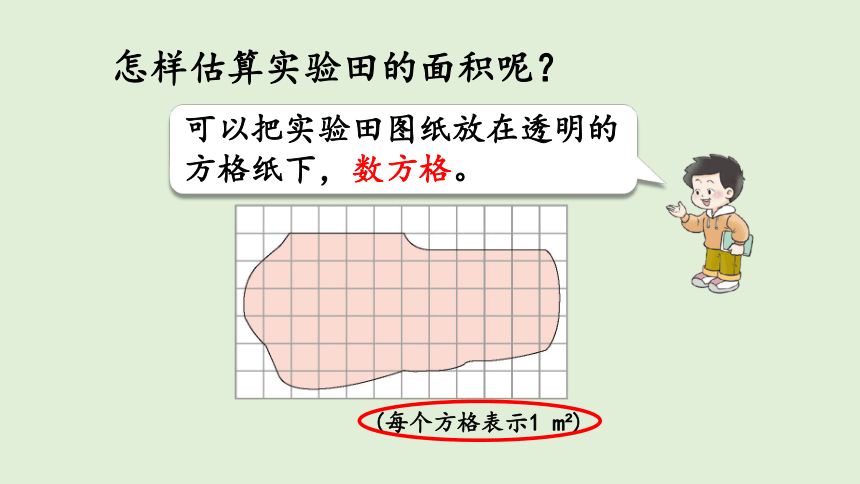
怎样估算实验田的面积呢?
可以把实验田图纸放在透明的方格纸下,数方格。。
(每个方格表示1 m?)
(每个方格表示1 m?)
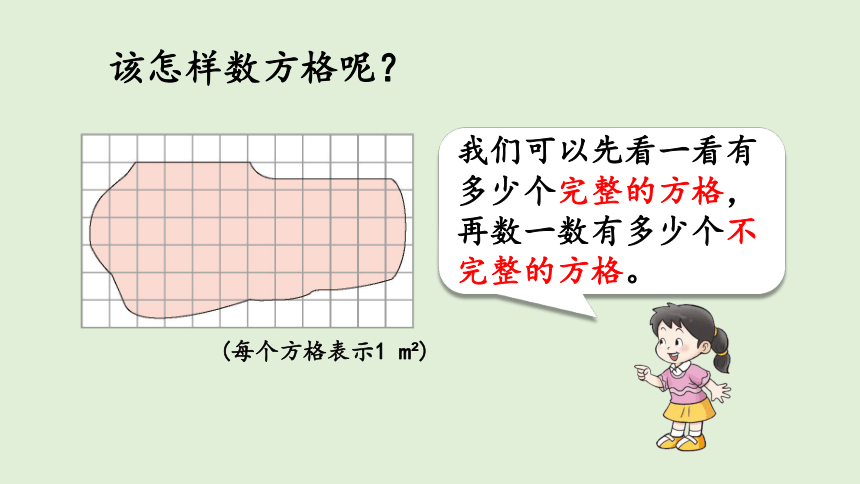
该怎样数方格呢?
我们可以先看一看有多少个完整的方格,再数一数有多少个不完整的方格。。
(每个方格表示1 m?)
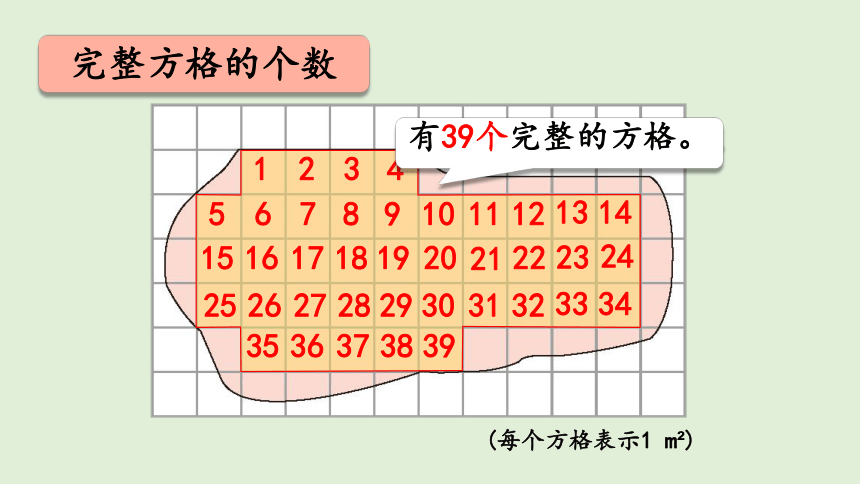
完整方格的个数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
有39个完整的方格。。
(每个方格表示1 m?)
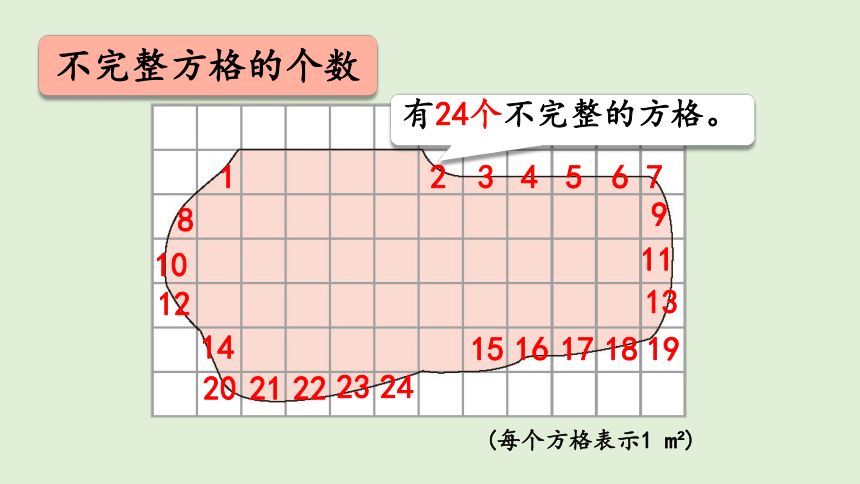
不完整方格的个数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
有24个不完整的方格。。
这块实验田的面积大约在什么范围?
如果只看整方格,有39个,比实际面积小。。
如果把不完整的方格都算作整方格,就共有63个,比实际面积大了。
试验田面积在39至63平方米之间。
一般情况下,不完整的方格看作半格。这里有24个不完整的方格,看作12个整方格。
39+12 = 51(m?)
答:实验田大约有51 m?。
估计下面残缺地砖的面积。(每个方格表示1 dm?。)
试一试
完整方格有3个
1
2
3
1
2
3
4
5
不完整方格有5个
3+5÷2=5.5(dm?)
1
2
完整方格有2个
1
2
3
4
不完整方格有4个
2+4÷2 =4(dm?)
1
2
3
4
5
6
7
1
2
3
4
5
完整方格有7个
不完整方格有5个
7+5÷2=9.5(dm?)
(教材第88页试一试)
同桌两个同学分别用剪刀剪出一些不规则的纸片,再用透明方格纸估测它们的面积。
数方格的方法:完整方格数+不完整方格数÷2
课
堂
活
动
(教材第89页课堂活动)
课堂练习
1.下面这块田的面积大约有多少平方米?
(每个方格表示1 m?。)
(教材第89页练习二十二第1题)
55+28÷2=69(m?)
答:这块田的面积大约有69 m?。
2.下面两个小岛,谁的面积大?
(教材第89页练习二十二第2题)
28+22÷2=39
35+26÷2=48
两个图中方格大小相同,因此总方格数多的面积大。
(教材第89页练习二十二第2题)
大
3.有一块近似平行四边形的土地,底是43 m,高是20.1 m。这块地的面积约是多少平方米?(得数保留整数。)
43×20.1=864.3(m2)≈864(m2)
答:这块地的面积约是864 m2。
依题意,找出底和高的数值,直接代入平行四边形的面积计算公式即可求解。
4.图中每个小方格的面积为1 cm?,计算涂色部分的面积。
涂色部分可分成一个三角形和一个梯形,找出相应的数值,就可代入三角形和梯形的面积公式进行计算。
三角形: 5×4÷2 =10(cm2)
梯 形:(5+2)×4÷2 =14(cm2)
涂色部分:10+14 = 24(cm2)
答:涂色部分的面积是24 cm2。
5.图中每个小方格的面积为1 m2,请你估算这个池塘的面积。
本题可以通过数方格,也可以转化为长方形来估算。
S = ab
= 12×8
= 96(m2)
答:这个池塘的面积
大约是96 m2。
课堂小结
估算不规则图形的面积,可以通过数方格的方法确定出不规则图形面积的范围,再估算出其面积的大小。
也可以将不规则图形的面积转化为与它形状相近的已学过的图形来估算。
这节课你有什么收获?
02
01
课后作业
练习二十二第1、2题。
作业课件中的相关练习。
第6课时 不规则图形的面积
多边形面积的计算
5
1. 通过交流估算面积的方法,培养合作意识,借助操作等实践活动自主解决问题。
2. 在估计不规则图形面积的过程中,培养空间观念以及估算意识和能力。
3. 学习用数方格的方法计算不规则图形的面积,能估算不规则图形的面积大小,并能用不同方法灵活估算面积。
学习目标
【重点】
掌握用方格纸和参照规则图形面积估算不规则图形面积的方法。
【难点】
能用不同方法灵活估算不规则图形的
面积。
长安村为了更好地搞好生产,新规划了几块地作为试验田,你能求出下图中试验田的面积吗?
课堂导入
像这种边缘有的地方凸出一些,有的地方凹进去一些的不是很规则的图形,我们叫它不规则图形。
新知探究
实验田大约有多大?
(教材第88页例题)
我们能准确算出不规则图形的面积吗?
我们还不能准确算出不规则图形的面积,但是可以估算出它的面积。
怎样估算实验田的面积呢?
可以把实验田图纸放在透明的方格纸下,数方格。。
(每个方格表示1 m?)
(每个方格表示1 m?)
该怎样数方格呢?
我们可以先看一看有多少个完整的方格,再数一数有多少个不完整的方格。。
(每个方格表示1 m?)
完整方格的个数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
有39个完整的方格。。
(每个方格表示1 m?)
不完整方格的个数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
有24个不完整的方格。。
这块实验田的面积大约在什么范围?
如果只看整方格,有39个,比实际面积小。。
如果把不完整的方格都算作整方格,就共有63个,比实际面积大了。
试验田面积在39至63平方米之间。
一般情况下,不完整的方格看作半格。这里有24个不完整的方格,看作12个整方格。
39+12 = 51(m?)
答:实验田大约有51 m?。
估计下面残缺地砖的面积。(每个方格表示1 dm?。)
试一试
完整方格有3个
1
2
3
1
2
3
4
5
不完整方格有5个
3+5÷2=5.5(dm?)
1
2
完整方格有2个
1
2
3
4
不完整方格有4个
2+4÷2 =4(dm?)
1
2
3
4
5
6
7
1
2
3
4
5
完整方格有7个
不完整方格有5个
7+5÷2=9.5(dm?)
(教材第88页试一试)
同桌两个同学分别用剪刀剪出一些不规则的纸片,再用透明方格纸估测它们的面积。
数方格的方法:完整方格数+不完整方格数÷2
课
堂
活
动
(教材第89页课堂活动)
课堂练习
1.下面这块田的面积大约有多少平方米?
(每个方格表示1 m?。)
(教材第89页练习二十二第1题)
55+28÷2=69(m?)
答:这块田的面积大约有69 m?。
2.下面两个小岛,谁的面积大?
(教材第89页练习二十二第2题)
28+22÷2=39
35+26÷2=48
两个图中方格大小相同,因此总方格数多的面积大。
(教材第89页练习二十二第2题)
大
3.有一块近似平行四边形的土地,底是43 m,高是20.1 m。这块地的面积约是多少平方米?(得数保留整数。)
43×20.1=864.3(m2)≈864(m2)
答:这块地的面积约是864 m2。
依题意,找出底和高的数值,直接代入平行四边形的面积计算公式即可求解。
4.图中每个小方格的面积为1 cm?,计算涂色部分的面积。
涂色部分可分成一个三角形和一个梯形,找出相应的数值,就可代入三角形和梯形的面积公式进行计算。
三角形: 5×4÷2 =10(cm2)
梯 形:(5+2)×4÷2 =14(cm2)
涂色部分:10+14 = 24(cm2)
答:涂色部分的面积是24 cm2。
5.图中每个小方格的面积为1 m2,请你估算这个池塘的面积。
本题可以通过数方格,也可以转化为长方形来估算。
S = ab
= 12×8
= 96(m2)
答:这个池塘的面积
大约是96 m2。
课堂小结
估算不规则图形的面积,可以通过数方格的方法确定出不规则图形面积的范围,再估算出其面积的大小。
也可以将不规则图形的面积转化为与它形状相近的已学过的图形来估算。
这节课你有什么收获?
02
01
课后作业
练习二十二第1、2题。
作业课件中的相关练习。
