西师大版数学五年级上册5.11 多边形面积的计算 整理与复习 课件(21张)
文档属性
| 名称 | 西师大版数学五年级上册5.11 多边形面积的计算 整理与复习 课件(21张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-19 14:13:47 | ||
图片预览




文档简介
西师版数学五年级(上)
第11课时 整理与复习
多边形面积的计算
5
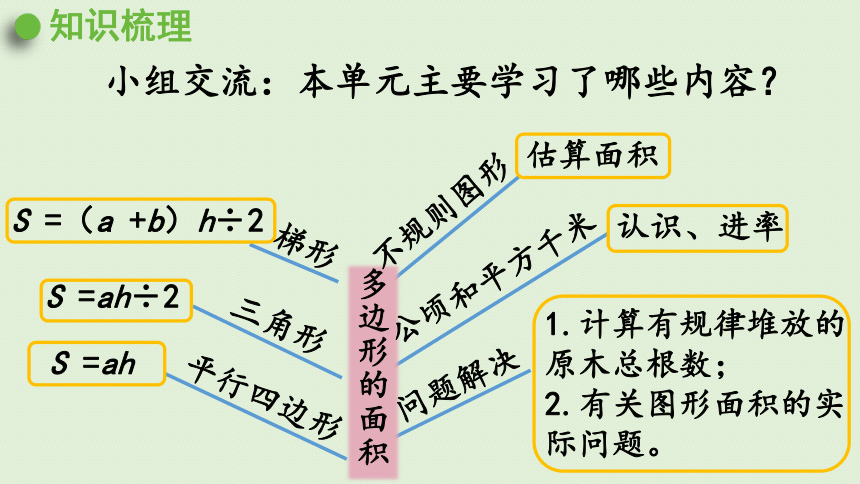
小组交流:本单元主要学习了哪些内容?
知识梳理
多边形的面积
平行四边形
三角形
梯形
不规则图形
公顷和平方千米
问题解决
S =ah
S =ah÷2
S =(a +b)h÷2
估算面积
认识、进率
1.计算有规律堆放的原木总根数;
2.有关图形面积的实际问题。
要点回顾
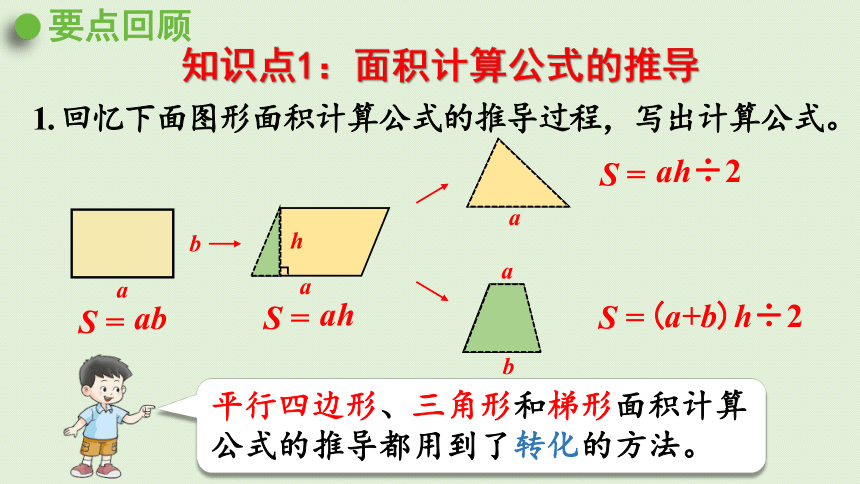
1. 回忆下面图形面积计算公式的推导过程,写出计算公式。
平行四边形、三角形和梯形面积计算公式的推导都用到了转化的方法。
a
b
S =
ab
a
h
S =
ah
a
h
S =
ah÷2
b
h
a
S =
(a+b)h÷2
知识点1:面积计算公式的推导
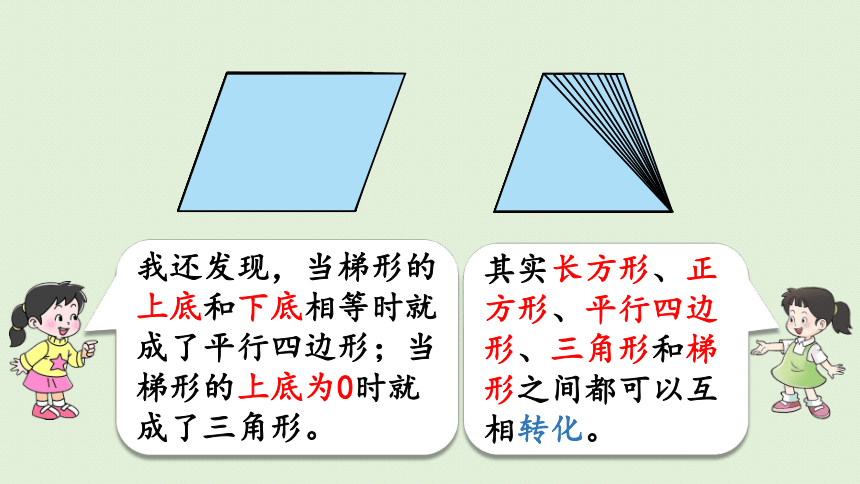
我还发现,当梯形的上底和下底相等时就成了平行四边形;当梯形的上底为0时就成了三角形。
其实长方形、正方形、平行四边形、三角形和梯形之间都可以互相转化。
知识点2:面积的计算
2.计算下面图形的面积。
利用字母公式进行计算,先要找到相应的数值,再代入公式计算,最后还要加上单位。
S=ah
=270(cm2)
=18×15
S=ah÷2
=96(cm2)
=24×8÷2
S=a2
=3.61(m2)
=1.9×1.9
15 cm
18 cm
8 cm
24 cm
1.9 m
1.9 m
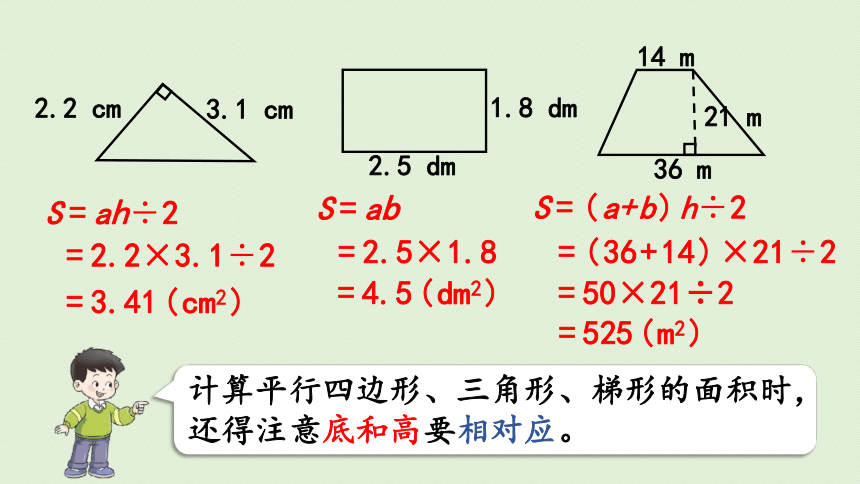
计算平行四边形、三角形、梯形的面积时,还得注意底和高要相对应。
S=ah÷2
=3.41(cm2)
=2.2×3.1÷2
S=ab
=4.5(dm2)
=2.5×1.8
S=(a+b)h÷2
=525(m2)
=(36+14)×21÷2
=50×21÷2
3.1 cm
2.2 cm
2.5 dm
1.8 dm
14 m
36 m
21 m
3. (1)两个完全相同的平行四边形(如下图),将图1和图2中涂色部分的面积比较,( ) 。
两幅图的涂色部分都是三角形,都和平行四边形等底等高,面积都是平行四边形的一半。
A. 图1面积大
B. 图2面积大
D. 无法比较
C. 图1和图2面积一样大
底
高
底
高
C
知识点3:图形间的关系
图1
图2
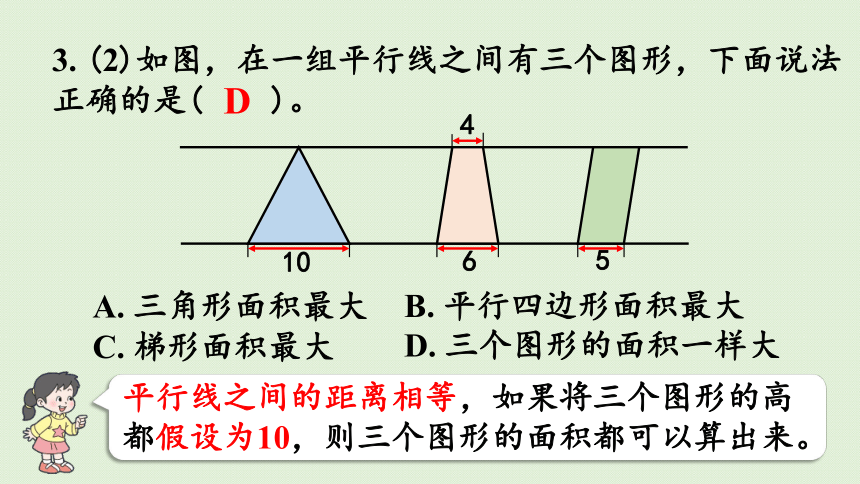
3. (2)如图,在一组平行线之间有三个图形,下面说法正确的是( )。
平行线之间的距离相等,如果将三个图形的高都假设为10,则三个图形的面积都可以算出来。
A. 三角形面积最大
B. 平行四边形面积最大
D. 三个图形的面积一样大
C. 梯形面积最大
10
5
6
4
D
图形间的面积比较,往往牵涉到图形间的关系:如三角形的面积是与它等底等高的平行四边形面积的一半等。
我们还经常用到如下这些规律:
等底等高的平行四边形面积相等;
等底等高的三角形面积相等;
面积相等的平行四边形、三角形或梯形,形状不一定相同等。
知识点4:不规则图形面积的估算
4. 图中每个小方格的面积是1 cm?,涂色部分的面积约是多少平方厘米?
不规则图形面积的估算有两种方法:①数方格;
②转化为简单图形估算。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
方法① :数方格
S=28+28÷2
=42(cm2)
答:涂色部分的面积约是42 cm2。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
方法② :转化成三角形
S三角形=ah÷2
=10×8÷2
=40(cm2)
答:涂色部分的面积约是
40 cm? 。
4. 图中每个小方格的面积是1 cm?,涂色部分的面积约是多少平方厘米?
知识点5:认识平方千米与公顷
5.在( )里填上合适的数。
0.5 hm?=( )m? 0.0068 km?=( )m?
900 m?=( )hm?
70 hm?=( )km?
5000
6800
0.09
0.7
要牢记1 hm2=10000 m2 、
1 km2=1000000 m2 、1 km2=100 hm2 。
知识点6:计算有规律堆放原木总根数
(顶层根数+底层根数)×层数÷2
我们经常见到像这样堆放的圆木、钢管,通常用下面算法求总根数:
层数:20-2+1=19(层)
总根数:(2+20)×19÷2=209(根)
答:这堆木料一共有209根。
6.家具厂有一堆木料堆放如下图,已知最上面一层有2根木料,最下面一层有20根木料,上面一层总比下面一层
少1根,这堆木料一共有多少根?
我知道,此类题可以根据公式(顶层根数+底层根数)×层数÷2进行计算。
(1)平行四边形的面积一定比梯形的面积大 ( )
(2)平行四边形的面积等于三角形面积的2倍。 ( )
(3)梯形的上底、下底越长,面积越大。 ( )
(4)任何一个梯形都可以分成两个等高的三角形。( )
(5)两个面积相等的三角形,一定能拼成一个平行
四边形。 ( )
课堂练习
1. 判断下面各题的叙述是否正确。
√
×
×
×
×
2.新华村开垦了一块近似于平行四边形的荒地 (如图所示),如果每公顷能收9300 kg玉米,
这块地大约能收多少千克玉米?
(教材第96页练习二十五第5题)
荒地面积为:
140×350=49000(m?)=4.9(hm?)
这块地能收玉米:
4.9×9300=45570(kg)
答:这块地大约能收45570 kg玉米。
3.这块钢板重多少千克?
每平方分米钢板重0.4千克。
梯形面积:(8+16)×14÷2=168(dm?)
梯形钢板重:168×0.4=67.2(kg)
答:这块钢板重67.2 kg。
8 dm
14 dm
16 dm
(教材第96页练习二十五第6题)
4.如图,是教室的一面墙的示意图。如果砌这面墙平均每平方米用砖 185 块,一共需要用多少块砖?
看图可知,这面墙由一个三角形和一个长方形组成。先求面积,再求出共需用砖的块数。
长方形面积:5×4 = 20(m2)
三角形面积:1.2×5÷2 = 3(m2)
墙的面积:20+3 = 23(m2)
砖的块数:185×23 = 4255(块)
答:一共需要4255块砖。
5.有一台收割机,作业宽度是1.8 m。每小时行5 km, 大约多长时间可以收割完下边这块地?
200 m
330 m
100 m
先求这块地的面积,再计算出收割机的工作效率,最后算工作时间。
5 km=5000 m
1.8×5000=9000(m2)
(200+330)×100÷2=26500(m2)
26500÷9000 ≈ 2.94(h)
答:大约2.94 h可以收割完这块地。
6.图中每个小方格的边长是1 m,请你估算涂色部分的面积。
S=S满格+S不满格
=26+42÷2
=47(m2)
=26+21
答:涂色部分的面积大约是47 m2 。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
本题可采用数方格的方法进行估算。
课堂小结
通过复习我还掌握不规则图形面积的计算方法。同时对平移、旋转等知识在公式推导过程中的应用理解更深了。
通过整理与复习,我掌握了平行四边形、三角形和梯形的面积计算公式的推导和运用。
这节课你有什么收获?
第11课时 整理与复习
多边形面积的计算
5
小组交流:本单元主要学习了哪些内容?
知识梳理
多边形的面积
平行四边形
三角形
梯形
不规则图形
公顷和平方千米
问题解决
S =ah
S =ah÷2
S =(a +b)h÷2
估算面积
认识、进率
1.计算有规律堆放的原木总根数;
2.有关图形面积的实际问题。
要点回顾
1. 回忆下面图形面积计算公式的推导过程,写出计算公式。
平行四边形、三角形和梯形面积计算公式的推导都用到了转化的方法。
a
b
S =
ab
a
h
S =
ah
a
h
S =
ah÷2
b
h
a
S =
(a+b)h÷2
知识点1:面积计算公式的推导
我还发现,当梯形的上底和下底相等时就成了平行四边形;当梯形的上底为0时就成了三角形。
其实长方形、正方形、平行四边形、三角形和梯形之间都可以互相转化。
知识点2:面积的计算
2.计算下面图形的面积。
利用字母公式进行计算,先要找到相应的数值,再代入公式计算,最后还要加上单位。
S=ah
=270(cm2)
=18×15
S=ah÷2
=96(cm2)
=24×8÷2
S=a2
=3.61(m2)
=1.9×1.9
15 cm
18 cm
8 cm
24 cm
1.9 m
1.9 m
计算平行四边形、三角形、梯形的面积时,还得注意底和高要相对应。
S=ah÷2
=3.41(cm2)
=2.2×3.1÷2
S=ab
=4.5(dm2)
=2.5×1.8
S=(a+b)h÷2
=525(m2)
=(36+14)×21÷2
=50×21÷2
3.1 cm
2.2 cm
2.5 dm
1.8 dm
14 m
36 m
21 m
3. (1)两个完全相同的平行四边形(如下图),将图1和图2中涂色部分的面积比较,( ) 。
两幅图的涂色部分都是三角形,都和平行四边形等底等高,面积都是平行四边形的一半。
A. 图1面积大
B. 图2面积大
D. 无法比较
C. 图1和图2面积一样大
底
高
底
高
C
知识点3:图形间的关系
图1
图2
3. (2)如图,在一组平行线之间有三个图形,下面说法正确的是( )。
平行线之间的距离相等,如果将三个图形的高都假设为10,则三个图形的面积都可以算出来。
A. 三角形面积最大
B. 平行四边形面积最大
D. 三个图形的面积一样大
C. 梯形面积最大
10
5
6
4
D
图形间的面积比较,往往牵涉到图形间的关系:如三角形的面积是与它等底等高的平行四边形面积的一半等。
我们还经常用到如下这些规律:
等底等高的平行四边形面积相等;
等底等高的三角形面积相等;
面积相等的平行四边形、三角形或梯形,形状不一定相同等。
知识点4:不规则图形面积的估算
4. 图中每个小方格的面积是1 cm?,涂色部分的面积约是多少平方厘米?
不规则图形面积的估算有两种方法:①数方格;
②转化为简单图形估算。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
方法① :数方格
S=28+28÷2
=42(cm2)
答:涂色部分的面积约是42 cm2。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
方法② :转化成三角形
S三角形=ah÷2
=10×8÷2
=40(cm2)
答:涂色部分的面积约是
40 cm? 。
4. 图中每个小方格的面积是1 cm?,涂色部分的面积约是多少平方厘米?
知识点5:认识平方千米与公顷
5.在( )里填上合适的数。
0.5 hm?=( )m? 0.0068 km?=( )m?
900 m?=( )hm?
70 hm?=( )km?
5000
6800
0.09
0.7
要牢记1 hm2=10000 m2 、
1 km2=1000000 m2 、1 km2=100 hm2 。
知识点6:计算有规律堆放原木总根数
(顶层根数+底层根数)×层数÷2
我们经常见到像这样堆放的圆木、钢管,通常用下面算法求总根数:
层数:20-2+1=19(层)
总根数:(2+20)×19÷2=209(根)
答:这堆木料一共有209根。
6.家具厂有一堆木料堆放如下图,已知最上面一层有2根木料,最下面一层有20根木料,上面一层总比下面一层
少1根,这堆木料一共有多少根?
我知道,此类题可以根据公式(顶层根数+底层根数)×层数÷2进行计算。
(1)平行四边形的面积一定比梯形的面积大 ( )
(2)平行四边形的面积等于三角形面积的2倍。 ( )
(3)梯形的上底、下底越长,面积越大。 ( )
(4)任何一个梯形都可以分成两个等高的三角形。( )
(5)两个面积相等的三角形,一定能拼成一个平行
四边形。 ( )
课堂练习
1. 判断下面各题的叙述是否正确。
√
×
×
×
×
2.新华村开垦了一块近似于平行四边形的荒地 (如图所示),如果每公顷能收9300 kg玉米,
这块地大约能收多少千克玉米?
(教材第96页练习二十五第5题)
荒地面积为:
140×350=49000(m?)=4.9(hm?)
这块地能收玉米:
4.9×9300=45570(kg)
答:这块地大约能收45570 kg玉米。
3.这块钢板重多少千克?
每平方分米钢板重0.4千克。
梯形面积:(8+16)×14÷2=168(dm?)
梯形钢板重:168×0.4=67.2(kg)
答:这块钢板重67.2 kg。
8 dm
14 dm
16 dm
(教材第96页练习二十五第6题)
4.如图,是教室的一面墙的示意图。如果砌这面墙平均每平方米用砖 185 块,一共需要用多少块砖?
看图可知,这面墙由一个三角形和一个长方形组成。先求面积,再求出共需用砖的块数。
长方形面积:5×4 = 20(m2)
三角形面积:1.2×5÷2 = 3(m2)
墙的面积:20+3 = 23(m2)
砖的块数:185×23 = 4255(块)
答:一共需要4255块砖。
5.有一台收割机,作业宽度是1.8 m。每小时行5 km, 大约多长时间可以收割完下边这块地?
200 m
330 m
100 m
先求这块地的面积,再计算出收割机的工作效率,最后算工作时间。
5 km=5000 m
1.8×5000=9000(m2)
(200+330)×100÷2=26500(m2)
26500÷9000 ≈ 2.94(h)
答:大约2.94 h可以收割完这块地。
6.图中每个小方格的边长是1 m,请你估算涂色部分的面积。
S=S满格+S不满格
=26+42÷2
=47(m2)
=26+21
答:涂色部分的面积大约是47 m2 。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
本题可采用数方格的方法进行估算。
课堂小结
通过复习我还掌握不规则图形面积的计算方法。同时对平移、旋转等知识在公式推导过程中的应用理解更深了。
通过整理与复习,我掌握了平行四边形、三角形和梯形的面积计算公式的推导和运用。
这节课你有什么收获?
