第二章 有 理数 第1讲 有理数与数轴 ( 讲义 课后练习 答案) 2021年暑假小升初衔接 北师大版数学七年级上册
文档属性
| 名称 | 第二章 有 理数 第1讲 有理数与数轴 ( 讲义 课后练习 答案) 2021年暑假小升初衔接 北师大版数学七年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 107.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-09 09:32:34 | ||
图片预览



文档简介
第一讲:有理数与数轴
知识导读:
、相关知识链接
我们在小学学习的数:
、自然数: 0,1, 2, 3,…;
、分数: 12,13,34,112,…;
、小数:0.5, 1.2, 0.25, 0.139, …;
、百分数:37%, 58%,…。
这种分类的标准是什么?
、生活中正负数及其运用。
、观察温度计,海拔高度的标尺,我们发现:正负数可以用直线上的点来表示。
、教材知识详解
负数的产生:具有相反意义的两个量,我们把其中的一个量用正数表示,与它意义相反的量就用负数表示,
减法运算:53-79=?
数学历史上的正负数:古代中国,印度,欧洲。
三国时代魏刘徽:“两算得失相反,要令正负以名之”,7-2=5,2-7=-5。
正数与负数的意义
有理数的意义
整数包括正整数、零、负整数:…,-4,-3,-2,-1,0,1,2,3,4,…
分数包括正分数和负分数:…2.129,0.8,34,-0.5,?23,?213,…
整数和分数统称为有理数。
注意:①有限小数是分数,无限循环小数是分数;
②任意一个有理数可以表示为最简分数 mn 的形式,
(m、n为互质数,n≠0)。
44850051841501732280107950 3、有理数的分类:
3637280139065 正整数 正整数
114173045085 整数 零 正有理数
负整数 正分数
1732280115570有理数 有理数 零
448500522225 分数 正分数 负整数
负分数 负有理数
负分数
备注:①正数和零又称为非负数,负数和零又称为非正数。
②圆周率π是无限不循环小数,不能用分数 mn表示,所以π不是有理数。
4、数轴的意义:
规定了原点,正方向,单位长度用来表示数的直线叫数轴。
546735121920● ● ● ● ● ● ●
-1 O 1
原点,正方向和单位长度叫数轴的三要素。
习惯上,数轴上向右的方向为正方向。
数轴上的点与有理数的关系:
任意一个有理数可以用数轴上的一点表示,数轴上的一部分点表示有理数;像圆周率π等,能用数轴上的点表示,所以数轴上的另一部分点表示有理数以外的数。
数轴是建立有理数与直线上点的联系的桥梁,有理数的有些问题可以在 直线上从几何方面来思考,如相反数、绝对值等。
二、知识运用
例1、下列关于“0”的说法中:①是整数:②是整数,但不是自然数;
③既不是正数又不是负数;④比正数小的数。其中正确的有 。
变式练习:
1、下列语句中正确的有( )个。
①所有整数都是正数; ② +0是正数;③ - 227是有理数;④在有理数中除了正数就是负数。
A、 1 B、 2 C、 3 D、 4
例2、把下列各数填入表示相应集合的大括号里:
-7.2, 34, -9, 1.4, 0,3.14,π, 1245, -2.5, 63, 0.708 。
整数集合:{ …}
正数集合:{ …}
分数集合:{ …}
有理数集合:{ …}
非正数集合:{ …}
负分数集合:{ …} 。
变式练习:
把下列各数分别填在相应的集合中:
- 52 , 0, -1, 0.73, 2, -5, 78, -29.52, +28, 2-π, π3, 0.7+3
(1)正数集合:{ …}
(2)负数集合:{ …}
(3)整数集合:{ …}
(4)分数集合:{ …}
(5)有理数集合:{ …} 。
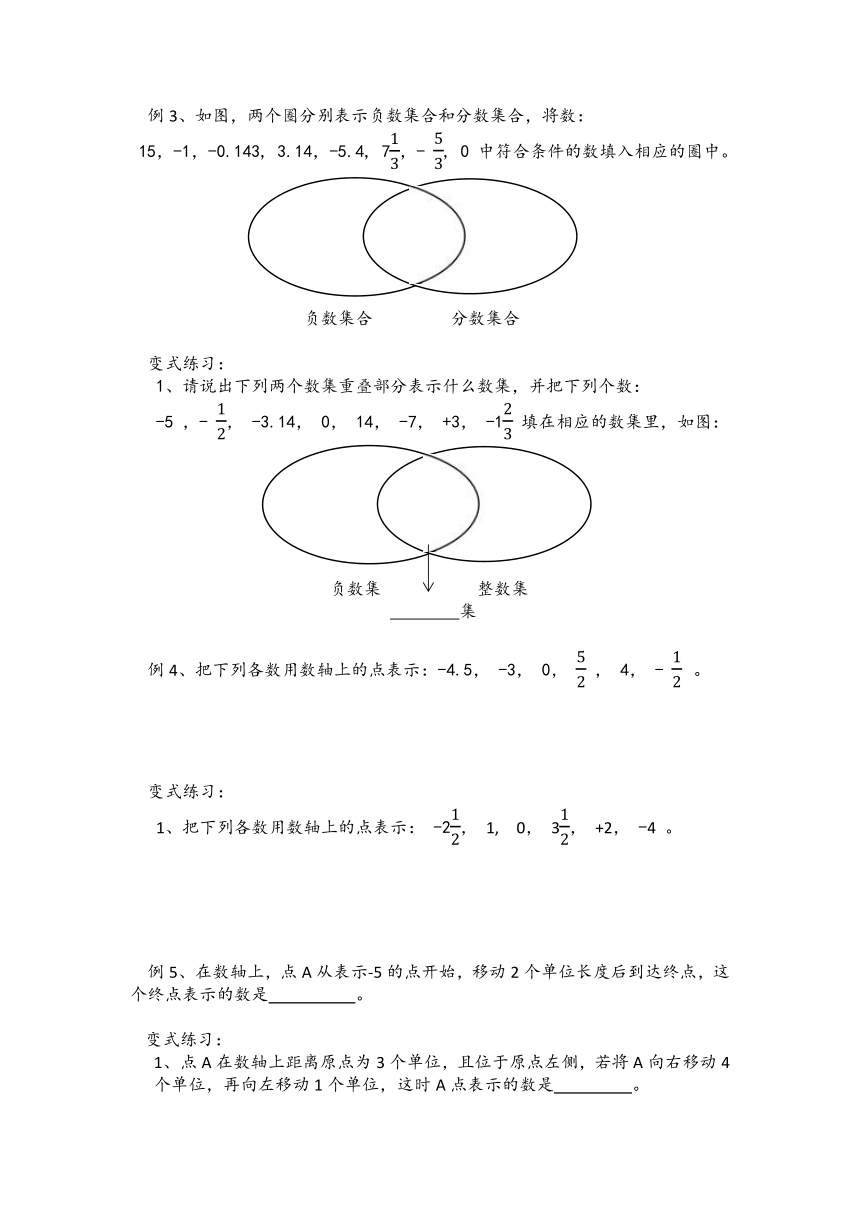
例3、如图,两个圈分别表示负数集合和分数集合,将数:
15,-1,-0.143, 3.14,-5.4, 713,- 53, 0 中符合条件的数填入相应的圈中。
104203554610
负数集合 分数集合
变式练习:
请说出下列两个数集重叠部分表示什么数集,并把下列个数:
1165860427990-5 ,- 12, -3.14, 0, 14, -7, +3, -123 填在相应的数集里,如图:
2623185109220
负数集 整数集
集
把下列各数用数轴上的点表示:-4.5, -3, 0, 52 , 4, - 12 。
变式练习:
把下列各数用数轴上的点表示: -212, 1, 0, 312, +2, -4 。
在数轴上,点A从表示-5的点开始,移动2个单位长度后到达终点,这个终点表示的数是 。
变式练习:
点A在数轴上距离原点为3个单位,且位于原点左侧,若将A向右移动4个单位,再向左移动1个单位,这时A点表示的数是 。
观察下面一列数,按规律在横线上填写适当的数:
12, - 36, 512,- 720, , ,…。
变式练习:
观察下面一组数据,探求其中规律:
- 12, 23,- 34, 45,- 56, 67,…
、填出第7、8、9项的三个数;
、第2021个数是什么?
、如果这组数据无限排列下去,与哪两个数越来越近?
课后练习:
知识与技能
选择:
下列说法中正确的有( )个。
① 0是整数;② -113是负分数;③ 3.2不是正数;
④ 自然数一定是正数;⑤负分数一定是负有理数。
A、 1 B、 2 C、 3 D、 4
2、下列说法中正确的是( )。
A、正整数和负整数统称为整数, B、正有理数和负有理数统称为有理数,
C、整数和分数统称为有理数, D、非负有理数就是正有理数。
二、填空:
3、非负整数与正整数的区别是非负整数包括 ,而正整数不包括 。
4、在有理数-4.2, 6, 0,-11,- 227,- 124,0.79中,分数有 。
5、数轴上A,B两点,如果点A对应的数是-2,且A,B两点的距离为3,那么点B对应的数是 。
6、数轴上到原点的距离小于3的整数的个数为x,不大于3的整数的个数为y,等于3的整数的个数为z,则x + y + z = 。
核心能力
7、小明写作业时不慎将墨水滴在数轴上,请根据图中的数值,判断墨迹盖住部分的整数有 个。
高速公路上,从3千米处开始,每隔4千米经过一个限速标志牌,并且从10千米处开始,每隔9千米经过一个速度监控仪,司机小王刚好在19千米的A处第一次同时经过这两种设施,那么,司机小王第二次同时经过这两种设施需要从A处继续行驶( )千米。
A、36 B、37 C、55 D、91
点A,B分别是数 -3,- 12在数轴上对应的点,将线段AB沿数轴向右移动到A’B’,且线段A’B’的中点对应的数是3,则A’对应的数是 ,点A移动的距离是 。
一列数: 11,- 12,22,- 12,13,- 23,33,- 23,13,- 14,24,- 34,…
711 是第几个数?
第400个数是什么?
11、请把大括号内表示的A、B、C三个数集中的数填在如图所示圈内的位置。
A={ -8,-6, -5, 1, 2 };
B={ -5,- 23,- 13,2,3 };
C={ -15, -5,1,3, 8 }。
12、已知数轴上A、B两点对应数分别为-2和4,P为数轴上一点,对应数为x。
(1)、若P为线段AB的三等分点,求P点对应的数,
、在数轴上是否存在一点P,使P到A、B的距离和等于10 ? 若存在,求出x的值;若不存在,请说明理由。
答案:
①③④ 变式练习: 1、 A
例2、解:整数集合:{ -9, 0, 63 }
正数集合:{ 34 , 1.4, 3.14, π, 1245,63,0.708 }
分数集合:{ -7.2, 34 , 1.4, 3.14, 1245,-2.5,0.708 }
有理数集合:{-7.2,34 , -9,1.4,0,3.14,1245,-2.5,63,0.708 }
非正数集合:{ -7.2, -9, 0, -2.5 }
负分数集合:{ -7.2, -2.5 }
变式练习:
解:正数集合:{ 0.73, 2,78 ,+28,π3,0.7+3 }
负数集合:{ - 52,-1, -5, -29.53, 2-π}
整数集合:{ 0, -1, 2, -5, +28 }
分数集合:{ - 52, 0.73,78 ,-29.53,0.7+3 }
有理数集:{- 52,0,-1, 0.73,2, -5, 78 ,-29.53,+28, 0.7+3 }
851535115570例3、
-1
-0.143 -5.4 3.14
- 53 713
负数集合 分数集合
946785233680变式练习:
- 12,-3.14 -5 0, 14
2394585331470 - 123 -7 +3
负数集 整数集
负整数集
略 变式练习: 略
-7,-3 变式练习: 0
解:930 , - 1142
变式练习:(1) - 78 89 - 910 (2)- 20212022 (3)、-1,+1
课后练习:
C 2、 C 3、 0 ,0
4、-4.2,- 227, 0.79 5、-5或1 6、 14
7、 9 8、 A 9、 74 ,194
10、解:(1)、分母小于11的合计1+3+5+…+19=100,所以711 排第107或者第100+21-6=115.
(2)、分母小于21的合计1+3+5+…+39=400,所以排第400个数为- 120.
11、解:
103822543815
-8,-6 2 - 13,- 23
1 -5 3
-15, 8
12、解:(1)、 0或2
(2)、 x=-4或6时,PA+PB=10.
知识导读:
、相关知识链接
我们在小学学习的数:
、自然数: 0,1, 2, 3,…;
、分数: 12,13,34,112,…;
、小数:0.5, 1.2, 0.25, 0.139, …;
、百分数:37%, 58%,…。
这种分类的标准是什么?
、生活中正负数及其运用。
、观察温度计,海拔高度的标尺,我们发现:正负数可以用直线上的点来表示。
、教材知识详解
负数的产生:具有相反意义的两个量,我们把其中的一个量用正数表示,与它意义相反的量就用负数表示,
减法运算:53-79=?
数学历史上的正负数:古代中国,印度,欧洲。
三国时代魏刘徽:“两算得失相反,要令正负以名之”,7-2=5,2-7=-5。
正数与负数的意义
有理数的意义
整数包括正整数、零、负整数:…,-4,-3,-2,-1,0,1,2,3,4,…
分数包括正分数和负分数:…2.129,0.8,34,-0.5,?23,?213,…
整数和分数统称为有理数。
注意:①有限小数是分数,无限循环小数是分数;
②任意一个有理数可以表示为最简分数 mn 的形式,
(m、n为互质数,n≠0)。
44850051841501732280107950 3、有理数的分类:
3637280139065 正整数 正整数
114173045085 整数 零 正有理数
负整数 正分数
1732280115570有理数 有理数 零
448500522225 分数 正分数 负整数
负分数 负有理数
负分数
备注:①正数和零又称为非负数,负数和零又称为非正数。
②圆周率π是无限不循环小数,不能用分数 mn表示,所以π不是有理数。
4、数轴的意义:
规定了原点,正方向,单位长度用来表示数的直线叫数轴。
546735121920● ● ● ● ● ● ●
-1 O 1
原点,正方向和单位长度叫数轴的三要素。
习惯上,数轴上向右的方向为正方向。
数轴上的点与有理数的关系:
任意一个有理数可以用数轴上的一点表示,数轴上的一部分点表示有理数;像圆周率π等,能用数轴上的点表示,所以数轴上的另一部分点表示有理数以外的数。
数轴是建立有理数与直线上点的联系的桥梁,有理数的有些问题可以在 直线上从几何方面来思考,如相反数、绝对值等。
二、知识运用
例1、下列关于“0”的说法中:①是整数:②是整数,但不是自然数;
③既不是正数又不是负数;④比正数小的数。其中正确的有 。
变式练习:
1、下列语句中正确的有( )个。
①所有整数都是正数; ② +0是正数;③ - 227是有理数;④在有理数中除了正数就是负数。
A、 1 B、 2 C、 3 D、 4
例2、把下列各数填入表示相应集合的大括号里:
-7.2, 34, -9, 1.4, 0,3.14,π, 1245, -2.5, 63, 0.708 。
整数集合:{ …}
正数集合:{ …}
分数集合:{ …}
有理数集合:{ …}
非正数集合:{ …}
负分数集合:{ …} 。
变式练习:
把下列各数分别填在相应的集合中:
- 52 , 0, -1, 0.73, 2, -5, 78, -29.52, +28, 2-π, π3, 0.7+3
(1)正数集合:{ …}
(2)负数集合:{ …}
(3)整数集合:{ …}
(4)分数集合:{ …}
(5)有理数集合:{ …} 。
例3、如图,两个圈分别表示负数集合和分数集合,将数:
15,-1,-0.143, 3.14,-5.4, 713,- 53, 0 中符合条件的数填入相应的圈中。
104203554610
负数集合 分数集合
变式练习:
请说出下列两个数集重叠部分表示什么数集,并把下列个数:
1165860427990-5 ,- 12, -3.14, 0, 14, -7, +3, -123 填在相应的数集里,如图:
2623185109220
负数集 整数集
集
把下列各数用数轴上的点表示:-4.5, -3, 0, 52 , 4, - 12 。
变式练习:
把下列各数用数轴上的点表示: -212, 1, 0, 312, +2, -4 。
在数轴上,点A从表示-5的点开始,移动2个单位长度后到达终点,这个终点表示的数是 。
变式练习:
点A在数轴上距离原点为3个单位,且位于原点左侧,若将A向右移动4个单位,再向左移动1个单位,这时A点表示的数是 。
观察下面一列数,按规律在横线上填写适当的数:
12, - 36, 512,- 720, , ,…。
变式练习:
观察下面一组数据,探求其中规律:
- 12, 23,- 34, 45,- 56, 67,…
、填出第7、8、9项的三个数;
、第2021个数是什么?
、如果这组数据无限排列下去,与哪两个数越来越近?
课后练习:
知识与技能
选择:
下列说法中正确的有( )个。
① 0是整数;② -113是负分数;③ 3.2不是正数;
④ 自然数一定是正数;⑤负分数一定是负有理数。
A、 1 B、 2 C、 3 D、 4
2、下列说法中正确的是( )。
A、正整数和负整数统称为整数, B、正有理数和负有理数统称为有理数,
C、整数和分数统称为有理数, D、非负有理数就是正有理数。
二、填空:
3、非负整数与正整数的区别是非负整数包括 ,而正整数不包括 。
4、在有理数-4.2, 6, 0,-11,- 227,- 124,0.79中,分数有 。
5、数轴上A,B两点,如果点A对应的数是-2,且A,B两点的距离为3,那么点B对应的数是 。
6、数轴上到原点的距离小于3的整数的个数为x,不大于3的整数的个数为y,等于3的整数的个数为z,则x + y + z = 。
核心能力
7、小明写作业时不慎将墨水滴在数轴上,请根据图中的数值,判断墨迹盖住部分的整数有 个。
高速公路上,从3千米处开始,每隔4千米经过一个限速标志牌,并且从10千米处开始,每隔9千米经过一个速度监控仪,司机小王刚好在19千米的A处第一次同时经过这两种设施,那么,司机小王第二次同时经过这两种设施需要从A处继续行驶( )千米。
A、36 B、37 C、55 D、91
点A,B分别是数 -3,- 12在数轴上对应的点,将线段AB沿数轴向右移动到A’B’,且线段A’B’的中点对应的数是3,则A’对应的数是 ,点A移动的距离是 。
一列数: 11,- 12,22,- 12,13,- 23,33,- 23,13,- 14,24,- 34,…
711 是第几个数?
第400个数是什么?
11、请把大括号内表示的A、B、C三个数集中的数填在如图所示圈内的位置。
A={ -8,-6, -5, 1, 2 };
B={ -5,- 23,- 13,2,3 };
C={ -15, -5,1,3, 8 }。
12、已知数轴上A、B两点对应数分别为-2和4,P为数轴上一点,对应数为x。
(1)、若P为线段AB的三等分点,求P点对应的数,
、在数轴上是否存在一点P,使P到A、B的距离和等于10 ? 若存在,求出x的值;若不存在,请说明理由。
答案:
①③④ 变式练习: 1、 A
例2、解:整数集合:{ -9, 0, 63 }
正数集合:{ 34 , 1.4, 3.14, π, 1245,63,0.708 }
分数集合:{ -7.2, 34 , 1.4, 3.14, 1245,-2.5,0.708 }
有理数集合:{-7.2,34 , -9,1.4,0,3.14,1245,-2.5,63,0.708 }
非正数集合:{ -7.2, -9, 0, -2.5 }
负分数集合:{ -7.2, -2.5 }
变式练习:
解:正数集合:{ 0.73, 2,78 ,+28,π3,0.7+3 }
负数集合:{ - 52,-1, -5, -29.53, 2-π}
整数集合:{ 0, -1, 2, -5, +28 }
分数集合:{ - 52, 0.73,78 ,-29.53,0.7+3 }
有理数集:{- 52,0,-1, 0.73,2, -5, 78 ,-29.53,+28, 0.7+3 }
851535115570例3、
-1
-0.143 -5.4 3.14
- 53 713
负数集合 分数集合
946785233680变式练习:
- 12,-3.14 -5 0, 14
2394585331470 - 123 -7 +3
负数集 整数集
负整数集
略 变式练习: 略
-7,-3 变式练习: 0
解:930 , - 1142
变式练习:(1) - 78 89 - 910 (2)- 20212022 (3)、-1,+1
课后练习:
C 2、 C 3、 0 ,0
4、-4.2,- 227, 0.79 5、-5或1 6、 14
7、 9 8、 A 9、 74 ,194
10、解:(1)、分母小于11的合计1+3+5+…+19=100,所以711 排第107或者第100+21-6=115.
(2)、分母小于21的合计1+3+5+…+39=400,所以排第400个数为- 120.
11、解:
103822543815
-8,-6 2 - 13,- 23
1 -5 3
-15, 8
12、解:(1)、 0或2
(2)、 x=-4或6时,PA+PB=10.
同课章节目录
