六年级上册数学课件-回顾整理—— 总复习 图形与几何、统计与概率-青岛版(17张ppt)
文档属性
| 名称 | 六年级上册数学课件-回顾整理—— 总复习 图形与几何、统计与概率-青岛版(17张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-10 14:48:48 | ||
图片预览


文档简介
图形与几何、统计与概率
青岛版数学六年级(上)
回顾整理
——总复习
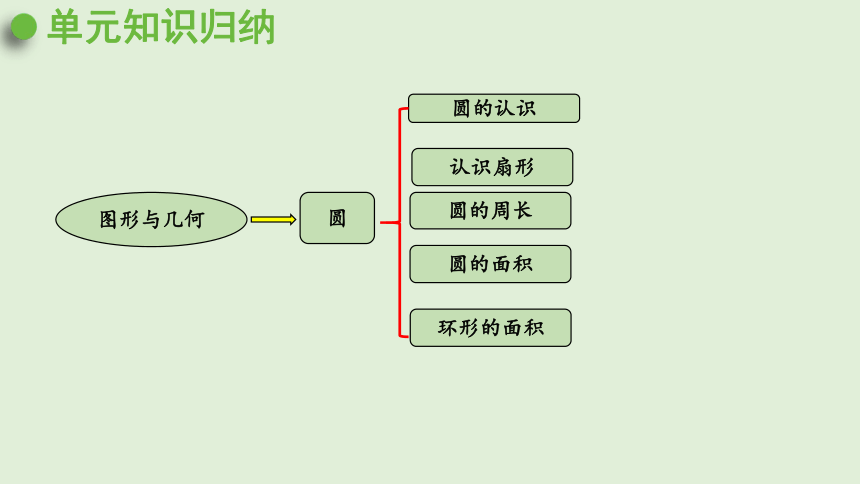
图形与几何
圆
圆的周长
圆的面积
圆的认识
环形的面积
认识扇形
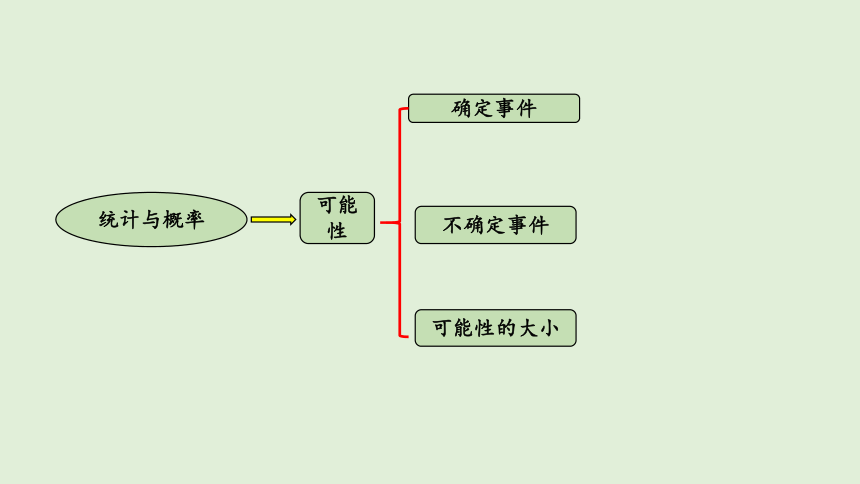
统计与概率
可能性
可能性的大小
确定事件
不确定事件
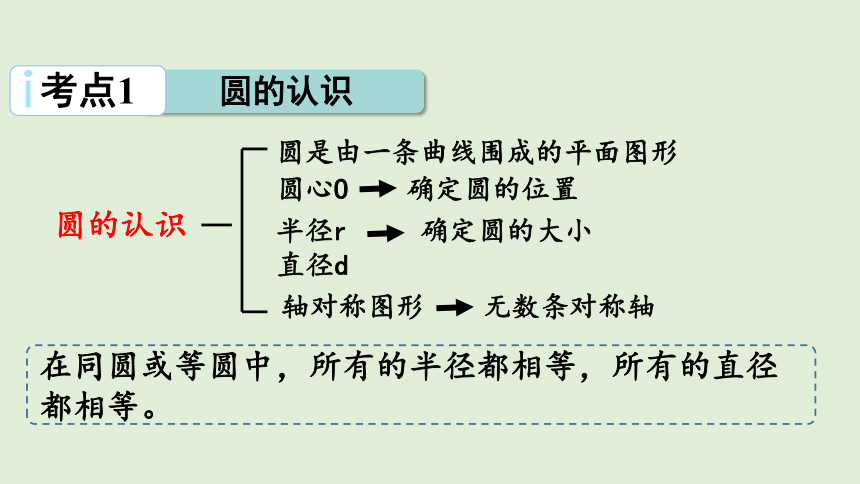
圆的认识
考点1
圆心O 确定圆的位置
半径r 确定圆的大小
直径d
轴对称图形 无数条对称轴
圆的认识
圆是由一条曲线围成的平面图形
在同圆或等圆中,所有的半径都相等,所有的直径都相等。
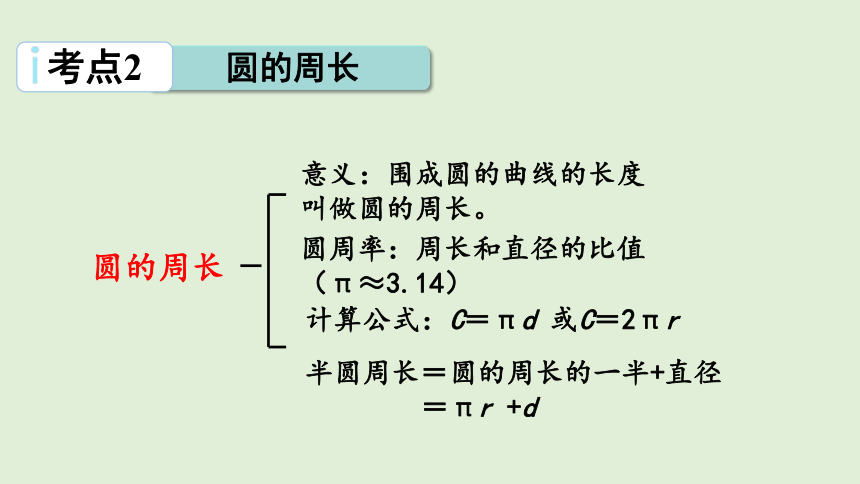
圆的周长
考点2
圆的周长
意义:围成圆的曲线的长度叫做圆的周长。
圆周率:周长和直径的比值
(π≈3.14)
计算公式:C=πd 或C=2πr
半圆周长=圆的周长的一半+直径
=πr +d
圆的面积
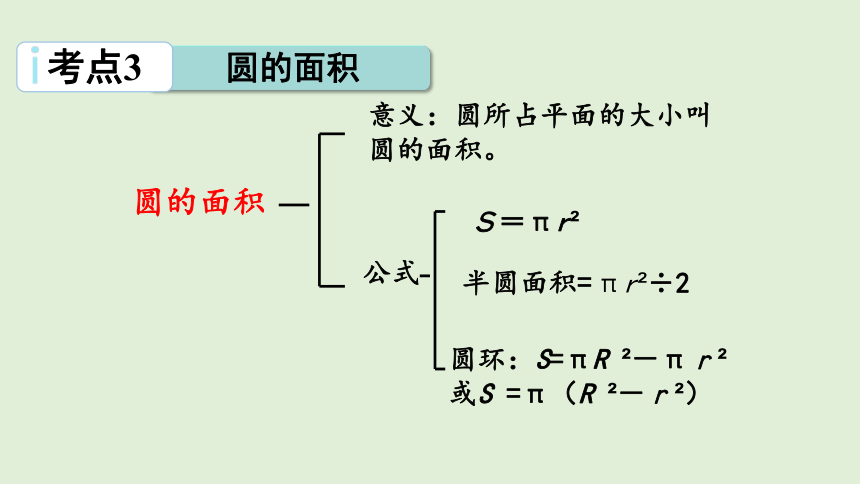
考点3
圆的面积
意义:圆所占平面的大小叫
圆的面积。
公式
S=πr?
圆环:S=πR ?-πr? 或S =π(R ?-r?)
半圆面积=
πr?÷2
可能性
考点4
1.有些事情的发生时确定的,有些则是不确定的。不确定事件发生的可能性有大有小。
2.不确定事件发生的可能性大小与事件的数量的多少有关,所占数量越多,可能性就越大,所占数量越少,可能性就越小。
指针指向哪个区域是一个随机事件,指向任何区域的可能性都有。
指针指向黄色区域的可能性最小。
任意转动转盘,转盘停止时,指针可
能指向什么颜色区域?指向指向哪个
区域的可能性最小?
举例
nn蜜蜂大多在离巢2.5千米的圆周内采蜜,采蜜的范围大约是多少平方千米?
1
3.14×2.5
2
= 3.14×6.25
= 19.625(平方千米)
答:采蜜的范围大约是19.625平方千米。
(教材第108页第25题)
2
求下面涂色部分的面积。
= 21.5(平方厘米)
= 100-314÷4
10-3.14×10 ÷4
2
2
20÷2=10(厘米)
20 ×10-3.14× ×2
( )
2
2
10
= 200-3.14×25×2
= 43(平方厘米)
(教材第109页第26题)
2
如图,你能求出这个圆的周
长是多少米吗?
3
(教材第109页第28题)
= 3.14×4
= 12.56(米)
3.14×(2×2)
答:这个圆的周长是12.56米。
一根铁丝可以围成一个半径是6厘米的圆。如果把这根铁丝重新围成正方形,这个正方形的边长是多少厘米?
4
想一想:铁丝由圆转化成正方形后,什么没有发生变化?
知道圆形铁丝的半径可以求出圆形的什么?
怎样求正方形边长?
3.14×6×2=37.68(厘米)
37.68÷4=9.42(厘米)
答:这个正方形的边长是9.42厘米。
(教材第109页第29题)
公园里有一个圆形花坛,直径是18米,在花坛的周围修一条1米宽的环形石子路。
(1)这条石子路的面积是多少平方米?
5
3.14×102
3.14×92
-
=3.14×100
-
3.14×81
=59.66(平方米)
=3.14×(100
-
81)
=3.14×19
答:石子路的面积是59.66平方米。
外圆半径:18÷2+1=10(米)
内圆半径:18÷2=9(米)
(教材第110页第32题)
6
填一填。
(1)画圆时,圆规两脚间的距离就是圆的( )。
(2)圆中最长的线段是圆的( )。
(3)圆的半径与它的直径的比是( )。
(4)把一个圆形纸片沿半径平均分成若干等份,拼成一个近似的长方形。则面积( ),周长( )。
(5)在一个长6厘米,宽4厘米的长方形中,画一个最大的圆, 这个圆的面积是( )平方厘米。
半径
直径
1:2
不变
变大
12.56
从下面某个盒子里摸了15次球
(每次摸出后再放入盒中摇匀),
摸出球的情况如右表。
小红最有可能是从哪个盒子里摸的球?
7
2个黄球
8个白球
5个黄球
5个白球
8个黄球
2个白球
①
②
③
答:小红最有可能从3号盒子里摸的球。因为3号盒子里摸到黄球的可能性大,摸到白球的可能性小。
8
连一连。
8个白球
8个黄球
8个红球
6个黄球,
2个红球
2个黄球,
6个红球
4个黄球,
4个红球
一定是红球
摸到红球和黄球的可能性一样大
摸到红球的可能性小
8个红球
4个黄球,
4个红球
不可能是红球
摸到红球的可能性大
作业课件中的相关练习。
青岛版数学六年级(上)
回顾整理
——总复习
图形与几何
圆
圆的周长
圆的面积
圆的认识
环形的面积
认识扇形
统计与概率
可能性
可能性的大小
确定事件
不确定事件
圆的认识
考点1
圆心O 确定圆的位置
半径r 确定圆的大小
直径d
轴对称图形 无数条对称轴
圆的认识
圆是由一条曲线围成的平面图形
在同圆或等圆中,所有的半径都相等,所有的直径都相等。
圆的周长
考点2
圆的周长
意义:围成圆的曲线的长度叫做圆的周长。
圆周率:周长和直径的比值
(π≈3.14)
计算公式:C=πd 或C=2πr
半圆周长=圆的周长的一半+直径
=πr +d
圆的面积
考点3
圆的面积
意义:圆所占平面的大小叫
圆的面积。
公式
S=πr?
圆环:S=πR ?-πr? 或S =π(R ?-r?)
半圆面积=
πr?÷2
可能性
考点4
1.有些事情的发生时确定的,有些则是不确定的。不确定事件发生的可能性有大有小。
2.不确定事件发生的可能性大小与事件的数量的多少有关,所占数量越多,可能性就越大,所占数量越少,可能性就越小。
指针指向哪个区域是一个随机事件,指向任何区域的可能性都有。
指针指向黄色区域的可能性最小。
任意转动转盘,转盘停止时,指针可
能指向什么颜色区域?指向指向哪个
区域的可能性最小?
举例
nn蜜蜂大多在离巢2.5千米的圆周内采蜜,采蜜的范围大约是多少平方千米?
1
3.14×2.5
2
= 3.14×6.25
= 19.625(平方千米)
答:采蜜的范围大约是19.625平方千米。
(教材第108页第25题)
2
求下面涂色部分的面积。
= 21.5(平方厘米)
= 100-314÷4
10-3.14×10 ÷4
2
2
20÷2=10(厘米)
20 ×10-3.14× ×2
( )
2
2
10
= 200-3.14×25×2
= 43(平方厘米)
(教材第109页第26题)
2
如图,你能求出这个圆的周
长是多少米吗?
3
(教材第109页第28题)
= 3.14×4
= 12.56(米)
3.14×(2×2)
答:这个圆的周长是12.56米。
一根铁丝可以围成一个半径是6厘米的圆。如果把这根铁丝重新围成正方形,这个正方形的边长是多少厘米?
4
想一想:铁丝由圆转化成正方形后,什么没有发生变化?
知道圆形铁丝的半径可以求出圆形的什么?
怎样求正方形边长?
3.14×6×2=37.68(厘米)
37.68÷4=9.42(厘米)
答:这个正方形的边长是9.42厘米。
(教材第109页第29题)
公园里有一个圆形花坛,直径是18米,在花坛的周围修一条1米宽的环形石子路。
(1)这条石子路的面积是多少平方米?
5
3.14×102
3.14×92
-
=3.14×100
-
3.14×81
=59.66(平方米)
=3.14×(100
-
81)
=3.14×19
答:石子路的面积是59.66平方米。
外圆半径:18÷2+1=10(米)
内圆半径:18÷2=9(米)
(教材第110页第32题)
6
填一填。
(1)画圆时,圆规两脚间的距离就是圆的( )。
(2)圆中最长的线段是圆的( )。
(3)圆的半径与它的直径的比是( )。
(4)把一个圆形纸片沿半径平均分成若干等份,拼成一个近似的长方形。则面积( ),周长( )。
(5)在一个长6厘米,宽4厘米的长方形中,画一个最大的圆, 这个圆的面积是( )平方厘米。
半径
直径
1:2
不变
变大
12.56
从下面某个盒子里摸了15次球
(每次摸出后再放入盒中摇匀),
摸出球的情况如右表。
小红最有可能是从哪个盒子里摸的球?
7
2个黄球
8个白球
5个黄球
5个白球
8个黄球
2个白球
①
②
③
答:小红最有可能从3号盒子里摸的球。因为3号盒子里摸到黄球的可能性大,摸到白球的可能性小。
8
连一连。
8个白球
8个黄球
8个红球
6个黄球,
2个红球
2个黄球,
6个红球
4个黄球,
4个红球
一定是红球
摸到红球和黄球的可能性一样大
摸到红球的可能性小
8个红球
4个黄球,
4个红球
不可能是红球
摸到红球的可能性大
作业课件中的相关练习。
同课章节目录
