2.1整式复习课件 2021-2022学年 人教版七年级数学上册(第一课时 28张)
文档属性
| 名称 | 2.1整式复习课件 2021-2022学年 人教版七年级数学上册(第一课时 28张) |  | |
| 格式 | pptx | ||
| 文件大小 | 980.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-09 10:26:18 | ||
图片预览








文档简介
2.1 整 式
第1课时 用字母表示数
用字母表示数可以简明地表达问题中的数量关系,如笼子里关着5只鸡,3只兔,共有_______个头,________条腿.如果笼子里关着x只鸡,y只兔,那么共有__________个头,__________条腿.用字母表示数量关系时,要注意:(1) 在同一个问题中,相同字母所表示的量必须相同,不同字母一般表示不同的量;(2) 在同一个问题中,不同的量必须用不同的字母表示;(3) 在不同的问题中,同一个字母可以表示不同的量.
8
22
(x+y)
(2x+4y)
1. 下列含有字母的式子中,符合书写要求的是 ( )
A. ab÷2 B. ab3 C. 12xy D. 234mn
2. 七(1)班男生有a人,女生人数比男生的一半多4,则女生人数是 ( )
A. 12(a+4) B. 12(a-4) C. 12a+4 D. 12a-4
3. 列式表示:
(1) x的2倍与5的差是________;
(2) 比m的32倍大3的数是________;
(3) 小明今年m岁,小明比小丽大2岁,小丽今年_________岁;
(4) 小红家到学校的距离是1 000 m,她步行的速度是v m/min,她走了
t min还未到学校,此时她离学校的距离为_____________m.
?
C
C
2x-5
32m+3
?
(m-2)
(1 000-vt)
4. 为适应小班化教学,需要定制一批新课桌,要求一张桌面配三条桌腿.
现在工人师傅已经生产了a张桌面,则需生产________条桌腿才能正好
配套.
5. (2020·长春)长春市净月潭国家森林公园门票价格为成人票每张30元,
儿童票每张15元,若购买m张成人票和n张儿童票,则共需花费
____________元.
6. 某市出租车的收费标准:起步价为12.50元,3千米后每千米收费2.40元
(不足1千米按1千米算).某人在该市乘坐出租车行驶x千米(x>3,且x
为整数),试用含x的式子表示他应付的费用,并求当x=8时,他应付的
费用.
3a
(30m+15n)
7. 一批上衣的进价为每件a元,在进价的基础上提高50%后作为售价,现由
于季节原因,打六折促销,则打折后每件上衣的价格为 ( )
A. a元 B. 0.9a元 C. 0.92a元 D. 1.04a元
8. 已知m是两位数,n是一位数,把m直接写在n后面,就成为一个三位数,
这个三位数可表示为 ( )
A. 10n+m B. nm C. n+10m D. 100n+m
9. 某商店举办促销活动,促销的方法是将原价x元的衣服以(45x-10)元出
售,则下列说法中,能正确表达该商店促销方法的是 ( )
A. 原价减去10元后再打八折 B. 原价打八折后再减去10元
C. 原价减去10元后再打两折 D. 原价打两折后再减去10元
?
B
D
B
10. (1) 已知一个长方体的长和宽都为m,高为312,则它的体积为________.
(2) 若n表示整数,则三个连续的整数一般可写为__________________,
________,_______;三个连续的偶数一般可写为________,________,
________;三个连续的奇数一般可写为_______,________,________.
(3) 若一个两位数的十位上的数字为x,个位上的数字为y,则这个两位
数可表示为________;若把这个两位数的十位上的数字与个位上的数字
颠倒位置,则此时的两位数可表示为________.
(4) 观察下列一组数:14,39,516,725,936,…,它们是按一定的规律排
列的,那么这一组数的第n(n为正整数)个数是__________.
?
72m2
?
答案不唯一,如n
n+1
n+2
2n-2
2n
2n+2
2n-1
2n+1
2n+3
10x+y
10y+x
2n?1(n+1)2
?
11. 某书店出售图书的同时,推出一项租书业务,每租看1本书,租期不超
过3天,每天租金a元;租期超过3天,从第4天开始每天另加收b元.如
果租看1本书,租期为7天,那么租金为_________________________元.
12. 如图,用4根火柴棒可搭出1个小正方形,用7根火柴棒可搭出2个小正
方形,按照这样的方式,搭3个小正方形需用________根火柴棒,搭4
个小正方形需用________根火柴棒,搭n(n为正整数)个小正方形需用
________根火柴棒,搭100个小正方形需用________根火柴棒.
[3a+4(a+b)][或(7a+4b)]
10
13
(3n+1)
301
第12题
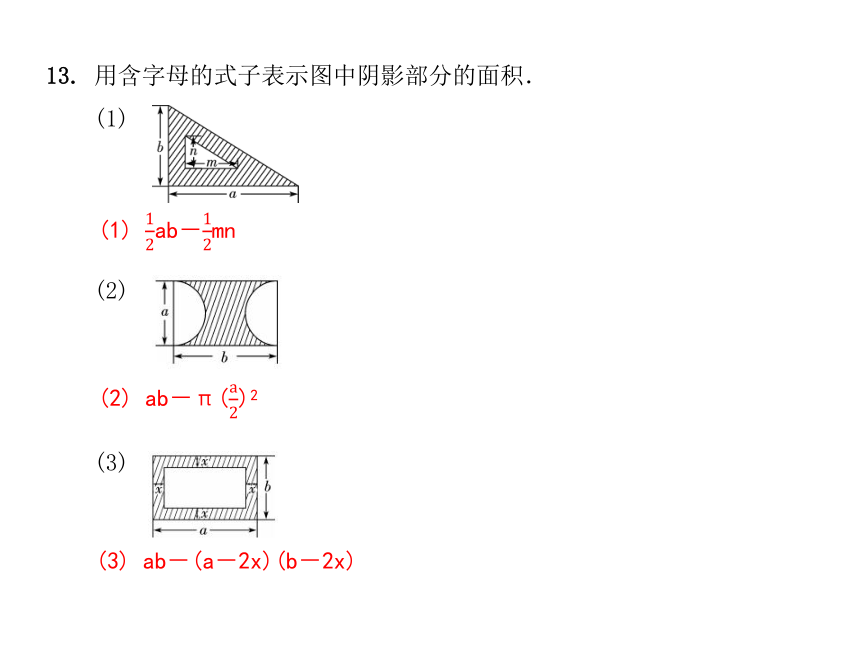
13. 用含字母的式子表示图中阴影部分的面积.
(1)
(2)
(3)
(1) 12ab-12mn
?
(2) ab-π(a2)2
?
(3) ab-(a-2x)(b-2x)
14. 观察下列各式:21×2=21+2;32×3=32+3;43×4=43+4;54×5=54+5;
….请你将猜想到的规律用含字母n(n为正整数)的式子表示出来.
?
第2课时 单 项 式
1. 单项式:表示数或字母的________的式子叫做单项式.特别地,单独的
一个数或一个字母也是单项式.
2. 单项式的系数:单项式中的____________叫做这个单项式的系数.
3. 单项式的次数:一个单项式中,所有字母的指数的________叫做这个单
项式的次数.对于单独一个非零的数,规定它的次数为________.
积
数字因数
和
0
1. (2020·日照)单项式-3ab的系数是 ( )
A. 3 B. -3 C. 3a D. -3a
2. 下列语句错误的是 ( )
A. 数字0也是单项式 B. 单项式-a的系数与次数都是1
C. 12xy是二次单项式 D. -2ab3的系数是-23
3. 有下列式子:-2x2,ax,1x,113x,1+a,-b,3+2a,x+y2.其中,单项
式共有 ( )
A. 2个 B. 4个 C. 6个 D. 8个
4. (2019·黄冈)-12x2y是________次单项式.
?
B
B
B
三
?
6. 下列各组单项式中,次数相同的是 ( )
A. 2ab与4xy2 B. 3π与a
C. 13x2y2与xy D. a3与xy2
7. 已知单项式-3xmy37的次数是7,则2m-17的值是 ( )
A. 8 B. -8 C. 9 D. -9
8. 已知(a-1)x2ya+1是关于x,y的五次单项式,则这个单项式的系数是
( )
A. 1 B. 2 C. 3 D. 0
?
D
D
A
9. 单项式-512xy3的系数是m,次数是n,则mn=________.
10. 若单项式-x4ymz和5a5bn都是六次单项式,则m+n=________.
11. 如果|a+2|+(b-3)2=0,那么单项式-xa+byb-a的次数是________.
12. 邮购一种书,每册书的定价为a元,另加书价的10%作为邮资.邮购这
种书n册,总计金额为y元,则y=________;当a=10.8,n=50时,y
的值为________.
13. 填表:
?
-53
?
2
6
1.1an
594
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}单项式
-15a2b
43ab2c
-0.15m
????3????47
系 数
?
?
?
?
次 数
?
?
?
?
-15
43
?
-0.15
17
?
3
4
1
7
14. 列出单项式,并指出它们的系数和次数:
(1) 某班的总人数为m,女生人数是男生人数的35,则该班的男生人数
为多少?
(2) 某班学生按横m纵n排列座次且坐满,则该班的学生人数为多少?
(3) 一辆汽车的速度为x千米/时,则该汽车行驶40分钟的路程为多少
千米?
(4) 学校购买了一批图书,共a箱,每箱有b册,将这批图书的一半捐
给社区,捐给社区的图书有多少册?
(5) 一个直角三角形的一条直角边长x cm,另一条直角边长9 cm,求
该直角三角形的面积.
?
15. 已知单项式-23xy2m-1与-22x2y2的次数相同.
(1) 求m的值;
(2) 当x=-9,y=-2时,求单项式-23xy2m-1的值.
?
16. 观察下列单项式:-x,2x2,-3x3,…,-19x19,20x20,….
(1) 根据你发现的规律,写出第101个和第102个单项式;
(2) 请写出第n(n为正整数)个单项式.
第3课时 多项式及整式
1. 多项式:几个单项式的________叫做多项式.其中,每个单项式叫做多
项式的________,不含字母的项叫做__________.
2. 多项式的次数:多项式里,次数________项的次数,叫做这个多项式的
次数.
3. 整式:________与________统称整式.
和
项
常数项
最高
单项式
多项式
1. 多项式-2a3b+3a2-4的项数及次数分别是 ( )
A. 3,3 B. 4,3
C. 3,4 D. 3,6
2. 将多项式3x2y-xy2+x3y3-x4y4-1按字母x的降幂排列,则下列各式正
确的是 ( )
A. -1-xy2+3x2y+x3y3-x4y4
B. -x4y4+x3y3+3x2y-xy2-1
C. -x4y4+x3y3-xy2+3x2y-1
D. -1+3x2y-xy2+x3y3-x4y4
C
B
3. 多项式-12x+3x2-5的次数最高项是________,一次项系数是_______,
常数项是________.
4. 小李有a2本书,小张把自己的书给了小李2a本后,他们两人书的数量相
同,则小张原来有书___________本,这是一个______次多项式.
5. 若多次项4xn+2-5x2-n+6是关于x的三次多项式,求n2-2n+3的值.
?
3x2
-12
?
-5
(a2+4a)
二
6. 小明房间的窗户如图所示,其中上方的装饰物由两个四分之一圆和一个
半圆组成(它们的半径相同).
(1) 装饰物所占的面积是多少?窗户中能射进阳光的部分的面积是多少
(窗框的面积忽略不计)?
(2) 观察(1)中所得到的结果,它们是单项式还是多项式?次数分别是
多少?
第6题
7. 用语言叙述多项式“-a-3”所表示的数量关系,下列叙述正确的是
( )
A. a与-3的和 B. a的相反数与3的差
C. a的相反数与3的和 D. a的相反数与-3的差
8. 按某种标准,多项式m2-2m-1与mn+n+3属于同一类,则下列最符合
此类标准的多项式为 ( )
A. a2-b B. x2+4x+3
C. x+3y-2 D. a2b+b-1
9. 有下列各式:-34x2,2x-y,12?021x,1a3,x2y+1,-2,1π.其中,整式有
( )
A. 7个 B. 6个 C. 5个 D. 4个
?
B
B
C
10. 多项式3a2?12的常数项为________.
11. 请写出一个所含字母只有x,y,且二次项系数和常数项都是-5的三次
三项式:_______________________________.
12. 若多项式4x2y|m|-(m-1)y2+1是关于x,y的三次三项式,则m=_____.
13. (2019·大庆)用棋子摆成的“T”字形如图所示.按照图①②③的规律
摆下去,摆成第 个“T”字形需要的棋子枚数为________.
?
如x2y-5xy-5
第13题
-12
?
-1
3n+2
14. 已知关于x的多项式(a-b)x4+(b-1)x3-(a-2)x2+ax-4中不含x3项
与x2项,试写出这个多项式,并求出当x=-2时,这个多项式的值.
15. 某旅游团乘轮船出游,轮船顺流航行4小时,逆流航行2小时.已知轮船
在静水中航行的速度为x千米/时,水流的速度为y千米/时,则轮船一
共航行了多少千米?当x=30,y=10时,轮船一共航行了多少千米?
16. 礼堂有长椅x张,现有若干人在礼堂开会,若每张长椅坐5人,则有1张
长椅只坐2人,还空出6张长椅.由所提供的信息将在礼堂开会的人数用
含x的式子表示出来,指出列出的式子是单项式还是多项式,并求出当
x=70时的人数.
第1课时 用字母表示数
用字母表示数可以简明地表达问题中的数量关系,如笼子里关着5只鸡,3只兔,共有_______个头,________条腿.如果笼子里关着x只鸡,y只兔,那么共有__________个头,__________条腿.用字母表示数量关系时,要注意:(1) 在同一个问题中,相同字母所表示的量必须相同,不同字母一般表示不同的量;(2) 在同一个问题中,不同的量必须用不同的字母表示;(3) 在不同的问题中,同一个字母可以表示不同的量.
8
22
(x+y)
(2x+4y)
1. 下列含有字母的式子中,符合书写要求的是 ( )
A. ab÷2 B. ab3 C. 12xy D. 234mn
2. 七(1)班男生有a人,女生人数比男生的一半多4,则女生人数是 ( )
A. 12(a+4) B. 12(a-4) C. 12a+4 D. 12a-4
3. 列式表示:
(1) x的2倍与5的差是________;
(2) 比m的32倍大3的数是________;
(3) 小明今年m岁,小明比小丽大2岁,小丽今年_________岁;
(4) 小红家到学校的距离是1 000 m,她步行的速度是v m/min,她走了
t min还未到学校,此时她离学校的距离为_____________m.
?
C
C
2x-5
32m+3
?
(m-2)
(1 000-vt)
4. 为适应小班化教学,需要定制一批新课桌,要求一张桌面配三条桌腿.
现在工人师傅已经生产了a张桌面,则需生产________条桌腿才能正好
配套.
5. (2020·长春)长春市净月潭国家森林公园门票价格为成人票每张30元,
儿童票每张15元,若购买m张成人票和n张儿童票,则共需花费
____________元.
6. 某市出租车的收费标准:起步价为12.50元,3千米后每千米收费2.40元
(不足1千米按1千米算).某人在该市乘坐出租车行驶x千米(x>3,且x
为整数),试用含x的式子表示他应付的费用,并求当x=8时,他应付的
费用.
3a
(30m+15n)
7. 一批上衣的进价为每件a元,在进价的基础上提高50%后作为售价,现由
于季节原因,打六折促销,则打折后每件上衣的价格为 ( )
A. a元 B. 0.9a元 C. 0.92a元 D. 1.04a元
8. 已知m是两位数,n是一位数,把m直接写在n后面,就成为一个三位数,
这个三位数可表示为 ( )
A. 10n+m B. nm C. n+10m D. 100n+m
9. 某商店举办促销活动,促销的方法是将原价x元的衣服以(45x-10)元出
售,则下列说法中,能正确表达该商店促销方法的是 ( )
A. 原价减去10元后再打八折 B. 原价打八折后再减去10元
C. 原价减去10元后再打两折 D. 原价打两折后再减去10元
?
B
D
B
10. (1) 已知一个长方体的长和宽都为m,高为312,则它的体积为________.
(2) 若n表示整数,则三个连续的整数一般可写为__________________,
________,_______;三个连续的偶数一般可写为________,________,
________;三个连续的奇数一般可写为_______,________,________.
(3) 若一个两位数的十位上的数字为x,个位上的数字为y,则这个两位
数可表示为________;若把这个两位数的十位上的数字与个位上的数字
颠倒位置,则此时的两位数可表示为________.
(4) 观察下列一组数:14,39,516,725,936,…,它们是按一定的规律排
列的,那么这一组数的第n(n为正整数)个数是__________.
?
72m2
?
答案不唯一,如n
n+1
n+2
2n-2
2n
2n+2
2n-1
2n+1
2n+3
10x+y
10y+x
2n?1(n+1)2
?
11. 某书店出售图书的同时,推出一项租书业务,每租看1本书,租期不超
过3天,每天租金a元;租期超过3天,从第4天开始每天另加收b元.如
果租看1本书,租期为7天,那么租金为_________________________元.
12. 如图,用4根火柴棒可搭出1个小正方形,用7根火柴棒可搭出2个小正
方形,按照这样的方式,搭3个小正方形需用________根火柴棒,搭4
个小正方形需用________根火柴棒,搭n(n为正整数)个小正方形需用
________根火柴棒,搭100个小正方形需用________根火柴棒.
[3a+4(a+b)][或(7a+4b)]
10
13
(3n+1)
301
第12题
13. 用含字母的式子表示图中阴影部分的面积.
(1)
(2)
(3)
(1) 12ab-12mn
?
(2) ab-π(a2)2
?
(3) ab-(a-2x)(b-2x)
14. 观察下列各式:21×2=21+2;32×3=32+3;43×4=43+4;54×5=54+5;
….请你将猜想到的规律用含字母n(n为正整数)的式子表示出来.
?
第2课时 单 项 式
1. 单项式:表示数或字母的________的式子叫做单项式.特别地,单独的
一个数或一个字母也是单项式.
2. 单项式的系数:单项式中的____________叫做这个单项式的系数.
3. 单项式的次数:一个单项式中,所有字母的指数的________叫做这个单
项式的次数.对于单独一个非零的数,规定它的次数为________.
积
数字因数
和
0
1. (2020·日照)单项式-3ab的系数是 ( )
A. 3 B. -3 C. 3a D. -3a
2. 下列语句错误的是 ( )
A. 数字0也是单项式 B. 单项式-a的系数与次数都是1
C. 12xy是二次单项式 D. -2ab3的系数是-23
3. 有下列式子:-2x2,ax,1x,113x,1+a,-b,3+2a,x+y2.其中,单项
式共有 ( )
A. 2个 B. 4个 C. 6个 D. 8个
4. (2019·黄冈)-12x2y是________次单项式.
?
B
B
B
三
?
6. 下列各组单项式中,次数相同的是 ( )
A. 2ab与4xy2 B. 3π与a
C. 13x2y2与xy D. a3与xy2
7. 已知单项式-3xmy37的次数是7,则2m-17的值是 ( )
A. 8 B. -8 C. 9 D. -9
8. 已知(a-1)x2ya+1是关于x,y的五次单项式,则这个单项式的系数是
( )
A. 1 B. 2 C. 3 D. 0
?
D
D
A
9. 单项式-512xy3的系数是m,次数是n,则mn=________.
10. 若单项式-x4ymz和5a5bn都是六次单项式,则m+n=________.
11. 如果|a+2|+(b-3)2=0,那么单项式-xa+byb-a的次数是________.
12. 邮购一种书,每册书的定价为a元,另加书价的10%作为邮资.邮购这
种书n册,总计金额为y元,则y=________;当a=10.8,n=50时,y
的值为________.
13. 填表:
?
-53
?
2
6
1.1an
594
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}单项式
-15a2b
43ab2c
-0.15m
????3????47
系 数
?
?
?
?
次 数
?
?
?
?
-15
43
?
-0.15
17
?
3
4
1
7
14. 列出单项式,并指出它们的系数和次数:
(1) 某班的总人数为m,女生人数是男生人数的35,则该班的男生人数
为多少?
(2) 某班学生按横m纵n排列座次且坐满,则该班的学生人数为多少?
(3) 一辆汽车的速度为x千米/时,则该汽车行驶40分钟的路程为多少
千米?
(4) 学校购买了一批图书,共a箱,每箱有b册,将这批图书的一半捐
给社区,捐给社区的图书有多少册?
(5) 一个直角三角形的一条直角边长x cm,另一条直角边长9 cm,求
该直角三角形的面积.
?
15. 已知单项式-23xy2m-1与-22x2y2的次数相同.
(1) 求m的值;
(2) 当x=-9,y=-2时,求单项式-23xy2m-1的值.
?
16. 观察下列单项式:-x,2x2,-3x3,…,-19x19,20x20,….
(1) 根据你发现的规律,写出第101个和第102个单项式;
(2) 请写出第n(n为正整数)个单项式.
第3课时 多项式及整式
1. 多项式:几个单项式的________叫做多项式.其中,每个单项式叫做多
项式的________,不含字母的项叫做__________.
2. 多项式的次数:多项式里,次数________项的次数,叫做这个多项式的
次数.
3. 整式:________与________统称整式.
和
项
常数项
最高
单项式
多项式
1. 多项式-2a3b+3a2-4的项数及次数分别是 ( )
A. 3,3 B. 4,3
C. 3,4 D. 3,6
2. 将多项式3x2y-xy2+x3y3-x4y4-1按字母x的降幂排列,则下列各式正
确的是 ( )
A. -1-xy2+3x2y+x3y3-x4y4
B. -x4y4+x3y3+3x2y-xy2-1
C. -x4y4+x3y3-xy2+3x2y-1
D. -1+3x2y-xy2+x3y3-x4y4
C
B
3. 多项式-12x+3x2-5的次数最高项是________,一次项系数是_______,
常数项是________.
4. 小李有a2本书,小张把自己的书给了小李2a本后,他们两人书的数量相
同,则小张原来有书___________本,这是一个______次多项式.
5. 若多次项4xn+2-5x2-n+6是关于x的三次多项式,求n2-2n+3的值.
?
3x2
-12
?
-5
(a2+4a)
二
6. 小明房间的窗户如图所示,其中上方的装饰物由两个四分之一圆和一个
半圆组成(它们的半径相同).
(1) 装饰物所占的面积是多少?窗户中能射进阳光的部分的面积是多少
(窗框的面积忽略不计)?
(2) 观察(1)中所得到的结果,它们是单项式还是多项式?次数分别是
多少?
第6题
7. 用语言叙述多项式“-a-3”所表示的数量关系,下列叙述正确的是
( )
A. a与-3的和 B. a的相反数与3的差
C. a的相反数与3的和 D. a的相反数与-3的差
8. 按某种标准,多项式m2-2m-1与mn+n+3属于同一类,则下列最符合
此类标准的多项式为 ( )
A. a2-b B. x2+4x+3
C. x+3y-2 D. a2b+b-1
9. 有下列各式:-34x2,2x-y,12?021x,1a3,x2y+1,-2,1π.其中,整式有
( )
A. 7个 B. 6个 C. 5个 D. 4个
?
B
B
C
10. 多项式3a2?12的常数项为________.
11. 请写出一个所含字母只有x,y,且二次项系数和常数项都是-5的三次
三项式:_______________________________.
12. 若多项式4x2y|m|-(m-1)y2+1是关于x,y的三次三项式,则m=_____.
13. (2019·大庆)用棋子摆成的“T”字形如图所示.按照图①②③的规律
摆下去,摆成第 个“T”字形需要的棋子枚数为________.
?
如x2y-5xy-5
第13题
-12
?
-1
3n+2
14. 已知关于x的多项式(a-b)x4+(b-1)x3-(a-2)x2+ax-4中不含x3项
与x2项,试写出这个多项式,并求出当x=-2时,这个多项式的值.
15. 某旅游团乘轮船出游,轮船顺流航行4小时,逆流航行2小时.已知轮船
在静水中航行的速度为x千米/时,水流的速度为y千米/时,则轮船一
共航行了多少千米?当x=30,y=10时,轮船一共航行了多少千米?
16. 礼堂有长椅x张,现有若干人在礼堂开会,若每张长椅坐5人,则有1张
长椅只坐2人,还空出6张长椅.由所提供的信息将在礼堂开会的人数用
含x的式子表示出来,指出列出的式子是单项式还是多项式,并求出当
x=70时的人数.
