广东省东莞市2020-2021学年高二下学期期末考试数学试题 Word版含答案
文档属性
| 名称 | 广东省东莞市2020-2021学年高二下学期期末考试数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 569.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-09 09:47:09 | ||
图片预览




文档简介
东莞市2020-2021学年度第二学期教学质量检查
高二数学
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题給出的四个选项中,只有一项是符合题目要求的.请把正确选项在答题卡中的相应位置涂黑.
1.已知函数false,则false( )
A.false B.false C.false D.false
2.设随机变量x服从正态分布false,若false,则false( )
A.1 B.2 C.3 D.4
3.A,B,C,D,E等5名学生进入学校劳动技能大赛决赛,并决出第一至第五名的名次(无并列名次).已知学生A和B都不是第一名也都不是最后一名,则这5人最终名次的不同排列有( )
A.18种 B.36种 C.48种 D.54种
4.某企业建立了风险分级管控和隐患排查治理的双重独立预防机制,已知两套机制失效的概率分别为false和false,则恰有一套机制失效的概率为( )
A.false B.false C.false D.false
5.我国古代典籍《周易》用“卦”描述万物的变化,毎一卦由六爻组成.有一种“金钱起卦法”,其做法为:取两枚相同的钱币合于双手中,上下摇动数下,再撒钱币到桌面或平盘等硬物上,此为一爻,重复六次,得到六爻.两枚钱币全部正面向上称为变爻,若每一枚钱币正面向上的概率为false,则一卦中恰有两个变爻的概率为( )
A.false B.false C.false D.false
6.false展开式中的常数项为( )
A.-40 B.-20 C.20 D.40
7.某放射性同位素在衰变过程中,其含量N(单位:贝克)与时间t(单位:天)满足函数关系false,其中false为false时该同位素的含量.已知false时,该同位素含量的时变化率为false,则false( )
A.24贝克 B.false贝克 C.1贝克 D.false贝克
8.已知函数false,false,若存在实数false,false使得false,则false的最大值为( )
A.false B.1 C.false D.false
二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分.请把正确选项在答题卡中的相应位置涂黑
9.下列结论正确的是( )
A.若两个具有线性相关关系的变量的相关性越强,则相关系数false的绝对值false越接近于1
B.样本false的回归直线false至少经过其中一个样本点
C.在回归方程false中,当解释变量x每增加1个单位时,预报变量false平均增加0.2个单位
D.在线性回归模型中,用相关指数false刻画拟合效果,false的值越小,模型的拟合效果越好
10.已知复数z满足false,则false的可能取值有( )
A.0 B.1 C.2 D.3
11.图1是函数false的导函数false的图象,则下列结论正确的是( )
A.false B.false是false的极小值点
C.false是false的极小值点 D.false是false的极大值点
12.将3个不同的小球随机放入4个不同的盒子,用false表示空盒子的个数,则下列结论正确的是( )
A.false B.false C.false D.false
三、填空题:本大题共4小题,每小题5分,共20分.请把答案填在答题卡的相应位置上.
13.在两名男生与三名女生中随机抽取两人进行某项体能测试,则在第1次抽到男生的条件下,第2次抽到女生的概率为_________________.
14.若复数false(i是虚数单位)是纯虚数,则实数false______________.
15.已知图2是“杨辉三角”,图3是“莱布尼茨三角”,两个“三角”之间具有关联性.已知“杨辉三角”中第n行第false个数为false,则“莱布尼茨三角”中第n行第false个数为______________;已知“杨辉三角”中第n行和第false行中的数满足关系式false,类比写出“莱布尼茨三角”中第n行和第false行中的数满足的关系式________________.
16.若false与false的图象有且仅有两个公共点,则实数a的取值范围为_____________.
四、解答题:本大题共6小题,第17题10分,18、19、20、21、22题各12分,共70分.解答应写岀文字说明、证明过程或演算步骤.必须把解答过程写在答题卡相应题号指定的区域内,超出指定区域的答案无效.
17.(本小题满分10分)
已知函数false.
(1)求函数false的极值;
(2)若对任意的false都有false成立,求c的取值范围.
18.(本小题满分12分)
已知复数false,false.
(1)当false,false,false,false时,求false,false,false;
(2)根据(1)的计算结果猜想false与false的关系,并证明该关系的一般性;
(3)结合(2)的结论进行类比或推广,写出一个复数的模的运算性质(不用证明).
19.(本小题满分12分)
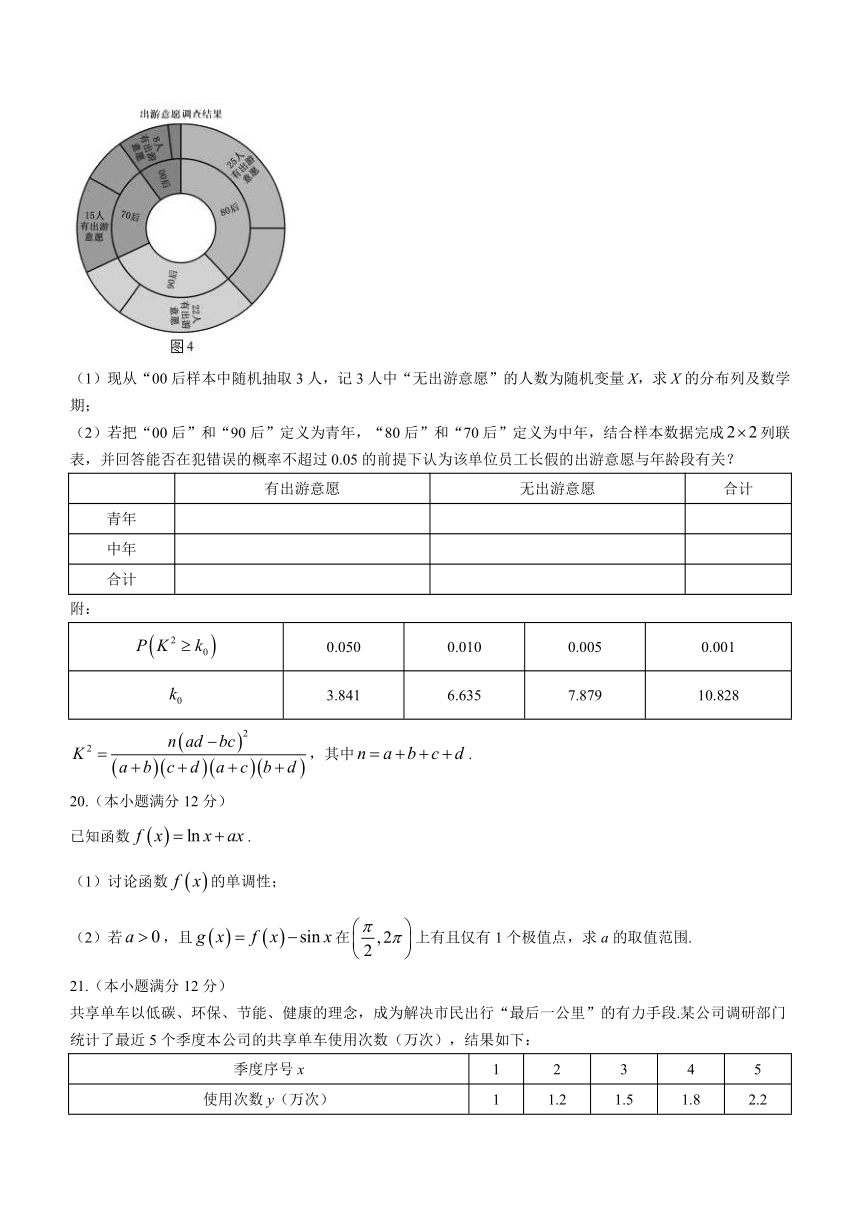
为了了解员工长假的出游意愿,某单位从“70后”至“00后”的人群中按年龄段分层抽取了100名员工进行调查.调查结果如图4所示,已知每个员工仅有“有出游意愿”和“无出游意愿”两种回答,且样本中“00后”与“90后”员工占比分别为10%和30%.
(1)现从“00后样本中随机抽取3人,记3人中“无出游意愿”的人数为随机变量X,求X的分布列及数学期;
(2)若把“00后”和“90后”定义为青年,“80后”和“70后”定义为中年,结合样本数据完成false列联表,并回答能否在犯错误的概率不超过0.05的前提下认为该单位员工长假的出游意愿与年龄段有关?
有出游意愿
无出游意愿
合计
青年
中年
合计
附:
false
0.050
0.010
0.005
0.001
false
3.841
6.635
7.879
10.828
false,其中false.
20.(本小题满分12分)
已知函数false.
(1)讨论函数false的单调性;
(2)若false,且false在false上有且仅有1个极值点,求a的取值范围.
21.(本小题满分12分)
共享单车以低碳、环保、节能、健康的理念,成为解决市民出行“最后一公里”的有力手段.某公司调研部门统计了最近5个季度本公司的共享单车使用次数(万次),结果如下:
季度序号x
1
2
3
4
5
使用次数y(万次)
1
1.2
1.5
1.8
2.2
(1)(i)根据上表,画岀散点图并根据所画散点图,判断能否用线性回归模型拟合使用次数y与季度序号x之间的关系,如果能,求出y关于x的线性回归方程;如果不能,请说明理由.
(ii)如果你是公司主管领导,你会在下一季度向市场增加投放共享单车吗?请说明理由.
(2)为进一步开拓市场做准备,公司目前接受报价的有两款车型:A型单车每辆500元,第一年收入500元,以后逐年递减80元;B型单车每辆300元,第一年收入500元,以后逐年递减100元.经市场调研,两款车型使用寿命频数统计如下表:
车型\使用寿命
1年
2年
3年
4年
总计
A
10
20
30
40
100
B
10
35
30
25
100
不考虑除釆购成本以外的其它成本,假设毎辆单车的使用寿命都是整数年,用频率估计概率,以1辆单车所产生的利润的数学期望为决策依据,如果你是公司负责人,会选择哪款车型?
参考数据:false,false.
参考公式:false,false.
22.(本小题满分12分)
已知函数false,false.
(1)证明false恒成立;
(2)用false表示m,n中的最大值.已知函数false,记函数false,若函数false在false上恰有2个零点,求实数a的取值范围.
东莞市2020-2021学年度第二学期教学质量检查
高二数学参考答案
一、单项选择题
题号
1
2
3
4
5
6
7
8
答案
D
C
B
C
A
D
B
B
二、多项选择题(全部选对的得5分,选对但不全的得2分,有选错的得0分)
题号
9
10
11
12
答案
AC
BC
CD
AD
三、填空题(15题第一空2分,第二空3分)
13.false 14.1 15.false;false
16.false
四、解答题
17.解:(1)因为false,所以false,.…………………………1分
令false,解得false或false,
当false,即false或false;当false,即false,.………………………………3分
故false的单调递增区间为false和false,单调递减区间为false,.………………4分
所以,false时,false有极大值false,.………………………………………………5分
当false时,false有极小值false.……………………………………………………6分
(2)由(1)知false在false上单调递减,在false上单调递增,.…………………………7分
又false,false,.…………………………………………………………………………8分
所以false时,false,.……………………………………………………………………9分
因为对任意的false都有false成立,所以false.………………………………………………10分
18.解(1)由题知false,false,.……………………………………2分
false,.…………………………………………………………3分
所以false.………………………………………………………………4分
(2)猜想false,.………………………………………………………………5分
证明:因为false,false,.………………………………………………6分
所以false,.…………………………7分
因为false,.……………………………………8分
所以false.…………………………9分
所以false成立.…………………………………………………………………………10分
(3)false,或false,或false.
说明:只要写出复数模运算相关的一个正确结论即可给2分.…………………………………………12分
19.解:(1)由题知,样本中“00后”员工人数false人,.…………………………1分
由图4知,其中8人有出游意愿,2人无出游意愿,
从中随机抽取3人,抽到“无出游意愿”的人数X的所有可能取值为0,1,2,.……………………2分
false,false,false,
随机变量X的分布列为
X
0
1
2
P
false
false
false
.………………………………………………………………………………………………………………5分
随机变量X的期望false.………………………………………………6分
(2)由题知,样本中中年员工占比为false,人数false人,青年员工人数false人,.………………………………………………………………………………7分
结合图3得到如下false列联表,
有出游意愿
无出游意愿
合计
青年
30
10
40
中年
40
20
60
合计
70
30
100
.…………………………………………………………………………………………………………9分
假设“有岀游意愿与年龄段无关”,则
false,.……………………………………………11分
∴不能在犯错误的概率不超过0.05的前提下认为该单位员工长假的出游意愿与年龄段有关.………………12分
20.解:(1)由题得,函数定义域为false,false,.……………………………………1分
①当false时,false在false上恒成立,
所以函数false在false上单调递增;.………………………………………………………………3分
②当false时,由false,得false,
当false时,false;当false时,false,
所以false在false上单调递增,在false上单调递减,.……………………………………5分
综上所述,当false时,false在false上单调递增;
当false时,false在false上单调递增,在false上单调递减.………………………………6分
(2)由题得false,令false,得false,.……………………7分
因为false在false上有且仅有1个极值点,
所以false与false在false的图象有且仅有一个交点,.…………………………8分
①当false时,false,此时false与false没有交点,.……………………9分
②当false时,由前面的分析得,两个函数图象在false上有且仅有一个交点,则false,即false,.……………………………………………………11分
综上所述,a的取值范围为false.…………………………………………………………12分
21.解:(1)(i)散点图如图所示:
根据散点图,可以用线性回归模型拟合使用次数y与次季度序号x之间的关系,
设回归方程为false,
则false,
由false,false,得false,
所以y关于x的线性回归方程为false.
(ii)开放型答案,根据学生理由叙述情况,酌情给分.
参考答案一:下一季度可以向市场增加投放共享单车,理由:
①由(i)中散点图判断可预估下季度市场对本公司单车使用次数会持续上涨;
②由(i)中使用次数y关于季度序号x的线性回归方程false可知,下季度市场对本公司单车下一季度的使用次数会持续上涨0.3万次左右,因此需要向市场增加投放共享单车.
说明:答岀一种理由即可给满1分,其他理由酌情给分.………………………………………………5分
参考答案二:下一季度可以先不向市场增加投放共享单车,理由:
题中只给岀了使用次数这一方面的数据,是否增加投放共享单车还要考察单车的使用率高低,单车的区域分布是否合理,单车使用后的回收与分配是否及时等等因素,这些都会影响投放单车的决策,因此要进行进一步调查过后才能决定.
说明:答岀一种理由即可给满1分,其他理由酌情给分.……………………………………………………5分
(2)设1辆A型单车产生的毛利润为随机变量false,则false的所有可能取值为500,920,1260,1520,.…….……………………………………………………………………………………6分
用频率估计概率,则1辆A型单车产生毛利润的分布列为
毛利润false
500
920
1260
1520
概率false
false
false
false
false
.………………………………………………………………………………………………………………7分
则1辆A型单车毛利润的数学期望false,故1辆A型单车纯利润的数字期望为false,.………………………………………………………………8分
设1辆B型单车产生的毛利润为随机变量false,则false的所有可能取值为500,900,1200,1400,.……9分
用频率估计概率,则1辆B型单车产生毛利润的分布列为
毛利润false
500
900
1200
1400
概率false
false
false
false
false
.………………………………………………………………………………………………………………10分
则1辆B型单车毛利润的数学期望false,故1辆B型单车纯利润的数学期望为false,.…………………………………………………………11分
因为1辆B型单车纯利润的数学期望大于1辆A型单车的,所以选择B型单车.……………………分
22.解:(1)由题得false的定义域为false,
则false在false上恒成立等价于false在false上恒成立,.……1分
记false,则false,.……………………………………………………2分
当false时,false;false时,false,
故false在false上单调递减,false上单调递增,.……………………………………………………3分
所以false,即false恒成立.………………………………………………………………4分
(2)由题得false,
①当false时,false,此时无零点.……………………………………………………5分
②当false时,false,false
a.当false,即false时,false是false的一个零点;
b.当false,即false时,false不是false的一个零点;.…………………………6分
③当false时,false恒成立,因此只需考虑false在false上的零点情况.
由false
a.当false时,false,false在false上单调递增,且false,
当false时,false,则false在false上无零点,故false在false上无零点;
当false时,false,则false在false上无零点,故false在false上有1个零点;
当false时,由false,false,得false在false上仅有一个零点,故false在false上有2个零点;
所以false,.…………………………………………………………………………9分
b.当false时,由false得false,
由false时,false;当false时false,false,
故false在false上单调递减,false在false上单调递增;
由false,false,得false在false上仅有一个零点,故false在false上有2个零点;
所以false,.…………………………………………………………………………………………11分
综上所述,false时,false在false上恰有两个零点.………………………………………………12分
高二数学
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题給出的四个选项中,只有一项是符合题目要求的.请把正确选项在答题卡中的相应位置涂黑.
1.已知函数false,则false( )
A.false B.false C.false D.false
2.设随机变量x服从正态分布false,若false,则false( )
A.1 B.2 C.3 D.4
3.A,B,C,D,E等5名学生进入学校劳动技能大赛决赛,并决出第一至第五名的名次(无并列名次).已知学生A和B都不是第一名也都不是最后一名,则这5人最终名次的不同排列有( )
A.18种 B.36种 C.48种 D.54种
4.某企业建立了风险分级管控和隐患排查治理的双重独立预防机制,已知两套机制失效的概率分别为false和false,则恰有一套机制失效的概率为( )
A.false B.false C.false D.false
5.我国古代典籍《周易》用“卦”描述万物的变化,毎一卦由六爻组成.有一种“金钱起卦法”,其做法为:取两枚相同的钱币合于双手中,上下摇动数下,再撒钱币到桌面或平盘等硬物上,此为一爻,重复六次,得到六爻.两枚钱币全部正面向上称为变爻,若每一枚钱币正面向上的概率为false,则一卦中恰有两个变爻的概率为( )
A.false B.false C.false D.false
6.false展开式中的常数项为( )
A.-40 B.-20 C.20 D.40
7.某放射性同位素在衰变过程中,其含量N(单位:贝克)与时间t(单位:天)满足函数关系false,其中false为false时该同位素的含量.已知false时,该同位素含量的时变化率为false,则false( )
A.24贝克 B.false贝克 C.1贝克 D.false贝克
8.已知函数false,false,若存在实数false,false使得false,则false的最大值为( )
A.false B.1 C.false D.false
二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分.请把正确选项在答题卡中的相应位置涂黑
9.下列结论正确的是( )
A.若两个具有线性相关关系的变量的相关性越强,则相关系数false的绝对值false越接近于1
B.样本false的回归直线false至少经过其中一个样本点
C.在回归方程false中,当解释变量x每增加1个单位时,预报变量false平均增加0.2个单位
D.在线性回归模型中,用相关指数false刻画拟合效果,false的值越小,模型的拟合效果越好
10.已知复数z满足false,则false的可能取值有( )
A.0 B.1 C.2 D.3
11.图1是函数false的导函数false的图象,则下列结论正确的是( )
A.false B.false是false的极小值点
C.false是false的极小值点 D.false是false的极大值点
12.将3个不同的小球随机放入4个不同的盒子,用false表示空盒子的个数,则下列结论正确的是( )
A.false B.false C.false D.false
三、填空题:本大题共4小题,每小题5分,共20分.请把答案填在答题卡的相应位置上.
13.在两名男生与三名女生中随机抽取两人进行某项体能测试,则在第1次抽到男生的条件下,第2次抽到女生的概率为_________________.
14.若复数false(i是虚数单位)是纯虚数,则实数false______________.
15.已知图2是“杨辉三角”,图3是“莱布尼茨三角”,两个“三角”之间具有关联性.已知“杨辉三角”中第n行第false个数为false,则“莱布尼茨三角”中第n行第false个数为______________;已知“杨辉三角”中第n行和第false行中的数满足关系式false,类比写出“莱布尼茨三角”中第n行和第false行中的数满足的关系式________________.
16.若false与false的图象有且仅有两个公共点,则实数a的取值范围为_____________.
四、解答题:本大题共6小题,第17题10分,18、19、20、21、22题各12分,共70分.解答应写岀文字说明、证明过程或演算步骤.必须把解答过程写在答题卡相应题号指定的区域内,超出指定区域的答案无效.
17.(本小题满分10分)
已知函数false.
(1)求函数false的极值;
(2)若对任意的false都有false成立,求c的取值范围.
18.(本小题满分12分)
已知复数false,false.
(1)当false,false,false,false时,求false,false,false;
(2)根据(1)的计算结果猜想false与false的关系,并证明该关系的一般性;
(3)结合(2)的结论进行类比或推广,写出一个复数的模的运算性质(不用证明).
19.(本小题满分12分)
为了了解员工长假的出游意愿,某单位从“70后”至“00后”的人群中按年龄段分层抽取了100名员工进行调查.调查结果如图4所示,已知每个员工仅有“有出游意愿”和“无出游意愿”两种回答,且样本中“00后”与“90后”员工占比分别为10%和30%.
(1)现从“00后样本中随机抽取3人,记3人中“无出游意愿”的人数为随机变量X,求X的分布列及数学期;
(2)若把“00后”和“90后”定义为青年,“80后”和“70后”定义为中年,结合样本数据完成false列联表,并回答能否在犯错误的概率不超过0.05的前提下认为该单位员工长假的出游意愿与年龄段有关?
有出游意愿
无出游意愿
合计
青年
中年
合计
附:
false
0.050
0.010
0.005
0.001
false
3.841
6.635
7.879
10.828
false,其中false.
20.(本小题满分12分)
已知函数false.
(1)讨论函数false的单调性;
(2)若false,且false在false上有且仅有1个极值点,求a的取值范围.
21.(本小题满分12分)
共享单车以低碳、环保、节能、健康的理念,成为解决市民出行“最后一公里”的有力手段.某公司调研部门统计了最近5个季度本公司的共享单车使用次数(万次),结果如下:
季度序号x
1
2
3
4
5
使用次数y(万次)
1
1.2
1.5
1.8
2.2
(1)(i)根据上表,画岀散点图并根据所画散点图,判断能否用线性回归模型拟合使用次数y与季度序号x之间的关系,如果能,求出y关于x的线性回归方程;如果不能,请说明理由.
(ii)如果你是公司主管领导,你会在下一季度向市场增加投放共享单车吗?请说明理由.
(2)为进一步开拓市场做准备,公司目前接受报价的有两款车型:A型单车每辆500元,第一年收入500元,以后逐年递减80元;B型单车每辆300元,第一年收入500元,以后逐年递减100元.经市场调研,两款车型使用寿命频数统计如下表:
车型\使用寿命
1年
2年
3年
4年
总计
A
10
20
30
40
100
B
10
35
30
25
100
不考虑除釆购成本以外的其它成本,假设毎辆单车的使用寿命都是整数年,用频率估计概率,以1辆单车所产生的利润的数学期望为决策依据,如果你是公司负责人,会选择哪款车型?
参考数据:false,false.
参考公式:false,false.
22.(本小题满分12分)
已知函数false,false.
(1)证明false恒成立;
(2)用false表示m,n中的最大值.已知函数false,记函数false,若函数false在false上恰有2个零点,求实数a的取值范围.
东莞市2020-2021学年度第二学期教学质量检查
高二数学参考答案
一、单项选择题
题号
1
2
3
4
5
6
7
8
答案
D
C
B
C
A
D
B
B
二、多项选择题(全部选对的得5分,选对但不全的得2分,有选错的得0分)
题号
9
10
11
12
答案
AC
BC
CD
AD
三、填空题(15题第一空2分,第二空3分)
13.false 14.1 15.false;false
16.false
四、解答题
17.解:(1)因为false,所以false,.…………………………1分
令false,解得false或false,
当false,即false或false;当false,即false,.………………………………3分
故false的单调递增区间为false和false,单调递减区间为false,.………………4分
所以,false时,false有极大值false,.………………………………………………5分
当false时,false有极小值false.……………………………………………………6分
(2)由(1)知false在false上单调递减,在false上单调递增,.…………………………7分
又false,false,.…………………………………………………………………………8分
所以false时,false,.……………………………………………………………………9分
因为对任意的false都有false成立,所以false.………………………………………………10分
18.解(1)由题知false,false,.……………………………………2分
false,.…………………………………………………………3分
所以false.………………………………………………………………4分
(2)猜想false,.………………………………………………………………5分
证明:因为false,false,.………………………………………………6分
所以false,.…………………………7分
因为false,.……………………………………8分
所以false.…………………………9分
所以false成立.…………………………………………………………………………10分
(3)false,或false,或false.
说明:只要写出复数模运算相关的一个正确结论即可给2分.…………………………………………12分
19.解:(1)由题知,样本中“00后”员工人数false人,.…………………………1分
由图4知,其中8人有出游意愿,2人无出游意愿,
从中随机抽取3人,抽到“无出游意愿”的人数X的所有可能取值为0,1,2,.……………………2分
false,false,false,
随机变量X的分布列为
X
0
1
2
P
false
false
false
.………………………………………………………………………………………………………………5分
随机变量X的期望false.………………………………………………6分
(2)由题知,样本中中年员工占比为false,人数false人,青年员工人数false人,.………………………………………………………………………………7分
结合图3得到如下false列联表,
有出游意愿
无出游意愿
合计
青年
30
10
40
中年
40
20
60
合计
70
30
100
.…………………………………………………………………………………………………………9分
假设“有岀游意愿与年龄段无关”,则
false,.……………………………………………11分
∴不能在犯错误的概率不超过0.05的前提下认为该单位员工长假的出游意愿与年龄段有关.………………12分
20.解:(1)由题得,函数定义域为false,false,.……………………………………1分
①当false时,false在false上恒成立,
所以函数false在false上单调递增;.………………………………………………………………3分
②当false时,由false,得false,
当false时,false;当false时,false,
所以false在false上单调递增,在false上单调递减,.……………………………………5分
综上所述,当false时,false在false上单调递增;
当false时,false在false上单调递增,在false上单调递减.………………………………6分
(2)由题得false,令false,得false,.……………………7分
因为false在false上有且仅有1个极值点,
所以false与false在false的图象有且仅有一个交点,.…………………………8分
①当false时,false,此时false与false没有交点,.……………………9分
②当false时,由前面的分析得,两个函数图象在false上有且仅有一个交点,则false,即false,.……………………………………………………11分
综上所述,a的取值范围为false.…………………………………………………………12分
21.解:(1)(i)散点图如图所示:
根据散点图,可以用线性回归模型拟合使用次数y与次季度序号x之间的关系,
设回归方程为false,
则false,
由false,false,得false,
所以y关于x的线性回归方程为false.
(ii)开放型答案,根据学生理由叙述情况,酌情给分.
参考答案一:下一季度可以向市场增加投放共享单车,理由:
①由(i)中散点图判断可预估下季度市场对本公司单车使用次数会持续上涨;
②由(i)中使用次数y关于季度序号x的线性回归方程false可知,下季度市场对本公司单车下一季度的使用次数会持续上涨0.3万次左右,因此需要向市场增加投放共享单车.
说明:答岀一种理由即可给满1分,其他理由酌情给分.………………………………………………5分
参考答案二:下一季度可以先不向市场增加投放共享单车,理由:
题中只给岀了使用次数这一方面的数据,是否增加投放共享单车还要考察单车的使用率高低,单车的区域分布是否合理,单车使用后的回收与分配是否及时等等因素,这些都会影响投放单车的决策,因此要进行进一步调查过后才能决定.
说明:答岀一种理由即可给满1分,其他理由酌情给分.……………………………………………………5分
(2)设1辆A型单车产生的毛利润为随机变量false,则false的所有可能取值为500,920,1260,1520,.…….……………………………………………………………………………………6分
用频率估计概率,则1辆A型单车产生毛利润的分布列为
毛利润false
500
920
1260
1520
概率false
false
false
false
false
.………………………………………………………………………………………………………………7分
则1辆A型单车毛利润的数学期望false,故1辆A型单车纯利润的数字期望为false,.………………………………………………………………8分
设1辆B型单车产生的毛利润为随机变量false,则false的所有可能取值为500,900,1200,1400,.……9分
用频率估计概率,则1辆B型单车产生毛利润的分布列为
毛利润false
500
900
1200
1400
概率false
false
false
false
false
.………………………………………………………………………………………………………………10分
则1辆B型单车毛利润的数学期望false,故1辆B型单车纯利润的数学期望为false,.…………………………………………………………11分
因为1辆B型单车纯利润的数学期望大于1辆A型单车的,所以选择B型单车.……………………分
22.解:(1)由题得false的定义域为false,
则false在false上恒成立等价于false在false上恒成立,.……1分
记false,则false,.……………………………………………………2分
当false时,false;false时,false,
故false在false上单调递减,false上单调递增,.……………………………………………………3分
所以false,即false恒成立.………………………………………………………………4分
(2)由题得false,
①当false时,false,此时无零点.……………………………………………………5分
②当false时,false,false
a.当false,即false时,false是false的一个零点;
b.当false,即false时,false不是false的一个零点;.…………………………6分
③当false时,false恒成立,因此只需考虑false在false上的零点情况.
由false
a.当false时,false,false在false上单调递增,且false,
当false时,false,则false在false上无零点,故false在false上无零点;
当false时,false,则false在false上无零点,故false在false上有1个零点;
当false时,由false,false,得false在false上仅有一个零点,故false在false上有2个零点;
所以false,.…………………………………………………………………………9分
b.当false时,由false得false,
由false时,false;当false时false,false,
故false在false上单调递减,false在false上单调递增;
由false,false,得false在false上仅有一个零点,故false在false上有2个零点;
所以false,.…………………………………………………………………………………………11分
综上所述,false时,false在false上恰有两个零点.………………………………………………12分
同课章节目录
