广东省梅州市2020-2021学年高一下学期期末考试数学试题 Word版含答案
文档属性
| 名称 | 广东省梅州市2020-2021学年高一下学期期末考试数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-09 09:52:41 | ||
图片预览



文档简介
梅州市高中期末考试试卷(2021.7)
高一数学
注意事项:
本试卷共6页,22小题,满分150分.考试用时120分钟.
1. 答卷前,考生务必用黑色字迹钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上.
2. 选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上.
3. 作答必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液..不按以上要求作答的答案无效.
4. 考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回.
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求.
1. 设复数false(false是虚数单位),则false( )
A. false B. false C. false D. false
2. 一水平放置的平面图形,用斜二测画法画出了它的直观图,此直观图恰好是一个边长为2的正方形,则原平面图形的面积为( )
A. false B. false C. false D. false
3. 设false、false为两个互斥事件,且false,false,则下列各式错误的是( )
A. false B. false
C. false D. false
4. 已知false,false是两个不同的平面,false,false是两条不同的直线,则下列结论正确的是( )
A. 若false,false,false,则false B. 若false,false,false,则false
C. 若false,false,则false D. 若false,false,false,则false
5. 已知平面向量false,false,false与false垂直,则false的值是( )
A. -1 B. 1 C. -2 D. 2
6. 已知一组样本数据false,false,false,…,false,且false,平均数false,则该组数据的方差false( )
A. 1 B. false C. 2 D. false
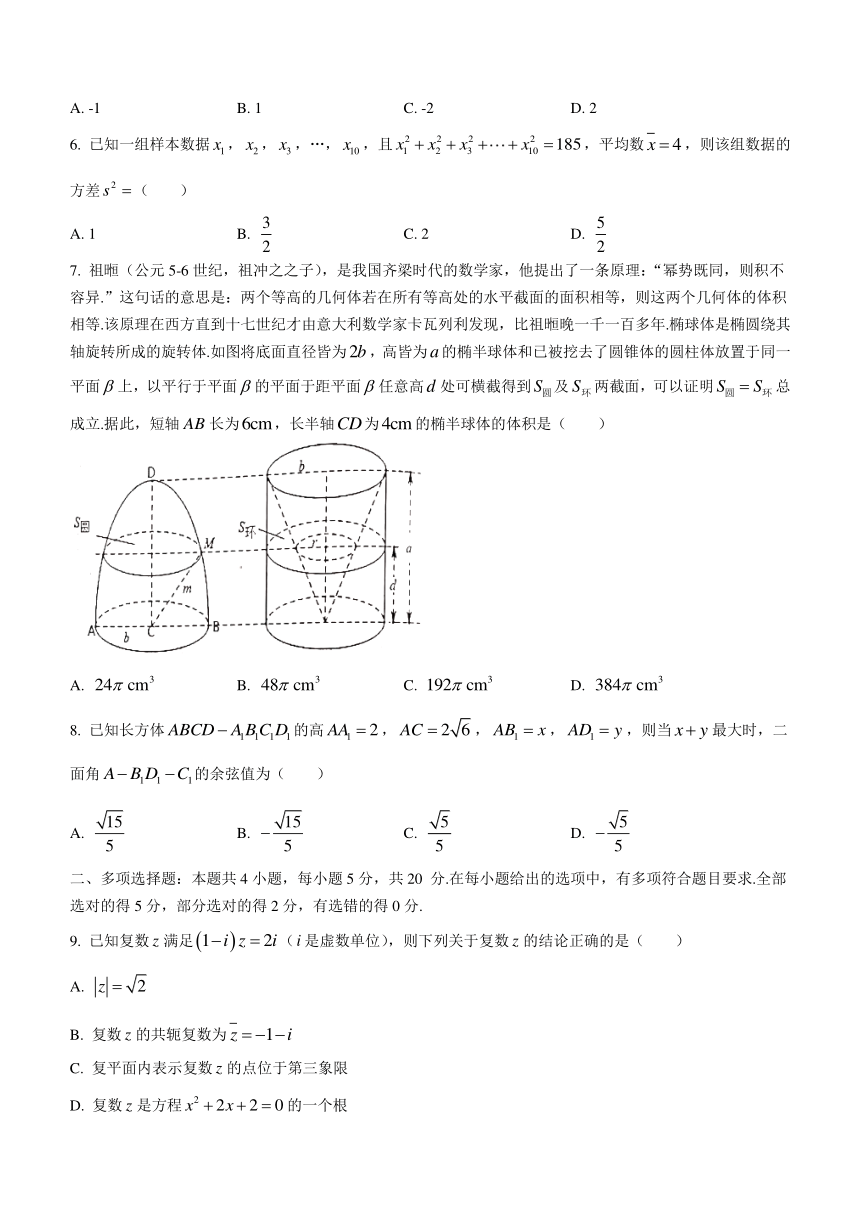
7. 祖暅(公元5-6世纪,祖冲之之子),是我国齐梁时代的数学家,他提出了一条原理:“幂势既同,则积不容异.”这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现,比祖暅晚一千一百多年.椭球体是椭圆绕其轴旋转所成的旋转体.如图将底面直径皆为false,高皆为false的椭半球体和已被挖去了圆锥体的圆柱体放置于同一平面false上,以平行于平面false的平面于距平面false任意高false处可横截得到false及false两截面,可以证明false总成立.据此,短轴false长为false,长半轴false为false的椭半球体的体积是( )
A. false B. false C. false D. false
8. 已知长方体false的高false,false,false,false,则当false最大时,二面角false的余弦值为( )
A. false B. false C. false D. false
二、多项选择题:本题共4小题,每小题5分,共20 分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 已知复数false满足false(false是虚数单位),则下列关于复数false的结论正确的是( )
A. false
B. 复数false的共轭复数为false
C. 复平面内表示复数false的点位于第三象限
D. 复数false是方程false的一个根
10. 已知false的内角false,false,false所对边的长分别为false,false,false,false,false,false,若满足条件的false有两个,则false的值可以是( )
A. false B. false C. 3 D. 4
11. 在疫情防护知识竞赛中,对某校2000名考生的参赛成绩进行统计,可得到如图所示的频率分布直方图,其中分组的区间为false,false,false,false,false,false,60分以下视为不及格,若同一组中数据用该组区间中间值作代表值,则下列说法中正确的是( )
A. 成绩在false的考生人数最多
B. 不及格的考生人数为500
C. 考生竞赛成绩的众数为75分
D. 考生竞赛成绩的中位数约为75分
12. 正方体false中,false是棱false的中点,false在侧面false上运动,且满足false平面false.以下命题正确的有( )
A. 侧面false上存在点false,使得false
B. 直线false与直线false所成角可能为false
C. 平面false与平面false所成锐二面角的正切值为false
D. 设正方体棱长为1,则过点false,false,false的平面截正方体所得的截面面积的最大值为false
三、填空题:本题共4小题,每题5分,共 20分.
13. 向量false,false满足false,false,false与false的夹角为false,则false__________.
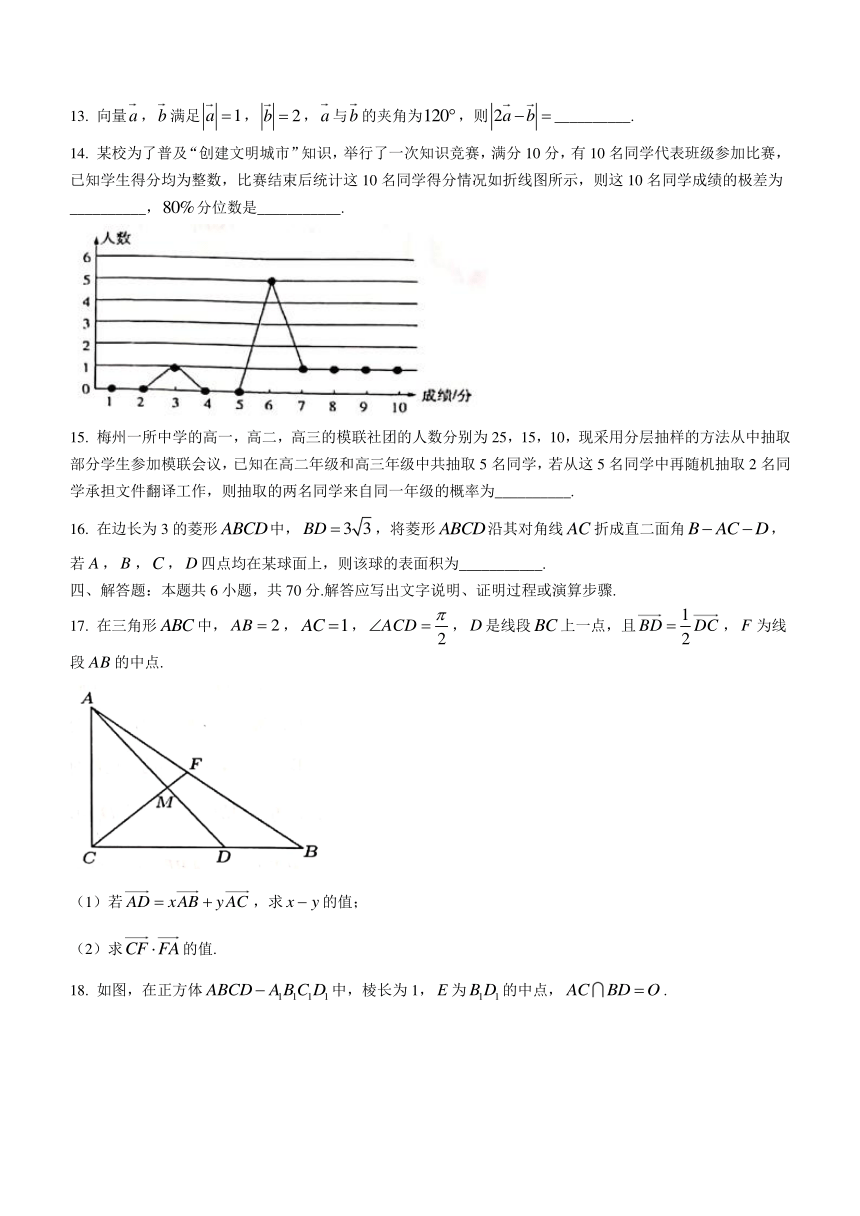
14. 某校为了普及“创建文明城市”知识,举行了一次知识竞赛,满分10分,有10名同学代表班级参加比赛,已知学生得分均为整数,比赛结束后统计这10名同学得分情况如折线图所示,则这10名同学成绩的极差为__________,false分位数是___________.
15. 梅州一所中学的高一,高二,高三的模联社团的人数分别为25,15,10,现采用分层抽样的方法从中抽取部分学生参加模联会议,已知在高二年级和高三年级中共抽取5名同学,若从这5名同学中再随机抽取2名同学承担文件翻译工作,则抽取的两名同学来自同一年级的概率为__________.
16. 在边长为3的菱形false中,false,将菱形false沿其对角线false折成直二面角false,若false,false,false,false四点均在某球面上,则该球的表面积为___________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17. 在三角形false中,false,false,false,false是线段false上一点,且false,false为线段false的中点.
(1)若false,求false的值;
(2)求false的值.
18. 如图,在正方体false中,棱长为1,false为false的中点,false.
(1)求证:false平面false;
(2)求证:false平面false;
(3)求三棱锥false的体积.
19. 在①false;②false;③false这三个条件中任选一个,补充在下面问题中,然后解答补充完整的题目.
在false中,内角false,false,false的对边分别为false,false,false,且____________________.
(1)求角false;
(2)若false,false的面积为false,求false的周长.
(注:如果选择多个条件分别解答,按第一个解答计分)
20. 我市某校为了解高一新生对文理科的选择,对1000名高一新生发放文理科选择调查表,统计知,有600名学生选择理科,400名学生选择文科.分别从选择理科和文科的学生中随机各抽取20名学生的数学成绩得如下累计表:
分数段
理科人数
文科人数
false
false
false
false
false
false
(1)利用统计表数据分析:选择文理科学生的数学平均分及数学成绩对学生选择文理科的影响;并绘制选择理科的学生的数学成绩的频率分布直方图;
(2)从数学成绩不低于70分的选择理科和文科的学生中各取一名学生的数学成绩,求选取理科学生的数学成绩至少高于选取文科学生的数学成绩一个分数段的概率.
21. 如图,在三棱柱false中,平面false底面false,false,false,false,false,false为false的中点,侧棱false.
(1)求证:false;
(2)求直线false与平面false所成角的余弦值.
22. 芹洋湿地公园是以水为主题的公园,以湿地良好生态环境和多样化湿地景观资源为基础的生态型主题公园.欲在该公园内搭建一个形状为平面凸四边形false的休闲、观光及科普宣教的平台,如图所示,其中false(单位:百米),false(单位:百米),false为正三角形.建成后false将作为人们旅游观光、休闲娱乐的区域,false将作为科普宣教湿地功能利用、弘扬湿地文化的区域.
(1)当false时,求旅游观光、休闲娱乐的区域false的面积;
(2)求旅游观光、休闲娱乐的区域false面积的最大值.
梅州市高中期末考试试卷(2021.7)
高一数学参考答案与评分意见
一、单项选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1-5:CABDA 6-8:DAB
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9. ABD 10. BC 11. AC 12. AC
三、填空题:本大题共4小题,每小题5分,满分20分.
13. false 14. 7,8.5 15. false 16. false
四、解答题:本大题共6小题,满分70分.解答须写出文字说明,证明过程或演算步骤.
17. 解:(1)∵false,∴false,
得false,
∵false,∴false,false,
∴false.
(2)∵在三角形false中,false,false,false,
∴false,false,
∵false,∴false为等边三角形,
∴false.
18.(1)证明:∵在正方体中,false平面false,
false平面false,∴false,
∵false,false,
∴false平面false.
(2)证明:连接false,
∵在正方体中,false且false,
∴四边形false是平行四边形,
∴false且false,
∵false,false分别为false,false中点,∴false,
∴四边形false是平行四边形,
∴false,
∵false平面false,false平面false,
∴false平面false.
(3)由(2)得false平面false,
∴false点到平面false的距离即为false点到平面false的距离,
∴false
false
false.
19. 解:(1)选①,∵false,
∴由正弦定理得false,
即false,
又在false中,false,false,false,
∴false,
∴false,
∵false,
∴false.
选②,∵false,
∴由正弦定理得false,
又在false中,false,false,
∴false,
∵false,
∴false.
选③,∵false,
∴false,即false,
∴由余弦定理得false,
∵false,
∴false.
(2)∵false,false,false的面积为false,
∴false,
∴false,
又由余弦定理得false,
即false,
∴false,
即false,
所以false的周长为false.
20. 解:(1)①从统计表看出:选择理科的学生的数学平均成绩高于选择文科的学生的数学平均成绩;
②从统计数据反映了数学成绩对学生选择文理科有一定的影响.
频率分布直方图如下.
(2)设选择理科的学生考分在false,false,false分别事件false,false,false,
选择文科的学生考分在false,false,false的事件分别为false,false,false,
事件false:选取理科学生的数学成绩至少高于选取文科的学生的数学成绩一个分数段.
则false,
∴false,
由累计表可得
false.
21.(1)证明:∵false,false为false的中点,
∴false,
又平面false平面false,
平面false平面false,
∵false平面false,
又false平面false,∴false,
又false,false,
∴false平面false,
∵false平面false,∴false.
(2)∵平面false平面false,
∴false在平面false上的射影false在false上,
∴false为直线false与平面false所成的角,
解法一:
过false作false于false,连false,∵false,false,
可得false平面false,false平面false,false,
在false中,false,
在false中,false,
∴在false中,false,
∴直线false与面false所成的角的余弦值为false.
解法二:
∴false在平面false上的射影false在false上,
∴false为直线false与平面false所成的角,
在false中,false,false,
∴false为等边三角形,false,
在false中,false,∴false,
由(1)得,∴false平面false,又false平面false,
∴false,∴false,
在false中,由余弦定理得false.
22. 解:(1)在false中,∵false,
由余弦定理得false,
∴false,
(或由正弦定理得:false)
∴false,false,
∵false为等边三角形,∴false,false,
∴false,
∴false.(平方单位)
(2)不妨设false,false,false,
∴在false中,false.
在false中,由余弦定理得false,
false,
∴false,
在false中,由正弦定理得false,
∴false,
false.
当且仅当false时,等号成立.
∴false面积最大为false.(平方单位)
高一数学
注意事项:
本试卷共6页,22小题,满分150分.考试用时120分钟.
1. 答卷前,考生务必用黑色字迹钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上.
2. 选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上.
3. 作答必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液..不按以上要求作答的答案无效.
4. 考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回.
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求.
1. 设复数false(false是虚数单位),则false( )
A. false B. false C. false D. false
2. 一水平放置的平面图形,用斜二测画法画出了它的直观图,此直观图恰好是一个边长为2的正方形,则原平面图形的面积为( )
A. false B. false C. false D. false
3. 设false、false为两个互斥事件,且false,false,则下列各式错误的是( )
A. false B. false
C. false D. false
4. 已知false,false是两个不同的平面,false,false是两条不同的直线,则下列结论正确的是( )
A. 若false,false,false,则false B. 若false,false,false,则false
C. 若false,false,则false D. 若false,false,false,则false
5. 已知平面向量false,false,false与false垂直,则false的值是( )
A. -1 B. 1 C. -2 D. 2
6. 已知一组样本数据false,false,false,…,false,且false,平均数false,则该组数据的方差false( )
A. 1 B. false C. 2 D. false
7. 祖暅(公元5-6世纪,祖冲之之子),是我国齐梁时代的数学家,他提出了一条原理:“幂势既同,则积不容异.”这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现,比祖暅晚一千一百多年.椭球体是椭圆绕其轴旋转所成的旋转体.如图将底面直径皆为false,高皆为false的椭半球体和已被挖去了圆锥体的圆柱体放置于同一平面false上,以平行于平面false的平面于距平面false任意高false处可横截得到false及false两截面,可以证明false总成立.据此,短轴false长为false,长半轴false为false的椭半球体的体积是( )
A. false B. false C. false D. false
8. 已知长方体false的高false,false,false,false,则当false最大时,二面角false的余弦值为( )
A. false B. false C. false D. false
二、多项选择题:本题共4小题,每小题5分,共20 分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 已知复数false满足false(false是虚数单位),则下列关于复数false的结论正确的是( )
A. false
B. 复数false的共轭复数为false
C. 复平面内表示复数false的点位于第三象限
D. 复数false是方程false的一个根
10. 已知false的内角false,false,false所对边的长分别为false,false,false,false,false,false,若满足条件的false有两个,则false的值可以是( )
A. false B. false C. 3 D. 4
11. 在疫情防护知识竞赛中,对某校2000名考生的参赛成绩进行统计,可得到如图所示的频率分布直方图,其中分组的区间为false,false,false,false,false,false,60分以下视为不及格,若同一组中数据用该组区间中间值作代表值,则下列说法中正确的是( )
A. 成绩在false的考生人数最多
B. 不及格的考生人数为500
C. 考生竞赛成绩的众数为75分
D. 考生竞赛成绩的中位数约为75分
12. 正方体false中,false是棱false的中点,false在侧面false上运动,且满足false平面false.以下命题正确的有( )
A. 侧面false上存在点false,使得false
B. 直线false与直线false所成角可能为false
C. 平面false与平面false所成锐二面角的正切值为false
D. 设正方体棱长为1,则过点false,false,false的平面截正方体所得的截面面积的最大值为false
三、填空题:本题共4小题,每题5分,共 20分.
13. 向量false,false满足false,false,false与false的夹角为false,则false__________.
14. 某校为了普及“创建文明城市”知识,举行了一次知识竞赛,满分10分,有10名同学代表班级参加比赛,已知学生得分均为整数,比赛结束后统计这10名同学得分情况如折线图所示,则这10名同学成绩的极差为__________,false分位数是___________.
15. 梅州一所中学的高一,高二,高三的模联社团的人数分别为25,15,10,现采用分层抽样的方法从中抽取部分学生参加模联会议,已知在高二年级和高三年级中共抽取5名同学,若从这5名同学中再随机抽取2名同学承担文件翻译工作,则抽取的两名同学来自同一年级的概率为__________.
16. 在边长为3的菱形false中,false,将菱形false沿其对角线false折成直二面角false,若false,false,false,false四点均在某球面上,则该球的表面积为___________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17. 在三角形false中,false,false,false,false是线段false上一点,且false,false为线段false的中点.
(1)若false,求false的值;
(2)求false的值.
18. 如图,在正方体false中,棱长为1,false为false的中点,false.
(1)求证:false平面false;
(2)求证:false平面false;
(3)求三棱锥false的体积.
19. 在①false;②false;③false这三个条件中任选一个,补充在下面问题中,然后解答补充完整的题目.
在false中,内角false,false,false的对边分别为false,false,false,且____________________.
(1)求角false;
(2)若false,false的面积为false,求false的周长.
(注:如果选择多个条件分别解答,按第一个解答计分)
20. 我市某校为了解高一新生对文理科的选择,对1000名高一新生发放文理科选择调查表,统计知,有600名学生选择理科,400名学生选择文科.分别从选择理科和文科的学生中随机各抽取20名学生的数学成绩得如下累计表:
分数段
理科人数
文科人数
false
false
false
false
false
false
(1)利用统计表数据分析:选择文理科学生的数学平均分及数学成绩对学生选择文理科的影响;并绘制选择理科的学生的数学成绩的频率分布直方图;
(2)从数学成绩不低于70分的选择理科和文科的学生中各取一名学生的数学成绩,求选取理科学生的数学成绩至少高于选取文科学生的数学成绩一个分数段的概率.
21. 如图,在三棱柱false中,平面false底面false,false,false,false,false,false为false的中点,侧棱false.
(1)求证:false;
(2)求直线false与平面false所成角的余弦值.
22. 芹洋湿地公园是以水为主题的公园,以湿地良好生态环境和多样化湿地景观资源为基础的生态型主题公园.欲在该公园内搭建一个形状为平面凸四边形false的休闲、观光及科普宣教的平台,如图所示,其中false(单位:百米),false(单位:百米),false为正三角形.建成后false将作为人们旅游观光、休闲娱乐的区域,false将作为科普宣教湿地功能利用、弘扬湿地文化的区域.
(1)当false时,求旅游观光、休闲娱乐的区域false的面积;
(2)求旅游观光、休闲娱乐的区域false面积的最大值.
梅州市高中期末考试试卷(2021.7)
高一数学参考答案与评分意见
一、单项选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1-5:CABDA 6-8:DAB
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9. ABD 10. BC 11. AC 12. AC
三、填空题:本大题共4小题,每小题5分,满分20分.
13. false 14. 7,8.5 15. false 16. false
四、解答题:本大题共6小题,满分70分.解答须写出文字说明,证明过程或演算步骤.
17. 解:(1)∵false,∴false,
得false,
∵false,∴false,false,
∴false.
(2)∵在三角形false中,false,false,false,
∴false,false,
∵false,∴false为等边三角形,
∴false.
18.(1)证明:∵在正方体中,false平面false,
false平面false,∴false,
∵false,false,
∴false平面false.
(2)证明:连接false,
∵在正方体中,false且false,
∴四边形false是平行四边形,
∴false且false,
∵false,false分别为false,false中点,∴false,
∴四边形false是平行四边形,
∴false,
∵false平面false,false平面false,
∴false平面false.
(3)由(2)得false平面false,
∴false点到平面false的距离即为false点到平面false的距离,
∴false
false
false.
19. 解:(1)选①,∵false,
∴由正弦定理得false,
即false,
又在false中,false,false,false,
∴false,
∴false,
∵false,
∴false.
选②,∵false,
∴由正弦定理得false,
又在false中,false,false,
∴false,
∵false,
∴false.
选③,∵false,
∴false,即false,
∴由余弦定理得false,
∵false,
∴false.
(2)∵false,false,false的面积为false,
∴false,
∴false,
又由余弦定理得false,
即false,
∴false,
即false,
所以false的周长为false.
20. 解:(1)①从统计表看出:选择理科的学生的数学平均成绩高于选择文科的学生的数学平均成绩;
②从统计数据反映了数学成绩对学生选择文理科有一定的影响.
频率分布直方图如下.
(2)设选择理科的学生考分在false,false,false分别事件false,false,false,
选择文科的学生考分在false,false,false的事件分别为false,false,false,
事件false:选取理科学生的数学成绩至少高于选取文科的学生的数学成绩一个分数段.
则false,
∴false,
由累计表可得
false.
21.(1)证明:∵false,false为false的中点,
∴false,
又平面false平面false,
平面false平面false,
∵false平面false,
又false平面false,∴false,
又false,false,
∴false平面false,
∵false平面false,∴false.
(2)∵平面false平面false,
∴false在平面false上的射影false在false上,
∴false为直线false与平面false所成的角,
解法一:
过false作false于false,连false,∵false,false,
可得false平面false,false平面false,false,
在false中,false,
在false中,false,
∴在false中,false,
∴直线false与面false所成的角的余弦值为false.
解法二:
∴false在平面false上的射影false在false上,
∴false为直线false与平面false所成的角,
在false中,false,false,
∴false为等边三角形,false,
在false中,false,∴false,
由(1)得,∴false平面false,又false平面false,
∴false,∴false,
在false中,由余弦定理得false.
22. 解:(1)在false中,∵false,
由余弦定理得false,
∴false,
(或由正弦定理得:false)
∴false,false,
∵false为等边三角形,∴false,false,
∴false,
∴false.(平方单位)
(2)不妨设false,false,false,
∴在false中,false.
在false中,由余弦定理得false,
false,
∴false,
在false中,由正弦定理得false,
∴false,
false.
当且仅当false时,等号成立.
∴false面积最大为false.(平方单位)
同课章节目录
