七年级数学一元一次不等式的性质
文档属性
| 名称 | 七年级数学一元一次不等式的性质 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-29 00:00:00 | ||
图片预览








文档简介
(共29张PPT)
复习回顾
一.等式的性质
等式的基本性质1:在等式两边都加上(或减去)同一个数或整式,结果仍相等.
等式的基本性质2:在等式两边都乘以或除以同一个数(除数不为0),结果仍相等.
二.解一元一次方程的基本步骤
1.去分母
2.去括号
3. 移项
4. 合并同类项
5. 系数化为1
第一关 智力比拼
有一个公安局退休老局长和一个中年人
在街上遇见一个过路人,
路人问局长:“这是你的儿子吗?”局长说:“是。”
他又问中年人:“这是你父亲吗?”
中年人说:“不是。”请问怎么回事
如果妈妈今年70岁,儿子今年40岁,怎么用不等式来表示妈妈和儿子的年龄大小关系呢?
70﹥40
70+5﹥40+5
70 - 30﹥40 - 30
70 - x﹥40 - x
不等式的性质1 不等式的两边加(或减)同一个数(或式子),不等号的方向不变.
等式的性质1 等式的两边加上(或减去)同一个数(或式子),结果仍相等。
不等式的性质1 不等式的两边加(或减)同一个数(或式子),不等号的方向不变.
如果a>b,那么a±c b±c
符号语言表示为:
﹥
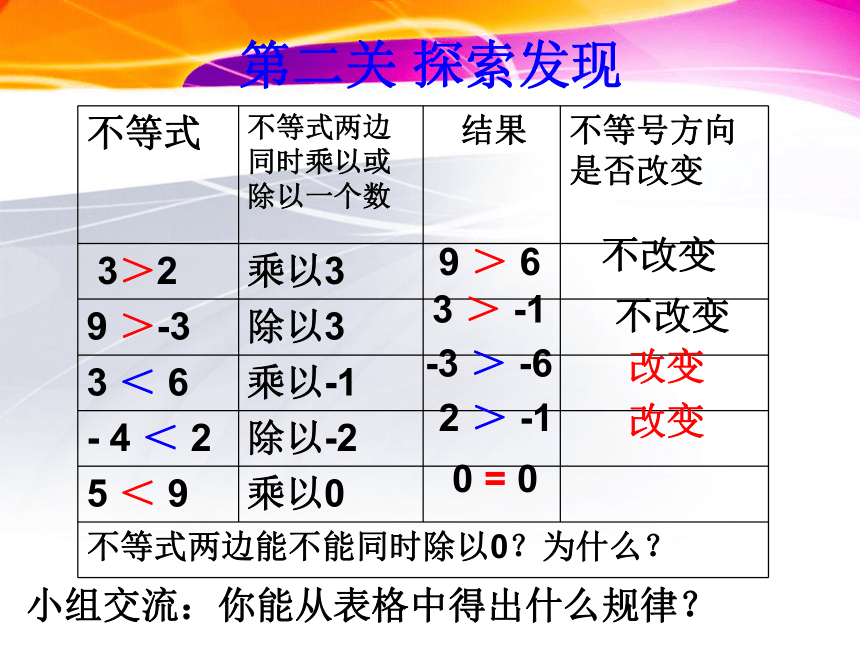
不等式 不等式两边同时乘以或除以一个数 结果
不等号方向是否改变
3>2 乘以3
9 >-3 除以3
3 < 6 乘以-1
- 4 < 2 除以-2
5 < 9 乘以0
不等式两边能不能同时除以0?为什么?
9 > 6
3 > -1
-3 > -6
2 > -1
0 = 0
不改变
改变
改变
不改变
第二关 探索发现
小组交流:你能从表格中得出什么规律?
不等式的性质2 不等式的两边乘(或除以)同一个正数,不等号的方向不变.
如果a>b,c>0那么ac bc,
>
>
不等式的性质 3 不等式的两边乘(或除以)同一个负数,不等号的方向改变
如果a>b,c<0那么ac ﹤ bc,
﹤
不等式的性质1 不等式的两边加(或减)同一个数(或式子),不等号的方向不变.
不等式的性质2 不等式的两边乘(或除以)同
一个正数,不等号的方向不变.
不等式的性质 3 不等式的两边乘(或除以)
同一个负数,不等号的方向改变
练习1
选择适当的不等号,并说明利用不等式那条性质.
1.已知a>b,则a+1 b+1.
2.已知a>b,则2a 2b.
3.已知a>b,则-3a -3b.
4. 若a<b,则a-1____b-1 .
>
>
<
(不等式基本性质1)
(不等式基本性质2)
(不等式基本性质3)
(不等式基本性质1)
<
第三关 小试牛刀
巧记口诀
加减都用性质1,不等号方向不改变。
乘除正数性质2,不等号方向还不变。
乘除负数性质3,不等号方向必改变。
练习2 判断正误并说明理由
1、已知a+m>b+m,可得a>b
2、已知- 4x<- 4y,可得x<y
3、已知2a+1>2b+1,可得a>b
4、已知a>b,可得 ac >bc
5、已知5>4,可得5a>4a
( × )
( √ )
( × )
( × )
( √ )
练习3:
用“>”或“<”在横线上填空.
已知x+4>5,根据不等式性质______,不等式
两边同时____________得到 x____1.
(2)已知2x<4,根据不等式性质______,不等式
两边同时____________得到 x____2.
(3)已知a-3<8,根据不等式性质______,不等式两边同时____________得到 a____11.
1
减去2
除以2
加上3
>
<
<
2
1
(4)已知 ,根据不等式性质______,
不等式两边同时_________,得到 x____10.
(5)已知4x>3x-1 ,根据不等式性质______,
不等式两边同时_________,得到 x____-1.
减去3x
>
>
3
1
例1 利用不等式的性质解下列不等式.
(1) x-7>26 (2) 3x<2x+1
(3) - x﹥50 (4) -4x﹥3
3
2
我是最棒的
(1) x-7>26
分析:解未知数为x的不等式,就是要使不等式逐步化为x﹥a或x﹤a的形式.
解:(1)根据不等式的性质1,不等式两边都加7得
x-7+7﹥26+7
x﹥33
这个不等式的解集在数轴上的表示如图,
锋 芒 初 试
0
33
(2) 3x<2x+1
3x-2x﹤2x+1-2x x﹤1
根据 ,不等式两边都减去 ,不等号得
这个不等式的解在数轴上的表示如图
注意:解不等式时也可以“移项”,即把不等式的一边的某项变号后移到另一边,而不改变不等号的方向.
言必有“据”
0
1
2
(3) - x﹥50
3
2
为了使不等式- x﹥50中不等号的一边变为x,根据不等式的性质2,不等式的两边都乘 不等号的方向不变,得
3
3
2
x﹥75
这个不等式的解集在数轴的表示如图
言必有“据”
0
75
(4) -4x﹥3
为了使不等式-4x﹥3中的不等号的一边变为x,根据 ,不等式两边都除以 ,不等号的方向 ,得
x﹤-
4
3
这个不等式的解集在数轴上的表示如图
注意:(3)(4)的求解过程,类似于解方程两边都除以未知数的系数(未知数系数化为1),解不等式时要注意未知数系数的正负,以决定是否改变不等号的方向
言必有“据”
-
4
3
0
第四关 乘胜追击
例题把下列不等式化成x<a或x>a的形式,并把解集在数轴上表示出来
-2x - 3>2
即x< -2.5
解:根据不等式性质1,两边同时加3
-2x – 3+3>2+3 即-2x >5
根据不等式性质3,两边同时除以-2
针对练习 ( 1)3x+1<7 (2) - 4x - 5﹥3
第五关 勇攀高峰
如图:
a
b
0
c
用“>”或“<”在横线上填空
1、a+c_______b+c
2、ac________bc
练习
若x≠2,且a(x - 2)>b(x - 2)
试比较a与b的大小
解:当x>2,则x - 2>0,
把不等式两边同时除以x - 2,
根据不等式性质2
得到a>b。
当x<2,则x - 2<0,
把不等式两边同时除以x - 2,
根据不等式性质3
得到a<b。
本节课的收获
1、不等式的性质1 不等式的两边加(或减)同一个数(或式子),不等号的方向不变.
2、不等式的性质2 不等式的两边乘(或除以)同一个正数,不等号的方向不变.
3、不等式的性质 3 不等式的两边乘(或除以)同一个负数,不等号的方向改变
三种数学思想方法
1、数形结合思想
2、类比思想
3、分类讨论思想
作 业:
配套练习册
若x>y,则ax>ay.那么一定有( )
A、a>0 B、a≥0 C、a<0 D、a≤0
已知关于x的不等式(1-a)x>2的解集是
x< ,则a的取值范围( )
A、a>0 B、a>1
C、a<0 D、a<1
课堂检测
1、已知a<b,下列式子中,错误的是( )
A、4a<4b B、-4a<-4b C.、a+4<b+4 D、a-4<b-4
2、.已知x<y,用“<”或“>”号填空。
(1); (2); (3); (4)
根据不等式的性质,将不等式变形成x>a或x<a的形式。
(1)x>-3; (2)-2x<3x+5
复习回顾
一.等式的性质
等式的基本性质1:在等式两边都加上(或减去)同一个数或整式,结果仍相等.
等式的基本性质2:在等式两边都乘以或除以同一个数(除数不为0),结果仍相等.
二.解一元一次方程的基本步骤
1.去分母
2.去括号
3. 移项
4. 合并同类项
5. 系数化为1
第一关 智力比拼
有一个公安局退休老局长和一个中年人
在街上遇见一个过路人,
路人问局长:“这是你的儿子吗?”局长说:“是。”
他又问中年人:“这是你父亲吗?”
中年人说:“不是。”请问怎么回事
如果妈妈今年70岁,儿子今年40岁,怎么用不等式来表示妈妈和儿子的年龄大小关系呢?
70﹥40
70+5﹥40+5
70 - 30﹥40 - 30
70 - x﹥40 - x
不等式的性质1 不等式的两边加(或减)同一个数(或式子),不等号的方向不变.
等式的性质1 等式的两边加上(或减去)同一个数(或式子),结果仍相等。
不等式的性质1 不等式的两边加(或减)同一个数(或式子),不等号的方向不变.
如果a>b,那么a±c b±c
符号语言表示为:
﹥
不等式 不等式两边同时乘以或除以一个数 结果
不等号方向是否改变
3>2 乘以3
9 >-3 除以3
3 < 6 乘以-1
- 4 < 2 除以-2
5 < 9 乘以0
不等式两边能不能同时除以0?为什么?
9 > 6
3 > -1
-3 > -6
2 > -1
0 = 0
不改变
改变
改变
不改变
第二关 探索发现
小组交流:你能从表格中得出什么规律?
不等式的性质2 不等式的两边乘(或除以)同一个正数,不等号的方向不变.
如果a>b,c>0那么ac bc,
>
>
不等式的性质 3 不等式的两边乘(或除以)同一个负数,不等号的方向改变
如果a>b,c<0那么ac ﹤ bc,
﹤
不等式的性质1 不等式的两边加(或减)同一个数(或式子),不等号的方向不变.
不等式的性质2 不等式的两边乘(或除以)同
一个正数,不等号的方向不变.
不等式的性质 3 不等式的两边乘(或除以)
同一个负数,不等号的方向改变
练习1
选择适当的不等号,并说明利用不等式那条性质.
1.已知a>b,则a+1 b+1.
2.已知a>b,则2a 2b.
3.已知a>b,则-3a -3b.
4. 若a<b,则a-1____b-1 .
>
>
<
(不等式基本性质1)
(不等式基本性质2)
(不等式基本性质3)
(不等式基本性质1)
<
第三关 小试牛刀
巧记口诀
加减都用性质1,不等号方向不改变。
乘除正数性质2,不等号方向还不变。
乘除负数性质3,不等号方向必改变。
练习2 判断正误并说明理由
1、已知a+m>b+m,可得a>b
2、已知- 4x<- 4y,可得x<y
3、已知2a+1>2b+1,可得a>b
4、已知a>b,可得 ac >bc
5、已知5>4,可得5a>4a
( × )
( √ )
( × )
( × )
( √ )
练习3:
用“>”或“<”在横线上填空.
已知x+4>5,根据不等式性质______,不等式
两边同时____________得到 x____1.
(2)已知2x<4,根据不等式性质______,不等式
两边同时____________得到 x____2.
(3)已知a-3<8,根据不等式性质______,不等式两边同时____________得到 a____11.
1
减去2
除以2
加上3
>
<
<
2
1
(4)已知 ,根据不等式性质______,
不等式两边同时_________,得到 x____10.
(5)已知4x>3x-1 ,根据不等式性质______,
不等式两边同时_________,得到 x____-1.
减去3x
>
>
3
1
例1 利用不等式的性质解下列不等式.
(1) x-7>26 (2) 3x<2x+1
(3) - x﹥50 (4) -4x﹥3
3
2
我是最棒的
(1) x-7>26
分析:解未知数为x的不等式,就是要使不等式逐步化为x﹥a或x﹤a的形式.
解:(1)根据不等式的性质1,不等式两边都加7得
x-7+7﹥26+7
x﹥33
这个不等式的解集在数轴上的表示如图,
锋 芒 初 试
0
33
(2) 3x<2x+1
3x-2x﹤2x+1-2x x﹤1
根据 ,不等式两边都减去 ,不等号得
这个不等式的解在数轴上的表示如图
注意:解不等式时也可以“移项”,即把不等式的一边的某项变号后移到另一边,而不改变不等号的方向.
言必有“据”
0
1
2
(3) - x﹥50
3
2
为了使不等式- x﹥50中不等号的一边变为x,根据不等式的性质2,不等式的两边都乘 不等号的方向不变,得
3
3
2
x﹥75
这个不等式的解集在数轴的表示如图
言必有“据”
0
75
(4) -4x﹥3
为了使不等式-4x﹥3中的不等号的一边变为x,根据 ,不等式两边都除以 ,不等号的方向 ,得
x﹤-
4
3
这个不等式的解集在数轴上的表示如图
注意:(3)(4)的求解过程,类似于解方程两边都除以未知数的系数(未知数系数化为1),解不等式时要注意未知数系数的正负,以决定是否改变不等号的方向
言必有“据”
-
4
3
0
第四关 乘胜追击
例题把下列不等式化成x<a或x>a的形式,并把解集在数轴上表示出来
-2x - 3>2
即x< -2.5
解:根据不等式性质1,两边同时加3
-2x – 3+3>2+3 即-2x >5
根据不等式性质3,两边同时除以-2
针对练习 ( 1)3x+1<7 (2) - 4x - 5﹥3
第五关 勇攀高峰
如图:
a
b
0
c
用“>”或“<”在横线上填空
1、a+c_______b+c
2、ac________bc
练习
若x≠2,且a(x - 2)>b(x - 2)
试比较a与b的大小
解:当x>2,则x - 2>0,
把不等式两边同时除以x - 2,
根据不等式性质2
得到a>b。
当x<2,则x - 2<0,
把不等式两边同时除以x - 2,
根据不等式性质3
得到a<b。
本节课的收获
1、不等式的性质1 不等式的两边加(或减)同一个数(或式子),不等号的方向不变.
2、不等式的性质2 不等式的两边乘(或除以)同一个正数,不等号的方向不变.
3、不等式的性质 3 不等式的两边乘(或除以)同一个负数,不等号的方向改变
三种数学思想方法
1、数形结合思想
2、类比思想
3、分类讨论思想
作 业:
配套练习册
若x>y,则ax>ay.那么一定有( )
A、a>0 B、a≥0 C、a<0 D、a≤0
已知关于x的不等式(1-a)x>2的解集是
x< ,则a的取值范围( )
A、a>0 B、a>1
C、a<0 D、a<1
课堂检测
1、已知a<b,下列式子中,错误的是( )
A、4a<4b B、-4a<-4b C.、a+4<b+4 D、a-4<b-4
2、.已知x<y,用“<”或“>”号填空。
(1); (2); (3); (4)
根据不等式的性质,将不等式变形成x>a或x<a的形式。
(1)x>-3; (2)-2x<3x+5
